Метод конечных разностей (МКР)
Основные понятия
МКР, или метод сеток, в настоящее время является одним из наиболее распространенных методов приближенного решения краевых задач.
Суть метода в следующем:
1. Область непрерывного изменения аргумента (отрезок, прямоугольник и т.д.) заменяется конечным (дискретным) множеством точек (узлов), называемым сеткой.
2. Вместо функции непрерывного изменения аргумента рассматриваются функции дискретного аргумента, определенные в узлах сетки и называемые сеточными функциями.
3. Производные, входящие в дифференциальные уравнения и краевые условия, заменяются (аппроксимируются) разностными соотношениями, т.е. линейными комбинациями значений сеточных функций в некоторых узлах сетки.
4. В результате краевая задача для дифференциального уравнения заменяется системой линейных, если исходная задача была линейной, алгебраических уравнений – разностной схемой.
Если, полученная таким образом задача разрешима и ее решение при измельчении сетки приближается (сходится) к решению исходной задачи для дифференциального уравнения, то оно и принимается за приближенное решение исходной задачи.
Несмотря на внешнюю простоту метода, прежде, чем приступить к решению конкретной задачи, необходимо уметь дать ответы на следующие вопросы:
1) как выбрать сетку?
2) Как написать разностную схему?
3) Насколько хорошо разностная схема аппроксимирует исходную задачу?
4) Устойчива ли разностная схема и в каком смысле?
5) Какова скорость сходимости решения разностной задачи к решению исходной задачи?
Сетки и сеточные функции
Свойства разностного решения и, в частности, его близость к точному решению зависит от выбора сетки. Расположение узлов сетки в области может быть произвольным и определяться спецификой решаемой задачи. Рассмотрим несколько примеров
1) равномерная сетка на отрезке
2) неравномерная сетка на отрезке
Рассмотрим тот же отрезок 
. Введя произвольные точки 
, разобьем его на N частей. Тогда получим сетку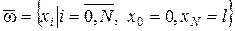 
с шагом 
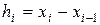, который зависит от номера i узла 
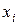. Если 
хотя бы для одного номера i, то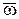 
- неравномерная сетка.
Очевидно, что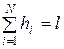 
.
3) равномерная сетка на плоскости
Рассмотрим множество функций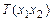 
двух аргументов. В качестве области определения выберем прямоугольник
,
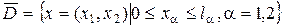например,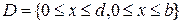 
Построим на каждом отрезке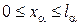 
сетку 
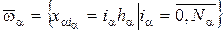с шагом 
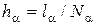. Множество узлов 
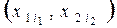с координатами 
(
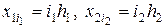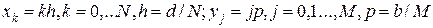) назовем сеткой в прямоугольнике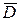 
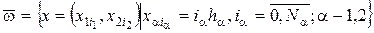
Эта сетка равномерна по каждому из переменных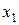 
и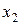 
. Если хотя бы одна из сеток 
неравномерна, то сетка 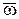называется неравномерной. Если 
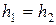, то сетка называется квадратной, 
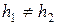- прямоугольной.
4) сетка на плоскости в произвольной области
Пусть на плоскости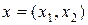 
дана область G сложной формы с границей Г. Проведем прямые
Тогда на плоскости получим сетку с узлами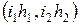 
, 
. Эта сетка равномерна по каждому направлению. Нас интересуют только те узлы, которые принадлежат области G с границей Г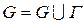 
.
Узлы, попавшие внутрь G, назовем внутренними узлами и обозначим их совокупность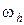 
. Точки пересечения прямых 
с границей Г назовем граничными узлами, а их множество обозначим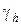 
. Видно, что имеются граничные узлы, которые отстоят от ближайших к ним внутренних узлов на расстояния меньшем 
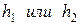. Таким образом, сетка 
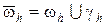для области G неравномерна вблизи границы.
Построение разностной схемы проводится таким образом, чтобы получаемая в результате решения сеточная функция была как можно ближе к искомой непрерывной функции.
Вместо функций 
непрерывного аргумента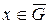 
будем рассматривать сеточные функции 
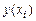, т.е. функции точки 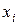, являющейся узлом сетки 
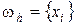в виде вектора 
.
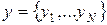Для оценки близости приближенного решения (решения на сетке) к точному решению исходной краевой задачи можно использовать два способа
1. Производится интерполяция сеточной функции на все точки области G, после чего определяется норма разности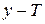 
.
2. Точное решение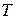 
преобразуется в сеточную функцию 
(
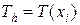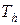- одно из возможных обозначений сеточных функций), после чего, определив сеточную норму 
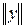, оценивается погрешность приближенного решения в этой норме. На практике в качестве сеточных норм используются:
а) сеточный аналог чебышевской нормы в пространстве непрерывных функций С 
б) сеточный аналог гильбертовой нормы в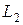 
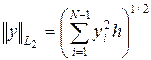, где h=h в одномерном случае и 
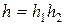в двумерном.
Тогда если при бесконечном дроблении сетки величина 
, то можно говорить о близости решения разностной и краевой задачи.