ПОДБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ ПО ОПЫТНЫМ ДАННЫМ И ПРОВЕРКА ЕГО СОГЛАСИЯ ПО КРИТЕРИЮ 
Задание для расчётно-графической работы.
I. Из приложения 1 или 2 взять выборку объёма n=150. Выборку произвести с использованием таблиц случайных чисел приложении 4 (или каким – либо другим методом, указанным преподавателем). Варианты индивидуальных заданий даны в приложении 3.
2. По выборке найти статические оценки математического ожидания и среднего квадратичного отклонения (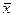
и S).
3. Построить гистограмму.
4. Подобрать закон распределения случайной величины (например: нормальный, показательный, равномерный).
5. Проверить согласие закона распределения с опытными данными по критерию 
при уровне значимости 
.
6. Теоретическую кривую нанести на гистограмму опытных данных.
Методические указания к выполнению расчётно–графической работы.
1. Упорядочить выборку по возрастанию, найти 
2.Весь интервал, в который попали опытные данные, разбить на r частичных интервалов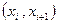 
. При выборе длины частичных интервалов рекомендуется формула
. (1)
За шаг h принимается некоторое удобное число, ближайшее к значению 
Для удобства границы интервалов выбираются так, чтобы результаты измерений не совпали с границами интервалов.
Начало первого интервала сдвинуть влево от значения 
(например, взять - 0,5).
3. Для каждого частичного интервала 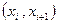найти 
сумму частот вариант и считать, что 
сосредоточено в середине i – ого интервала, т.е. взять 
4. Построить гистограмму частот. По виду гистограммы подобрать закон распределения случайной величины.
5. По выборке найти:
6. Найти теоретические частоты 
, попавшие в i – ый интервал по формуле
, (4)
где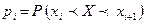 
.
Если случайная величина распределена по нормальному закону, то
, (5)
где 
Таблица значений функции Ф(x) приведена в приложении 4.
Если случайная величина распределена по закону Пуассона, то
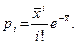(6)
7. Вычислить наблюдаемое значение критерия 
по формуле
(7)
где r – число интервалов, 
- эмпирическая частота i - ого интервала, - теоретическая частота i - ого интервала.
8. По таблице 
- распределения на уровне значимости 
и числе степеней свободы k найти критическое значение 
(приложение 3).
Число степеней свободы k находится по формуле
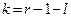, (8)
где r – число частичных интервалов, l – число параметров предполагаемого распределения, которые оценены по данным выборки.
В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение), поэтому l =2. Если предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр 
, поэтому l =1.
9. Сравнить два значения и . Если 
, то нулевая гипотеза не отвергается, т.е. в этом случае отклонения от предполагаемого теоретического закона считаются незначительными. Если 
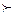
, то нулевая гипотеза отвергается.
Замечание. Малочисленные частоты ( 
5) следует объединить. При определении числа степеней свободы в качестве r следует принять число групп выборки, оставшихся после объединения частот.
Пример.
Контролировался диаметр у 150 цапф передней оси, изготовленных на токарном станке. В результате были получены значения положительных отклонений в микронах (мк) от номинального размера 20 мк:
.
Проверить согласие нормального закона распределения с опытными данными по критерию при уровне значимости .
Решение
1. Случайную величину обозначим X. Находим:
Возьмём h = 3мк. Левый конец первого интервала возьмём 24,5мк. Из приведённых значений найдём число опытных данных, попавших в каждый частичный интервал.
Полученные данные сведём в таблицу 1.
Таблица 1
| i | 
| 
| i |
|
|
| 24,5 - 27,5 | 39,5 - 42,5 | ||||
| 27,5 - 30,5 | 42,5 - 45,5 | ||||
| 30,5 - 33,5 | 45,5 - 48,5 | ||||
| 33,5 - 36,5 | 48,5 - 51,5 | ||||
| 36,5 - 39,5 | 51,5 - 54,5 |
2. построим гистограмму частот (рис1).
Рис. 1
3. Для каждого частичного интервала найдем 
. Вычислим значения 
и S по формулам (2) и (3).
Для удобства вычислений необходимые расчеты поместим в таблицу 2
.
Таблица 2
| i | 
| 
| 
| 
| 
| 
|
| 24,5-27,5 | ||||||
| 27,5-30,5 | ||||||
| 30,5-33,5 | ||||||
| 33,5-36,5 | ||||||
| 36,5-39,5 | ||||||
| 39,5-42,5 | ||||||
| 42,5-45,5 | ||||||
| 45,5-48,5 | ||||||
| 48,5-51,5 | ||||||
| 51,5-54,5 | ||||||
| ∑ |
Получаем: 
; 
S=5,8.
По виду гистограммы (рис.1) можно предположить, что исследуемый признак распределен нормально.
4. Найдем теоретические частоты, используя формулы (4) и (5) при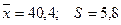 
:
.
Для первого интервала левый конец изменим на 
, а в последнем интервале правый конец изменим на +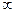 
. Таким образом, первый интервал будет 
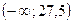, а последний - 
. Расчёт 
приведён в таблице 3.
Таблица 3
| i | 
|
|
| 
|
| 27,5
27,5 30,5
| 
| 
| 0,39 | |
| 30,5 33,5 | 11,0 | 0,36 | ||
| 33,5 36,5 | 20,2 | 0,39 | ||
| 36,5 39,5 | 27,8 | 1,21 | ||
| 39,5 42,5 | 30,6 | 0,01 | ||
| 42,5 45,5 | 24,4 | 0,88 | ||
| 45,5 48,5 | 15,4 | 0,02 | ||
48,5 51,5
51,5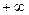  
| 
| 
| 0,00 | |
| 3,26 |
Приводим пример расчета значения :
и так далее.
5. Проверку гипотезы о нормальном распределении проводим при уровне значимости
= 0,05 и числе степеней свободы 
Из таблицы (см. приложение 3) находим 
В нашем примере 
, т.е.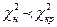 
.
Следовательно, опытные данные согласуются с нормальным законом распределения. На гистограмму наложим теоретическую кривую, полученную в соответствии с нормальным законом распределения.
6. Для построения нормальной кривой по опытным данным находят ординаты 
(выравнивающие частоты) по формуле
Значения функции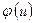 
находим в таблице приложения 5.
В прямоугольной системе координат строят точки 
и соединяют их плавной кривой.
Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что исследуемый признак распределен нормально.
Вычислим выравнивающие частоты для нашего примера. Имеем
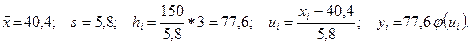
Результаты вычислений поместим в таблицу 4.
Таблица 4
| i | 
|
| 
| 
|
|
| -2,48 | 0,02 | 1,6 | |||
| -1,96 | 0,05 | 3,9 | |||
| -1,45 | 0,14 | 10,8 | |||
| -0,94 | 0,26 | 20,2 | |||
| -0,41 | 0,37 | 28,7 | |||
| 0,10 | 0,39 | 30,3 | |||
| 0,62 | 0,33 | 25,6 | |||
| 1,14 | 0,21 | 16,3 | |||
| 1,66 | 0,09 | 7,0 | |||
| 2,17 | 0,04 | 3,1 |
ПРИЛОЖЕНИЕ 1
| Долговечность деталей, час | Время | час | |||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Продолжение таблицы приложения 1 | Время | час | |||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Время | час | ||||||||||||||||||||||||||||||||||||||||||||||||
| № | п/п | ||||||||||||||||||||||||||||||||||||||||||||||||
| Продолжение таблицы приложения 1 | Время | час | ||||||||||||||||||||||
| № | п/п | .399 | ||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п |
| Продолжение таблицы приложения 1 | Время | час | ||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Окончание таблицы приложения 1 | Время | час | ||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||
| № | п/п |
ПРИЛОЖЕНИЕ 2
| Долговечность деталей, час | Время | час | ||||||||||||||||||||||||
| № | п/п | |||||||||||||||||||||||||
| Время | час | |||||||||||||||||||||||||
| № | п/п |
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-08-20 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд Интересно: |