Тест
1. Задачей курса «Математическая логика» является знакомство и освоение....................................................................................................
2. Совокупность элементов, объединенных некоторым признаком, свойством, составляют понятие..............................................................
3. Выберите правильное определение: Множество А является строгим подмножеством множества В, если:
- всякий элемент множества А является элементом множества В;
- часть элементов множества А совпадает с элементами множества В;
- множества А и В равны;
- все элементы множества А входят во множество В, но не наоборот;
5. Выберите правильное определение: Множество, мощность которого равно нулю называется
- конечным;
- бесконечным;
- пустым;
6. Определите способ задания множества
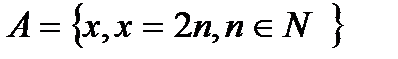
- пораждающая процедура;
- распознающая процедура;
- заданием характеристических свойств;
- рекурсивный способ задания;
- списком.
7. Какова мощность булеана на множестве М=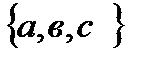 
- 8
- 12
- 10
- 9
8. Какое из приведенных определений множеств А, В, С, Д является некорректным
- 
- 
- 
- 
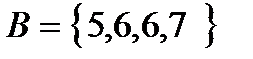
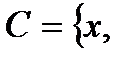
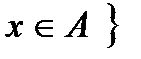
9. Установите определение, соответствующее операции над множествами
| № | Операция | № | Определение |
| Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств | ||
| Множество, состоящее из элементов, которые принадлежат обоим множествам | ||
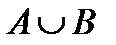
| Множество, состоящее только из элементов первого множества |
10.
| В |
| А |
| С |
Изобразите на диаграмме Венна операции над множествами 
11. Изобразите на диаграмме Венна операции над
множествами 
| А |
| С |
| В |
12. Установите соответствие между свойствами отношений и их определениями:
- 
- симметрично
- 
- транзитивно
- 
- анти рефлексивно
- 
- антисимметрично
- 
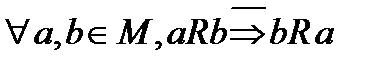- рефлексивно
13. Подчеркните те свойства, которыми обладает отношение на множестве натуральных чисел «Быть не меньше»
- рефлексивно
- анти рефлексивно
- симметрично
- антисимметрично
- транзитивно
14. Подчеркните те свойства, которыми обладает отношение
на множестве людей «Быть сыном»
- рефлексивно
- анти рефлексивно
- симметрично
- антисимметрично
- транзитивно
15. Подчеркните те свойства, которыми обладает отношение
на множестве элементов ПК «Быть помощником»
- рефлексивно
- анти рефлексивно
- симметрично
- антисимметрично
- транзитивно
16. Вставьте пропущенные слова в определение:
Соответствие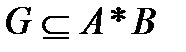 
называется всюду определенным, если множество всех его...................................... совпадает со множеством....
17. Вставьте пропущенные слова в определение:
Соответствие 
называется сюрьективным, если множество всех его................................... совпадает со множеством......
18. Вставьте пропущенные слова в определение:
Соответствие называется функциональным, если каждому его.......................... соответствует единственный.............................
19. Перечислите свойства взаимно-однозначного соответствия
1..................................................
2..................................................
3..................................................
4..................................................
20. Множества, равномощные множеству натуральных чисел
называются..........................
21. Множества, равномощные множеству действительных чисел
называются............................
22. G – соответствие. Найдите пр12=
пр14= пр25=
пр1 
= пр2 
=
пр23=
| G |
23. Подчеркните свойства, которыми обладает соответствие G:
- всюду определено
- сюрьективно
- функционально
- взаимно-однозначно
24. Подчеркните свойства, которыми обладает соответствие G:
- всюду определено
- сюрьективно
- функционально
- взаимно-однозначно
25. Подчеркните свойства, которыми обладает соответствие G:
- всюду определено
- сюрьективно
- функционально
- взаимно-однозначно
26. Даны функции 
f(x)=2x, g(x)=3x+2, p(x)=tgx.
Чему равна композиция h=f(p(g(x)))=
27. Высказывание называется простым, если оно................................................
.............................................................................................................................
28. Высказывание называется сложным, если оно...............................................
.............................................................................................................................
29. Конъюнкцией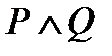 
называется высказывание............., если первое............, второе..................
30. Дизъюнкцией 
называется высказывание.................., если первое............, второе.................
31. Инверсией называется высказывание................., если само высказывание
.......................
32. Импликацией 
называется высказывание..................., если первое высказывание..................., а второе.......................
33. Эквивалентностью называется высказывание......................., если оба высказывания............................... или.............................
34. Неравнозначностью называется высказывание...................., если одно высказывание......................., а второе............................
35. Формула 
:
- просто выполнима
- тождественно истинна
- тождественно ложна
36. Формула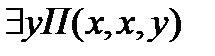 
:
- просто выполнима
- тождественно истинна
- тождественно ложна
37. Формула 
:
- просто выполнима
- тождественно истинна
- тождественно ложна
38. Формула 
:
- просто выполнима
- тождественно истинна
- тождественно ложна
39. Формула 
:
- просто выполнима
- тождественно истинна
- тождественно ложна
40. Определите разделимую схему алфавитного кодирования:
- 
- 
- 
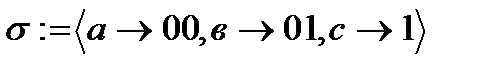
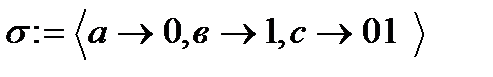
41. Определите закрытый ключ при следующих условиях генерации открытого ключа:
p=3; q=17 и е=5
- d=17
- d=13
- d=11
- d=9
-
42. Определите закрытый ключ при следующих условиях генерации открытого ключа:
p=7; q=5 и е=5
- d=7
- d=9
- d=5
- d=3
43. Определите закрытый ключ при следующих условиях генерации открытого ключа:
p=5; q=13 и e=7
- d=5
- d=9
- d=11
- d=7
44. Выберите соответствующий вид графа:
- н-граф
- ор-граф
- полный
- мультиграф
- полностью задан
45. Определите сумму степеней вершин графа:
- 6
- 5
- 4
- 7
46. Определите сумму степеней вершин графа:
- 12
- 14
- 16
- 18
:
47. Перечислите способы задания графа:
1. _______________________________
2. _______________________________
3. _______________________________
48. Какие из понятий графа являются его частями:
- мультиграф
- суграф
- подграф
- полный граф
- покрывающий граф
49. Каким свойством обладает ор-граф, если он не содержит кратных ребер?
____________________________________________________
50. Каким свойством обладает н-граф, если все его вершины содержат петли?
___________________________________________________
51. Подчеркните свойства, которыми обладает n-граф, заданный матрицей смежности:
- рефлексивен
| G | a | b | c | d | e |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
- анти рефлексивен
- симметричен
- анти симметричен
- транзитивен
52. Маршрут, в котором совпадают начало и конец называется ______________
53. Цепь, не пересекающая себя в вершинах называется _______________
54. Если существует маршрут с началом в V1 и концом V2, то эти вершины называются __________________________
55. Контур – это путь в котором ____________________
56. Длиной маршрута называется ___________________________________
57. Расстоянием от вершины V1 до вершины V2 называется ___________________________________________________________________________________________________________________________________
58. Центром n-графа называется его вершина, от которой _______________
расстояние до других вершин являлось бы ______________________
59. Радиусом графа называется ____________________ расстояние от его
____________________ до его ________________________
60. Установите соответствие понятия комбинаторики и его формулы:
1.Размещения без повтора 
2.Размещения с повторением 
3.Сочетания без повтора nm
4.Сочетания с повторением 
5.Перестановки 
61. Составьте 8-ой ряд треугольника Паскаля и возведите в степень
(a-b)7=_________________________________________________________
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
62. Принцип математической индукции заключается в следующем:
1. Р(n) – истинно для___________________
2. Пусть Р(n) –истинно для ____________
3. Доказать, что Р(n) истинно и для ___________
63. Если прямая теорема сформулирована в виде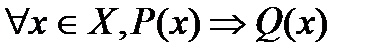 
, то теорема 
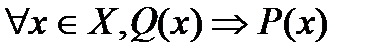называется___________________________
64. Если прямая теорема сформулирована в виде 
, то теорема 
называется ___________________________
65. Если прямая теорема сформулирована в виде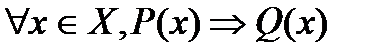 
, то теорема 
называется _________________________________