Объём цилиндра можно рассчитать по формуле:
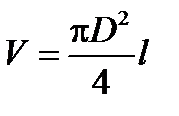 ,
,
где D – диаметр, l – длина, измеряемые прямым образом.
Выведем формулу погрешности косвенного измерения объёма. Для этого воспользуемся формулой (12), которая в нашем частном случае приобретает вид
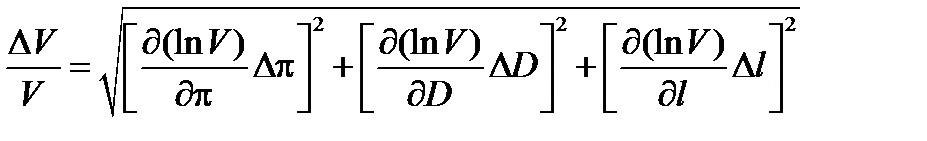 .
.
В расчёте p всегда имеет приближённое значение, а значит, имеет место ошибка округления Dp и её следует учитывать. Таким образом, чтобы определить относительную погрешность D V / V, необходимо сначала прологарифмировать формулу измерения, а затем продифференцировать её по всем аргументам:
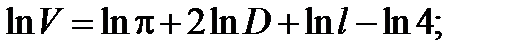
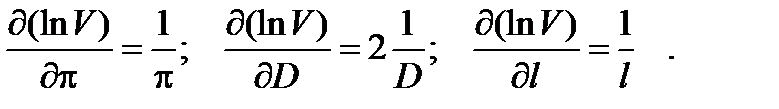
Расчётная формула погрешности имеет вид
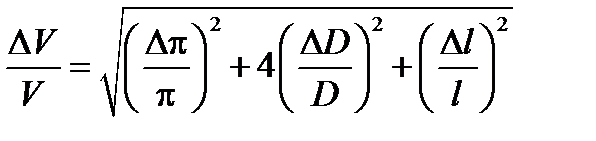 .
.
Значение p при расчёте надо взять с такой точностью, чтобы (Dp/p)2 было существенно меньше остальных слагаемых в этой формуле и им можно было пренебречь. Таким образом, если это сделано:
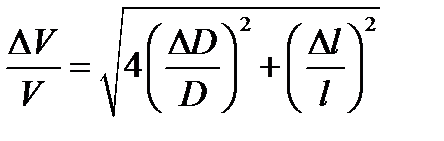 .
.
Пусть измерение длины – прямое измерение стальной рулеткой с миллиметровыми делениями. Приборную погрешность оценим в половину цены деления:
D l приб = 0,5 мм.
Измерение длины, проведённое тщательно с многократной проверкой, дало 552 мм, причём разброс не обнаружен, т.е. случайной ошибки нет. Запишем результат измерения длины
l = (552 ± 0.5) мм.
Измерение диаметра – прямое измерение микрометром с приборной погрешностью D Dприб = 0,005 мм. Многократные измерения диаметра, проведённые тщательно в различных местах под различными направлениями, дали следующие результаты: 2,58 мм; 2,57 мм; 2,60 мм; 2,54 мм; 2,55 мм; 2,58 мм. Наблюдаемый разброс результатов измерений свидетельствует о наличии случайной ошибки, возникновение которой вероятнее всего связано с отличием формы проволоки от идеальной. Обработаем полученные результаты, заполняя табл.2.
Порядок действий
1. Первая графа – указать номер отдельного измерения по порядку.
2. Во вторую графу занести полученные результаты измерений. Наименование единицы измерения и общий множитель, характеризующий порядок величины, дают в заголовке графы вместе с символом измеряемой величины.
3. Определить среднее арифметическое по всем данным второй графы. Полученное значение записать под второй графой.
Таблица 2
Обработка результатов измерения диаметра
| Номер измерения | Di /мм | D Di ×102 /мм | D Di2 ×104 /мм2 |
| 2,58 | |||
| 2,57 | |||
| 2,60 | |||
| 2,54 | -3 | ||
| 2,55 | -2 | ||
| 2,58 | |||
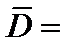 2,57 мм 2,57 мм
| S= 24×10-4 мм2 |
4. Третья графа – отклонения результата каждого измерения от среднего значения. Можно провести проверку вычисления среднего, используя равенство 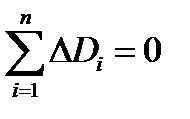 .
.
5. Четвёртая графа – 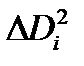 .
.
6. Подсчитать сумму четвёртой графы, результат записать под ней.
7. Выбрать доверительную вероятностьa (взять значение, указанное преподавателем). Например, a = 0,9.
8. По таблице коэффициентов Стьюдента (см. табл. 1) найти значение t 0,9,n = 2,0.
9. Рассчитать случайную погрешность

10. Рассчитать полную погрешность
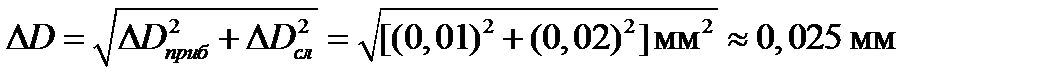
11. Записать результат измерения диаметра
D = (2,57 ± 0,025) мм (a = 0,9).
Таким образом производится обработка прямых измерений при наличии случайной ошибки.
После того как произведены и обработаны результаты прямых измерений, можно проводить расчёт объёма и его погрешности. Лучше начать с расчёта погрешности
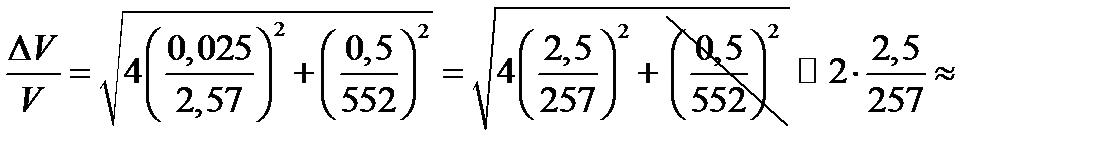
0,02 = 2 %
Расчёт объёма достаточно вести до трёх значащих цифр
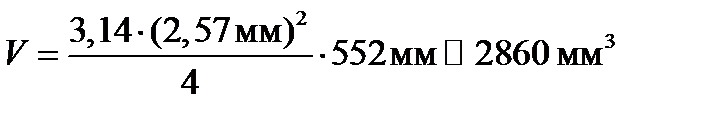 .
.
Погрешность D V составляет 2 % от V: D V » 60 мм3.
Запишем окончательный результат
V = (2860 ± 60) мм3 = (2,86 ± 0,06)×10–6 м3 (a = 0,9).
Задания для студентов
Задание №1. Результаты измерения диаметра свинцового шарика микрометром с приборной погрешностью 0.01 мм: 5.06, 5.02, 5.06, 5.01, 5.07, 5.03, мм. Полагая плотность свинца равной 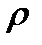 = (1.34 ± 0.05) г/см3, определить массу шарика и рассчитать погрешность для
= (1.34 ± 0.05) г/см3, определить массу шарика и рассчитать погрешность для 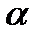 = 0.8.
= 0.8.
Задание №2. Результаты измерения диаметра шара микрометром с ценой деления 0.01 мм: 15.06, 15.02, 15.06, 15.01, 15.07, 15.03, мм. Определить площадь поверхности шара и рассчитать погрешность для  = 0,9.
= 0,9.
Задание №3. Определить сопротивление лампочки. Результаты измерения силы тока амперметром (класс точности 1.0, предел измерения 10А) 2.2А.Результаты измерения напряжения вольтметром (класс точности 0.5, предел измерения 500 В): 215.6, 215.2, 215.6, 215.1, 215.7, 215.3, В. Рассчитать погрешность для 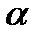 = 0.8.
= 0.8.
Задание №4. Рассчитать мощность электронагревателя. Результаты измерения напряжения вольтметром (класс точности 2.0, предел измерения 250В) 220В. Результаты измерения силы тока цифровым амперметром. 2,06, 2.02, 2.06, 2.01, 2.07,2.03, А. Рассчитать погрешность для 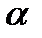 =0.9.
=0.9.
Задание №5. Результаты измерения внутреннего и внешнего диаметров кольца рулеткой с миллиметровыми делениями: 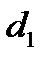 :131.5, 134, 133, 132.5, 134, 135, мм.;
:131.5, 134, 133, 132.5, 134, 135, мм.; 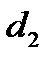 : 258, 256, 255.5, 254, 256.5, 257, мм. Определить площадь кольца и рассчитать погрешность для
: 258, 256, 255.5, 254, 256.5, 257, мм. Определить площадь кольца и рассчитать погрешность для 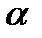 = 0.8.
= 0.8.
Задание №6. Определить длину границы круглого участка. Результаты измерения диаметра круглого участка рулеткой с миллиметровыми делениями: 10506, 10502,10506, 10510,10501, 10507, 10503, мм. Определить.длину границы круглого участка и рассчитать погрешность для 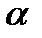 = 0.9.
= 0.9.
Задание №7. Определить циклическую частоту электромагнитных колебаний 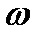 , создаваемых генератором, если результаты намерения периода Т цифровым миллисекундомером таковы: 1.0061, 1.0022, 1.0065, 1.0008, 1 0071, 1 0034, мс. Рассчитать погрешность для
, создаваемых генератором, если результаты намерения периода Т цифровым миллисекундомером таковы: 1.0061, 1.0022, 1.0065, 1.0008, 1 0071, 1 0034, мс. Рассчитать погрешность для 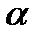 = 0.8.
= 0.8.
Задание №8. Определить частоту электромагнитных колебаний в колебательном контуре, если его катушка имеет индуктивность (25.4 ± 0.5)мГн, а результаты измерения емкости конденсатора цифровым измерительным местом в пикофарадах следующие: 4061, 4022, 4065, 4008, 4071, 4034, 4010. Рассчитать погрешность для 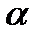 = 0.8.
= 0.8.
Задание №9. Рассчитать период колебаний маятника, длина которого 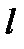 была измерена штангенциркулем с ценой деления 0.1 мм.Результаты измерений
была измерена штангенциркулем с ценой деления 0.1 мм.Результаты измерений 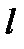 : 215.6, 215.2, 215.6, 215.0, 215.7, 215.3, мм. Стандартное значение ускорения свободного падения
: 215.6, 215.2, 215.6, 215.0, 215.7, 215.3, мм. Стандартное значение ускорения свободного падения 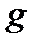 = (980.6 ± 0.6) см/с2. Рассчитать погрешность для
= (980.6 ± 0.6) см/с2. Рассчитать погрешность для 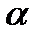 = 0.7.
= 0.7.
Задание № 10. Рассчитать кинетическую энергию пули на вылете из ствола, если ее масса 9.983 ± 0.006 г. Результат измерения скорости методом скоростной киносъемки 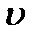 , м/с: 1502, 1501,1506, 1503,1506, 1507, 1503 Приборная погрешность метода
, м/с: 1502, 1501,1506, 1503,1506, 1507, 1503 Приборная погрешность метода 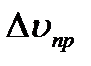 = 1.5м/с. Рассчитать погрешность для
= 1.5м/с. Рассчитать погрешность для 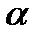 = 0 7
= 0 7
Задание №11. Определить максимальную высоту подъема пули при выстреле из вертикального ствола, если результаты измерения скорости пули на вылете из ствола методом скоростной киносъемки в м/с: 806, 802, 806, 801, 807, 803. Приборная погрешность метода 1.5 м/с. Стандартное значение ускорения свободного падения 980.665 см/с2. Рассчитать погрешность для 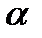 =0.7.
=0.7.
Задание №12. Определить атмосферное давление в килопаскалях, если показания ртутного барометра дали следующие результаты в мм рт. столба: 765.65, 765.20, 765.60, 765.05, 765.70, 765.30. Плотность ртути 13.6 ± 0.5 г/см3. Стандартное значение ускорения свободного падения 980.665 см/с2. Рассчитать погрешность для 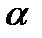 = 0.8.
= 0.8.
Задание №13. Определить заряд на конденсаторе емкостью 10 мкф (относительная погрешность 2.5%). Результаты измерения напряжения вольтметром (класс точности 1.0 на пределе 500 В): 216, 215, 211, 217, 213, 212 В. Рассчитать погрешность для 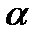 = 0.7.
= 0.7.
Задание №14. Энергия фотона определяется по результатам измерения длины волны 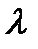 с помощью интерферометра. Результаты измерения
с помощью интерферометра. Результаты измерения 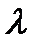 в ангстремах: 4061, 4022, 4065, 4008, 4071, 4034 с приборной погрешностью 10 А°. Постоянная Планка 6.б26•10-34 Дж*с. Скорость света в вакууме 2.998*108 м/с. Определить энергию фотона и рассчитать погрешность для
в ангстремах: 4061, 4022, 4065, 4008, 4071, 4034 с приборной погрешностью 10 А°. Постоянная Планка 6.б26•10-34 Дж*с. Скорость света в вакууме 2.998*108 м/с. Определить энергию фотона и рассчитать погрешность для 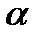 = 0.8.
= 0.8.
Задание №15. Для определения объема цилиндрической трубы измеряют ее длину 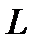 с помощью рулетки с ценой деления 1 мм и диаметры внутренний
с помощью рулетки с ценой деления 1 мм и диаметры внутренний 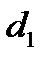 и наружный
и наружный 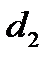 с помощью штангенциркуля с ценой деления 0.1 мм. В результате 6 измерений получены следующие значения:
с помощью штангенциркуля с ценой деления 0.1 мм. В результате 6 измерений получены следующие значения: 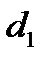 , мм: 22.3; 22.0; 21.8; 22.2; 22.1; 21.7.
, мм: 22.3; 22.0; 21.8; 22.2; 22.1; 21.7. 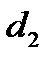 , мм: 27.6; 27.1; 27.9; 27.3; 27.0; 27.6.
, мм: 27.6; 27.1; 27.9; 27.3; 27.0; 27.6. 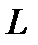 , мм: 582,0 Определить объем трубы и рассчитать погрешность для
, мм: 582,0 Определить объем трубы и рассчитать погрешность для 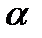 = 0.8.
= 0.8.
Задание №16. Показатель преломления среды определяется по результатам измерения угла полного внутреннего отражения (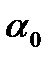 ):
): 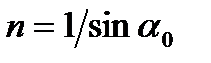 . В результате прямых измерений угла
. В результате прямых измерений угла 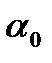 (в градусах): 41.8, 41.0, 41.6, 42.2, 41.2 с приборной погрешностью 6 минут. Определить показатель преломления и рассчитать погрешность для
(в градусах): 41.8, 41.0, 41.6, 42.2, 41.2 с приборной погрешностью 6 минут. Определить показатель преломления и рассчитать погрешность для 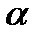 = 0.95.
= 0.95.
Задание №17. Коэффициент трения тела на наклонной плоскости определяется по критическому углу (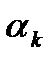 ), при котором тело начинает скользить:
), при котором тело начинает скользить: 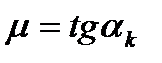 . Результаты прямых измерений угла
. Результаты прямых измерений угла 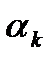 в градусах: 61.5; 60.8; 62.0; 61.2; 60.5 с приборной погрешностью 1°. Определить
в градусах: 61.5; 60.8; 62.0; 61.2; 60.5 с приборной погрешностью 1°. Определить 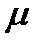 и рассчитать погрешность для а
и рассчитать погрешность для а 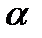 = 0.9.
= 0.9.
Задание №18. Ускорение свободного падения 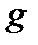 определяют по результатам прямых измерений периода Т и длины
определяют по результатам прямых измерений периода Т и длины 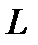 математического маятника. Т, с: 1.09; 1.11; 1.17; 1.13; 1.10; 1.15 с приборной погрешностью секундомера 0.02 с.
математического маятника. Т, с: 1.09; 1.11; 1.17; 1.13; 1.10; 1.15 с приборной погрешностью секундомера 0.02 с. 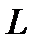 = (30.1± 0.05) см. Определить
= (30.1± 0.05) см. Определить 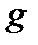 и рассчитать погрешность для
и рассчитать погрешность для 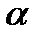 = 0.8.
= 0.8.
Задание № 19. Период колебаний физического маятника определяется по формуле: 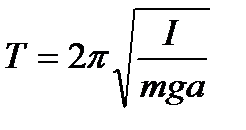 , где
, где  - момент инерция тела массой
- момент инерция тела массой 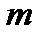 ,
, 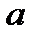 - расстояние от точки подвеса до центра масс. Определить момент инерции тела
- расстояние от точки подвеса до центра масс. Определить момент инерции тела 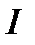 тела по результатам прямых измерений периода колебаний
тела по результатам прямых измерений периода колебаний 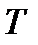 , с: 1.25; 1.38; 1.17; 1.20; 1.32; 1,41.
, с: 1.25; 1.38; 1.17; 1.20; 1.32; 1,41.  = (20.1 ± 0.05), см;
= (20.1 ± 0.05), см; 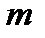 = (55.08 ±0.04) г. Стандартное значение ускорения свободного падения
= (55.08 ±0.04) г. Стандартное значение ускорения свободного падения 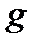 = 980.665 см/с2. Рассчитать погрешность для
= 980.665 см/с2. Рассчитать погрешность для 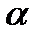 = 0.8.
= 0.8.
Задание №20. Добротность колебательной системы 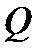 определяется по результатам прямых измерений частот колебаний
определяется по результатам прямых измерений частот колебаний 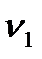 и
и 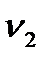 , при которых амплитуда колебаний уменьшается в
, при которых амплитуда колебаний уменьшается в 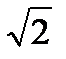 раза по сравнению с амплитудой колебаний при резонансной частоте
раза по сравнению с амплитудой колебаний при резонансной частоте 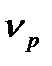 :
: 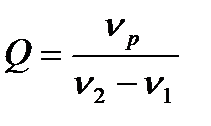 ,
, 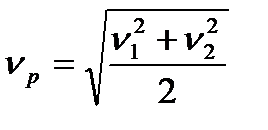 . Измерения частот с приборной погрешностью
. Измерения частот с приборной погрешностью 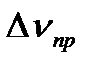 = ± 2Гц дали следующие результаты:
= ± 2Гц дали следующие результаты: 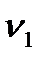 *103, Гц: 3.752; 3761; 3.758; 3.756; 3.760; 3.764.
*103, Гц: 3.752; 3761; 3.758; 3.756; 3.760; 3.764. 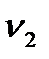 *103, Гц: 3.846; 3852; 3.855; 3.849; 3.850; 3.846. Определить
*103, Гц: 3.846; 3852; 3.855; 3.849; 3.850; 3.846. Определить 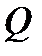 и рассчитать погрешность для
и рассчитать погрешность для 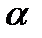 = 0.9.
= 0.9.
Задание № 21. Момент инерции алюминиевого стержня квадратного сечения определяется по формуле: 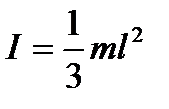 , где масса
, где масса 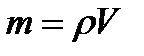 , объем
, объем 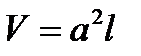 Длина стержня
Длина стержня 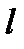 измеряется с помощью мм-линейки:
измеряется с помощью мм-линейки: 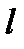 =38,7 см. Измерения размера а с помощью штангенциркуля (цена деления 0.1мм): 2.68, 2.51, 2.59, 2.49, 2.50, 2.54, см. Полагая плотность алюминия
=38,7 см. Измерения размера а с помощью штангенциркуля (цена деления 0.1мм): 2.68, 2.51, 2.59, 2.49, 2.50, 2.54, см. Полагая плотность алюминия 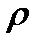 = (2.72 ± 0.07) г/см3, определить величину
= (2.72 ± 0.07) г/см3, определить величину 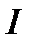 и рассчитать погрешность для
и рассчитать погрешность для 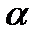 = 0.95.
= 0.95.
Задание № 22. Момент инерции алюминиевого диска толщиной h и диаметром D определяется по формуле: 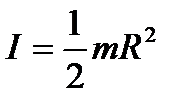 , где масса
, где масса 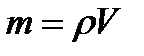 , объем
, объем 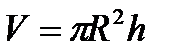 . Результаты измерений
. Результаты измерений  и
и 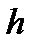 с помощью штангенциркуля (цена деления 0.1 мм):
с помощью штангенциркуля (цена деления 0.1 мм):  , см - 54.73; 54.58; 54.65; 54.59; 54.61; 54,69.
, см - 54.73; 54.58; 54.65; 54.59; 54.61; 54,69. 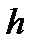 , см - 2.68, 2.51,2.59, 2.49, 2.50, 2.54. Полагая плотность алюминия
, см - 2.68, 2.51,2.59, 2.49, 2.50, 2.54. Полагая плотность алюминия 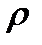 = (2.72 ± 0.07) г/см3, определить величину
= (2.72 ± 0.07) г/см3, определить величину 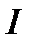 и рассчитать погрешность для
и рассчитать погрешность для  = 0.8.
= 0.8.
Задание № 23. Момент инерции стального шара диаметром  определяется по формуле:
определяется по формуле:  , где масса
, где масса 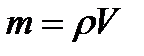 , объем
, объем 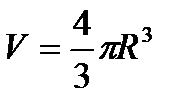 . Результаты измерений
. Результаты измерений  с помощью штангенциркуля (цена деления 0.1мм): 22.3; 22.0; 21.8; 22.2; 22.1; 21,7, см. Полагая плотность стали
с помощью штангенциркуля (цена деления 0.1мм): 22.3; 22.0; 21.8; 22.2; 22.1; 21,7, см. Полагая плотность стали 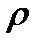 = (7.66± 0.05) г/см3, определить величину I и рассчитать погрешность для
= (7.66± 0.05) г/см3, определить величину I и рассчитать погрешность для 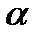 = 0.75.
= 0.75.
Задание № 24. Момент инерции медного цилиндра длиной 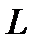 и диаметром
и диаметром  определяется по формуле:
определяется по формуле: 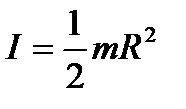 , где масса
, где масса 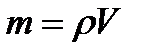 , объем
, объем 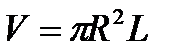 . Результата прямых измерений с помощью штангенциркуля (цена деления 0.1 мм) длины
. Результата прямых измерений с помощью штангенциркуля (цена деления 0.1 мм) длины 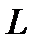 = 102,4 мм и диаметра
= 102,4 мм и диаметра  : 57.3, 58.1, 57.0, 56.8, 56.6, 57.8, мм. Полагая плотность стали
: 57.3, 58.1, 57.0, 56.8, 56.6, 57.8, мм. Полагая плотность стали 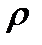 = (8,89 ± 0.05) г/см3, определить величину
= (8,89 ± 0.05) г/см3, определить величину  и
и 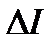 для
для 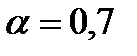 .
.
Задание № 25. Масса тонкой титановой сферы, полученная взвешиванием с приборной погрешностью 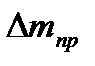 = 0.5г, равна 296.6 г. Результаты прямых измерений с помощью штангенциркуля (цена деления 0.1мм) диаметра сферы
= 0.5г, равна 296.6 г. Результаты прямых измерений с помощью штангенциркуля (цена деления 0.1мм) диаметра сферы  :19.8, 20.7,21.0, 19.5, 20.4, 21.6. Полагая плотность титана
:19.8, 20.7,21.0, 19.5, 20.4, 21.6. Полагая плотность титана 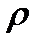 = (4,55 ± 0.05) г/см3, определить толщину сферы и рассчитать погрешность для
= (4,55 ± 0.05) г/см3, определить толщину сферы и рассчитать погрешность для  = 0.7.
= 0.7.
Задание № 26. Плотность льда определяется по результатам прямых измерений высоты 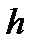 надводной части ледяного куба с длиной ребра
надводной части ледяного куба с длиной ребра  , плавающего в воде:
, плавающего в воде: 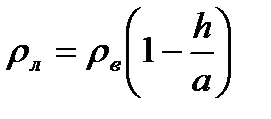 , где плотность воды
, где плотность воды 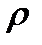 = (1.02±0.01) г/см3. В результате измерений с помощью мм-линейки получены следующие данные:
= (1.02±0.01) г/см3. В результате измерений с помощью мм-линейки получены следующие данные:  , мм: 56, 58, 54, 55.5, 57, 56.5;
, мм: 56, 58, 54, 55.5, 57, 56.5; 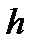 , мм: 5.5, 6.5, 4.0, 6.0, 7.0, 5.0. Определить плотность льда и рассчитать погрешность для
, мм: 5.5, 6.5, 4.0, 6.0, 7.0, 5.0. Определить плотность льда и рассчитать погрешность для 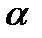 = 0.8.
= 0.8.