Делим исходный временной ряд на две примерно равные по числу уровней части:
n1=7, n2=8 (n1+ n2=n=15).
Для каждой из этих частей вычисляем средние значения и дисперсии:
74,476
16,696
Проверяем гипотезу о равенстве (однородности) дисперсий обеих частей ряда с помощью F -критерия Фишера. Для вычисления F -критерия большую дисперсию делим на меньшую:
Так как 
, то с вероятностью 95% есть основание отвергать нулевую гипотезу, выборочные дисперсии (
и 
) различаются значимо (расхождение между ними неслучайно).
Проверяем основную гипотезу о равенстве средних значений с использованием t -критерия Стьюдента:
Подставляя числовые значения, получим
=5,07
t табл(0,05;13)=2,16
Так как 
, то есть основание отвергать нулевую гипотезу о равенстве средних, расхождение между вычисленными средними значимо. Отсюда вывод: имеется тенденция в данном временном ряду.
Рассмотрим решение данного примера в Excel.
Гипотезу о равенстве дисперсий проверим с помощью F -теста, который можно найти среди инструментов Анализа данных (рис. 2).
Рисунок 2
 |
. Вызов надстройки Excel Анализ данных
Вводим данные для выполнения F -теста, указывая интервал для первой и второй переменных (рис. 3).
Рисунок 3
 |
. Ввод данных для выполнения F -теста
Результат выполнения теста приведен в табл. 3.
Таблица 3. Результат выполнения F -теста
| Двухвыборочный F-тест для дисперсии | ||
| Переменная 1 | Переменная 2 | |
| Среднее | 80,85714286 | 98,125 |
| Дисперсия | 74,47619048 | 16,69642857 |
| Наблюдения | ||
| df | ||
| F | 4,460606061 | |
| P(F<=f) одностороннее | 0,035392599 | |
| F критическое одностороннее | 3,865968853 |
Анализируя результаты выполнения двухвыборочного F -теста для проверки гипотезы о равенстве дисперсий, приходим к выводу, что исправленные выборочные дисперсии ( и ) различаются значимо. Таким образом, убеждаемся, что имеется тенденция.
Используя средства Excel, построить следующие виды трендовых моделей: линейную, логарифмическую, полиномиальную, степенную, экспоненциальную, линейной фильтрации.
Построим линейную трендовую модель для данного временного ряда.
Линейная форма тренда: 
.
Уравнение линейного тренда имеет вид: 
Рисунок 4. Линейный тренд для временного ряда
Построим логарифмическую трендовую модель для данного временного ряда, используя средства Excel.
Логарифмическая форма тренда: 
.
Для данного временного ряда 
= 68,90 + 11,37ln t.
Рисунок 5. Логарифмический тренд для временного ряда
Построим полиномиальную трендовую модель для данного временного ряда, используя средства Excel.
Полиномиальнаяформа тренда имеет вид: 
.
Для данного временного ряда = 67,98 + 4,021t - 0,122t2.
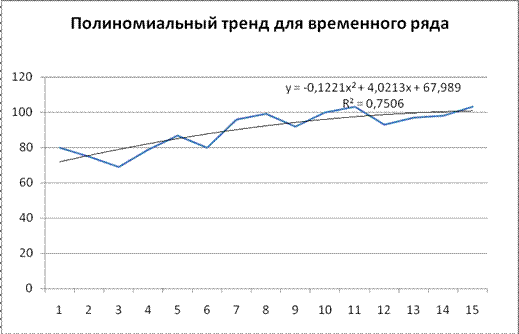
Рисунок 6. Полиномиальный тренд временного ряда
Построим степенную трендовую модель для данного временного ряда, используя средства Excel.
Степеннаяформа тренда имеет вид: 
.
Для данного временного ряда = 70,1t0,13.
Рисунок 7. Степенной тренд для временного ряда
Построим экспоненциальную трендовую модель для данного временного ряда, используя средства Excel.
Экспоненциальнаяформа тренда имеет вид: 
.
Для данного временного ряда = 73,96e0,023t.
Рисунок 8. Экспоненциальный тренд для временного ряда
Построим линейную фильтрацию для данного временного ряда, используя средства Excel.
Рисунок 9. Линейная фильтрация для временного ряда
Сравнить качество построенных моделей, используя коэффициент детерминации и среднюю относительную ошибку (СОО). Данные представить в таблице. Выбрать лучшую модель. Выводы обосновать.
Таблица 4. Сравнение качества построенных моделей
| Модель тренда | Уравнение | R2 | СОО |
| Линейная | y = 2,067t + 73,52 | 0,714 | 5,62 |
| Логарифмическая | y = 11,37ln(t) + 68,9 | 0,660 | 13,46 |
| Полиномиальная | y = -0,122t2+4,021t+67,98 | 0,750 | 5,28 |
| Экспоненциальная | y = 73,96e0,023t | 0,702 | 5,7 |
| Степенная | y = 70,10t0,13 | 0,652 | 5,69 |
Анализируя полученные значения коэффициента детерминации (R2), приходим к выводу, что лучшей моделью для временного ряда является полиномиальная, так как у нее наивысший коэффициент детерминации.
Полученные значения средней относительной ошибки (СОО), представленные в таблице, также говорят о достаточно высоком уровне точности полиномиальной модели (ошибка менее 5% свидетельствует об удовлетворительном уровне точности; ошибка в 10 и более процентов считается очень большой).