Дана произвольная форма А = А (А1,…Аn).
Высказывание, полученное из формы А подстановкой вместо букв конкретных простых высказываний называется частным случаем формы. У одной формы может быть бесконечное число частных случаев формы.
Форма А называется выполнимой, если существует набор значений букв не которых А равно истине (А =И) (у формы существует истинный частный случай).
Форма А называется тавтологией, если она истинна при любых значениях букв, то есть порождает тождественно истинную функцию (а таблице одни истины).
Форма А называется противоречием, если ложна при всех значениях букв, то есть порождает тождественно ложную функцию (в таблице одна ложь).
Высказывание называется логически истинным, если оно является частным случаем тавтологии или логическим ложным, если оно является частным случаем противоречия.
Истинное высказывание.
Логически истинное высказывание истинно в силу своей структуры, а не содержания.
А =АvА – тавтология
Пример:
А =(2×2=5) или (2×2≠5) = И – логически истинное высказывание
То же самое относится и к логически ложным высказываниям.
А ~Т – означает, что форма является тавтологией.
А ~П означает, что форма является противоречием.
Проблема выполнимости логики высказываний.
Пусть дана произвольная форма А = А (А1,…Аn).
Проблема: существует ли метод, позволяющий за конечное число шагов или действий выяснить выполнимость произвольно заданной формы?
А может быть выполнимой, не выполнимой (А ~П), тавтологией (А ~Т, частный случай выполнимой формы).
А ~П ↔ А ~Т – форма А является противоречием тогда и только тогда, когда А является тавтологией.
Такой метод существует и он называется методом построения таблиц.
Количество строк определяется формулой 2n, где n кол-во переменных.
Если форма содержит К связок, то нужно выполнить К операций.
Чтобы вычислить форму необходимо К×2n < ∞ (число конечное).
Этот метод не совсем удобен.
Существует другой метод, основанный на построении других форм Д.Н.Ф. и К.Н.Ф.
Равносильность форм.
Пусть даны две А,В формы. Они называются равносильными, если имеют одинаковые значения при любых значениях букв, входящих в них, то есть имеют одинаковые таблицы истинности (порождают одну и ту же истинностную функцию).
Записывается А ~ В (форма А равносильна В форме).
Отношение равносильности ~ рефлексивно (А ~ А), симметрично (А ~ В, то В,~ А), транзитивно (А ~ В и В ~С, то А~С).
Отношение равносильности разбивает множество формул на классы. Все формулы одного класса равносильны, порождают одну и ту же функцию (одна и та же таблица).
Признаком класса является таблица. Формулы разных классов не равносильны. Равносильность высказываний означает одинаковость смыслов тех высказываний, которые являются частными случаями форм.
Теорема о подстановке.
Если в некоторой форме А заменить подформу на равносильную ей формулу, то получится форма В равносильная А.
Основные законы логики высказываний:
Каждый закон представляется как равносильность двух форм.
1. Закон двойного отрицания: 
2. Закон коммутативности: 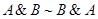 ,
, 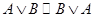
3. Ассоциативности (сочетательные):
4. 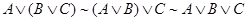

5. Дистрибутивность (распределительные):
 – дистрибутивность конъюнкции,
– дистрибутивность конъюнкции,
 – дистрибутивность дизъюнкции.
– дистрибутивность дизъюнкции.
Эти операции взаимно дистрибутивны.
6. Законы де Моргана: 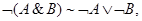
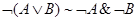 .
.
7. Законы идемпотентности:  ,
,  .
.
8. Закон исключенного третьего:  (
(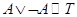 ).
).
9. Закон противоречия: 
10. Законы поглощения:  ,
, 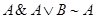 ,
, 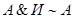 ,
, 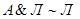 ,
, 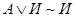 ,
, 
(в последних четырех формулах И можно заменить на Т, а Л – на П).
В 9 законе присутствуют только 3 операции -,&,v – они главные. Не главные операции выражаются через главные.
10. Закон исключения импликации: 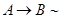
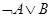 .
.
11. Закон исключения эквивалентности: 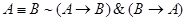 .
.
Все законы являются справедливыми, если в них буквы заменить произвольными формами.
Лекция 4.
Нормальные формы.
Теорема 1.
Для любой формы существуют равносильные ей ДНФ и КНФ (дизъюнктивная нормальная форма и конъюнктивная нормальная форма).
Пусть дана форма А = А (А1,…Аn). Переход к ДНФ.
1) Исключаем все связки, кроме,&,v (законы 10, 11).
2) Вносим отрицания в скобки, то есть добиваемся «тесных» отрицаний (закон 5).
3) Раскрываем все скобки по законы дистрибутивности конъюнкций (закон 4).
4) Получаем ДНФ.
ДНФ состоит из дизъюнкций элементарных конъюнкций.
Переход к КНФ.
1) Исключаем все связки, кроме,&,v (законы 10, 11).
2) Вносим отрицания в скобки, то есть добиваемся «тесных» отрицаний (закон 5).
3) Раскрываем скобки по закону дистрибутивности дизъюнкции (закон 4).
4) Получаем КНФ.
КНФ состоит из конъюнкции элементарных дизъюнкций.
Проблему выполнимости можно решить с помощью ДНФ и КНФ.
Теорема 1.
Форма выполнима, то есть не является противоречием тогда и только тогда, когда равносильная ей ДНФ содержит хотя бы одно слагаемое, в котором нет пары множителей А&А.
Теорема 2.
Форма не выполнима, то есть является противоречием тогда и только тогда, когда равносильная ей ДНФ в каждом слагаемом содержит пару множителей А&А.
А не выполнима (~П)↔ А&А.
Форма А является тавтологией тогда и только тогда, когда равносильная ей КНФ содержит в каждом множителе пару слагаемых вида АvА.
Пример:
А = 
 ~
~  – ДНФ, формула выполнима.
– ДНФ, формула выполнима.
Из этой формулы можно получить истинные частные случаи, модель для истинных высказываний.
Для того, чтобы выяснить, при каких значениях выполняется форма нужно принять буквы с отрицанием как ложь, без отрицания – истину.
Из данного примера можно получить 5 вариантов истинны высказывания (А=Л, В=И, С=Л; В=Л). С помощью КНФ распознаем тавтологию. Так как нет пары, это не тавтология. Из этой формы можно получить и истину, и ложь. Ложные при А=И, В=И; В=И, С=И.