1.Построить графики функций распределения и плотностей распределения следующих распределений:
А) Фишера (при степенях свободы df1 =10 и df2 =10; df1 =2 и df2 =50; df1 =10 и df2 =50; df1 =10 и df2 =500, df1 =30 и df2 =1000);
Б) Стьюдента (при степенях свободы df =10; df =50; df =200);
В) показательного (при параметре λ=0,5; λ=5; λ=20);
Г) χ2-распределения (при степенях свободы df =10; df =50; df =200);
Д) логнормального (при μ =0, σ= 1; μ= 1, σ= 2);
Е) нормального (при μ =0, σ= 1; μ= 1, σ= 2).
2. Проанализировать изменение графиков функций и плотности рассмотренных распределений при изменении параметров распределений (степеней свободы).
4.Определить критическое значение статистик по заданному р -уровню (р =0,99, р =0,95, р =0,9) и степеням свободы (параметрам распределения) для следующих распределений:
А) Фишера (при степенях свободы df1 =10 и df2 =10; df1 =2 и df2 =50; df1 =10 и df2 =50; df1 =10 и df2 =500, df1 =30 и df2 =1000);
Б) Стьюдента (при степенях свободы df =10; df =50; df =200);
В) показательного (при параметре λ=0,5; λ=5; λ=20);
Г) χ2-распределения (при степенях свободы df =10; df =50; df =200);
Д) логнормального (при μ =0, σ= 1; μ= 1, σ= 2);
Е) нормального (при μ =0, σ= 1; μ= 1, σ= 2).
5.Определить уровень доверия р по заданному значению критической статистики и соответствующим степеням свободы:
А) Фишера (при степенях свободы df1 =10 и df2 =10 и значении F =1,55; df1 =2 и df2 =50 и значении F =2,33; df1 =10 и df2 =50 и значении F =4,8; df1 =10 и df2 =500 и значении F =1,72, df1 =30 и df2 =1000 и значении F =1,35);
Б) Стьюдента при односторонней проверке (при степенях свободы df =10 и значении t =1,37; df =50 и значении t =2,11; df =200 и значения t =0,55);
В) Стьюдента при двусторонней проверке (при степенях свободы df =10 и значении t =1,37; df =50 и значении t =2,11; df =200 и значения t =0,55);
Г) показательного (при параметре λ=0,5 и значении exp=1,38; λ=5 и значении exp=0,6; λ=20 и значении exp=0,23);
Д) χ2-распределения (при степенях свободы df =10 и значении χ2=12,54; df =50 и значении χ2=67,54; df =200 и значении χ2=220);
Е) логнормального (при μ =0, σ= 1 и значении L =1,96; μ= 1, σ= 2 и значении L =72,96);
Ж) нормального (при μ =0, σ= 1 и значении Z=1,96; μ= 1, σ= 2 и значении Z=2,67).
№1. Построить графики функций распределения и плотностей распределения следующих распределений:
А) Функции распределения Фишера

График 1. Df1=10 df2=10

График 2. Df1=2 df2=50

График 3. Df1=10 df2=50

График 4. Df1=10 df2=500

График 5. Df1=30 df2=1000
Б) Функции распределения Стьюдента
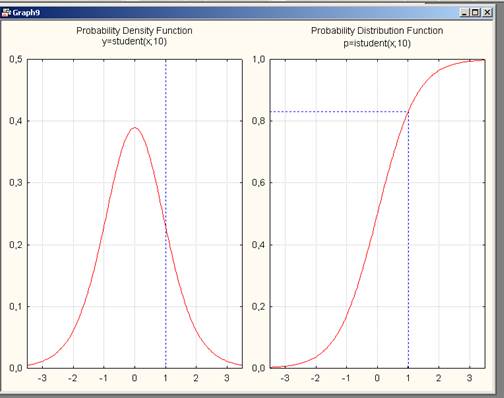
График 6. Df=10

График 7. Df=50

График 8. Df=200
В) Функции показательного распределения

График 8. λ=0,5

График 9. λ=5

График 9. λ=200
Г) Функции χ2 - распределения

График 10. df=10

График 11. df=50

График 12. df=200
Е) Функции логнормального распределения

График 13. μ=0 σ=1

График 14. μ=1 σ=2
Д) Функции логнормального распределения

График 13. μ=0 σ=1

График 14. μ=1 σ=2
№2. Проанализировать изменение графиков функций и плотности рассмотренных распределений при изменении параметров распределений (степеней свободы).
Мы проанализировали изменение графиков функции и плотности рассмотренных распределений при изменении параметров распределений.
В графике Фишера при степенях свободы df1 =10 и df2 =10 плотность распределения смещается влево и вверх, а функция распределения вверх. А при степенях свободы df1 =2 и df2 =50 плотность распределения смещается влево и вниз, а функция распределения вверх. В дальнейшем степень свободы увеличивается и плотность распределения снова смещается влево и вверх, а функция распределения вверх. При увеличении степени свободы график функции распределения стремится к нормальному.
В графике Стьюдента при увеличении степени свободы плотность распределения смещается вверх и функция распределения вверх.
В показательном графике при увеличении параметров плотность распределения смещается влево и вверх а функция распределения вверх.
В графике хи-квадрат распределения при увеличении степени свободы плотность распределения смещается вниз и функция распределения вниз.
В логнормальном графике при увеличении параметров плотность распределения смещается вниз и функция распределения вниз
В нормальном графике при увеличении параметров плотность распределения смещается вправо и функция распределения вправо.
№4 Определить критические значение статистик по заданному p-уровню (p=0,99, p=0,95, p=0,9) и степеней свободы (параметрам распределения) для следующих распределений:
А) Фишер
P=0.99
10/10 F=4,849147
2/50 F= 5,056611
10/50 F= 2,698139
10/500 F= 2,356455
30/1000 F= 1,715844
P=0.95
10/10 F= 2,978237
2/50 F= 3,182610
10/50 F= 2,026143
10/500 F= 1,849637
30/1000 F= 1,470594
P=0.9
10/10 F= 2,322604
2/50 F= 2,411955
10/50 F= 1,729150
10/500 F= 1,611513
30/1000 F= 1,350073
Б) Стьюдента
P=0.99
10 T=2,763769
50 T= 2,403272
200 T= 2,345137
P=0.95
10 T= 1,812461
50 T= 1,675905
200 T= 1,652508
P=0.9
10 T= 1,372184
50 T= 1,298714
200 T= 1,285799
В) Показательного
P=0.99
λ=0,5 E= 9,210340
λ=5 E=,921034
λ=20 E=,230259
P=0.95
λ=0,5 E= 5,991465
λ=5 E=,599146
λ=20 E=,149787
P=0.9
λ=0,5 E= 4,605170
λ=5 E=,460517
λ=20 E=,115129
Г) Х2 распределения
P=0.99
df=10 Chi= 23,209251
df=50 Chi= 76,153891
df=200 Chi= 249,445123
P=0.95
df=10 Chi= 18,307038
df=50 Chi= 67,504807
df=200 Chi= 233,994269
P=0.9
df=10 Chi= 15,987179
df=50 Chi= 63,167121
df=200 Chi= 226,021048
Д) логнормального
P=0.99
μ=0 σ=1 L= 10,240474
μ=1 σ=2 L= 285,058880
P=0.95
μ=0 σ=1 L= 5,180252
μ=1 σ=2 L= 72,945111
P=0.9
μ=0 σ=1 L= 3,602224
μ=1 σ=2 L= 35,272482
Е) нормального
P=0.99
μ=0 σ=1 X= 2,326348
μ=1 σ=2 X= 5,652696
P=0.95
μ=0 σ=1 X= 1,644854
μ=1 σ=2 X= 5,652696
P=0.9
μ=0 σ=1 X= 1,281552
μ=1 σ=2 X= 3,563103
№5. Определить критические значение статистик по заданному p-уровню (p=0,99, p=0,95, p=0,9) и степеней свободы (параметрам распределения) для следующих распределений:
А) Фишер
F=1.55
10/10 P=,749608
2/50 P=,777727
10/50 P=,850130
10/500 P=,881396
30/1000 P=,969491
F=2.33
10/10 P=,900823
2/50 P=,892227
10/50 P=,975779
10/500 P=,989084
30/1000 P=,999923
F=4.8
10/10 P=,989627
2/50 P=,987609
10/50 P=,999920
10/500 P=,999999
30/1000 P= 1,000000
F=1.72
10/10 P=,797138
2/50 P=,810509
10/50 P=,897881
10/500 P=,926635
30/1000 P=,990289
F=1.35
10/10 P=,677948
2/50 P=,731475
10/50 P=,768977
10/500 P=,799237
30/1000 P=,899960
Б) Стьюдента при односторонней
T=1.37
10 P=0,899671
T=2.11
50 P=0,980058
T=0.55
200 P=0,708533
В) Стьюдента при двусторонней
T=1.37
10 P=,799341
T=2.11
50 P=,960115
T=0.55
200 P=,417067
Г) Показательного
Е=1,38
λ=0.5 P=,498424
Е=0.6
λ=5 P=,950213
Е=0.23
λ=20 P=,989948
Д) Х2 распределения
Chi=12.54
df=10 P=,750000
Chi=67.54
df=50 P=,950297
Chi=220
df=200 P=,841721
E) Логнормального
L=1.96
μ=0 σ=1 P=0,749509
L=72.96
μ=1 σ=2 P=0,950011
Ж) нормального
Z=1.96
μ=0 σ=1 P=0,975002
Z=2.67
μ=1 σ=2 P=0,798141