Для удобства вместо одного дифференциального уравнения n -го порядка вводят в рассмотрение систему, состоящую из n дифференциальных уравнений первого порядка. Наряду с искомой функцией y вводят еще n – 1 вспомогательных искомых функций y 1, y 2,…, yn –1:
. (5.24)
Из этих соотношений следует, что
Поэтому 
, и тогда уравнение принимает вид
. (5.25)
Уравнения (5.24) и (5.25) представляют систему n дифференциальных уравнений с n искомыми функциями y 1, y 2,…, yn –1. Система такого вида, где в левых частях стоят производные от искомых функций, а правые части суть функции от независимой переменной и искомых функций, называется системой n дифференциальных уравнений первого порядка нормальной формы.
В целях обобщения вводят в рассмотрение вместо системы специального вида, представленной выше, систему n дифференциальных уравнений первого порядка общего вида относительно n искомых функций y 1, y 2,…, yn:
(5.26)
Для этой системы справедлива следующая теорема, которая приведена без доказательства.
Теорема 5.7 (теорема Коши). Пусть для системы дифференциальных уравнений первого порядка (5.26) выполняются следующие условия:
1) функции 
непрерывны по всем аргументам в замкнутой области D:
;
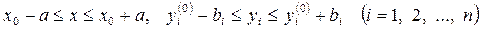2) частные производные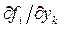 
непрерывны в области D. Тогда существует одна и только одна система решений уравнений (5.26):
,
определенная в некоторой окрестности точки x 0 и удовлетворяющая при x=x 0 заданным начальным условиям:
.
Теорема Коши утверждает существование частного решения системы обыкновенных дифференциальных уравнений (5.26), удовлетворяющего данным начальным условиям. Геометрически это означает, что существует одна интегральная кривая, проходящая через точку 
.
Введем вектор искомых функций 
и вектор правых частей уравнений (5.26) 
. Тогда векторная форма записи системы уравнений первого порядка имеет вид
.
Возвращаясь к случаю одного дифференциального уравнения n- го порядка, на основе этой теоремы Коши сформулируем соответствующую теорему существования и единственности решения.
Теорема 5.8. Уравнение 
правая часть которого непрерывна по всем аргументам и дифференцируема по ним в некоторой замкнутой области 
, имеет единственное решение, удовлетворяющее начальным условиям при 
:
, (5.30)
где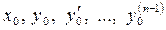 
- заданные числа.
Таким образом, теорема Коши определяет частное решение уравнения n- го порядка; общее решение этого уравнения содержит n произвольных постоянных:
.
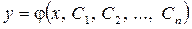Пример. Найти общее решение системы дифференциальных уравнений:
Решение. Дифференцируя одно из уравнений системы по t (например, первое уравнение) и исключая функцию y, сведем решение системы к решению уравнения второго порядка с постоянными коэффициентами. Решив это уравнение, найдем функцию x (t) а затем из первого уравнения найдем и функцию y (t).
Итак,
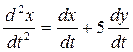. (I)
Из второго уравнения находим
и подставим в уравнение (I):
.
Наконец, найдем y из первого уравнения системы:
, (2)
.
После преобразований получаем однородное уравнение второго порядка с постоянными коэффициентами:
Решая характеристическое уравнение 
, получим 
,
.
Функцию y (t) находим, подставляя x (t) и 
в формулу (2):
.
Окончательно получим
.
Вопросы к экзамену
Производная и ее приложения
1. Определение производной, ее физический смысл. Необходимое условие дифференцируемости. Производные основных элементарных функций 
2. Производная суммы, произведения и частного двух дифференцируемых функций. Производные функций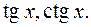 
3. Производная обратной функции. Производные функции 
4. Дифференцирование сложной функции, неявной функции, сложно – показательной функции и функции, заданной параметрически.
5. Дифференциал функции. Определение, вычисление, геометрический смысл, применение к приближенным вычислениям.
6. Теорема роля, теорема Лагранжа, теорема Коши. Правило Лопиталя.
7. Формула Тейлора с остаточным членом в форме Лагранжа. Формула Тейлора для основных элементарных функций 
8. Признаки монотонности функции.
9. Экстремумы функции. Необходимые и достаточные условия экстремумов (исследование функции на экстремум с помощью производных первого, второго, высших порядков).
10. Признаки выпуклости кривой. Точки перегиба кривой. Необходимые и достаточные условия наличия точек перегиба.
11. Производная от векторной функции скалярного аргумента, ее геометрический смысл.
Неопределенный интеграл
1. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой.
2. Интегрирование рациональных функций путем разложения на простейшие дроби. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных выражений. Использование таблиц интегралов.
Определенный интеграл
1. Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла.
2. Производная интеграла по верхнему пределу. Формула Ньютона – Лейбница.
3. Вычисление определенного интеграла: интегрирование по частям и подстановкой.
4. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов тел и площадей поверхностей вращения.
5. Кривизна плоскостей кривой. Кривизна пространственной кривой.
Дифференциальные уравнения
1. Дифференциальные уравнения первого порядка. Задача Коши. Теорема Коши. Понятие особого решения. Уравнения с разделяющимися переменными, однородные, линейные, уравнения Бернулли.
2. Дифференциальные уравнения высших порядков. Задача Коши. Теорема Коши. Уравнения, допускающие понижение порядка.
3. Линейные дифференциальные уравнения с постоянными коэффициентами. Общее решение, метод вариации. Уравнения с правой частью специального вида.
4. Нормальная система дифференциальных уравнений. Задача Коши. Теорема Коши. Метод исключения.