Тема:. Тригонометрические ряды Фурье
Тригонометрический ряд.
Разложение функций в степенные ряды, т.е. разложения сложных функций на простые степенные функции вида 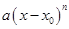 , не всегда возможны и не всегда удобны в приложениях.
, не всегда возможны и не всегда удобны в приложениях.
При изучении сложных периодических процессов естественно возникает задача о представлении функций, описывающих эти процессы в виде суммы конечного или бесконечного числа простых периодических функций.
В качестве таких функций берутся функции вида 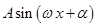 , или, что то же самое, функции вида
, или, что то же самое, функции вида 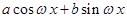 .
.
Если 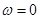 , то функция является постоянной, а если
, то функция является постоянной, а если 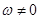 , то она является периодической с периодом
, то она является периодической с периодом 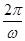 . В частности, каждая простая гармоника с
. В частности, каждая простая гармоника с 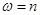 , где
, где 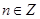 , имеет
, имеет 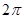 в качестве одного из своих периодов.
в качестве одного из своих периодов.
Рассмотрим задачу о разложении 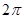 -периодической функции
-периодической функции 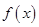 в ряд вида:
в ряд вида:

где 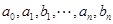 -- некоторые числа.
-- некоторые числа.
Такие ряды называются тригонометрическими, а числа 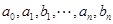 их коэффициентами.
их коэффициентами.
Член 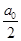 называется свободным членом (в виде
называется свободным членом (в виде 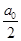 он берется для удобства).
он берется для удобства).
Определение. Тригонометрическим рядом Фурье для функции 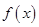 на отрезке
на отрезке 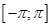 называется ряд вида
называется ряд вида 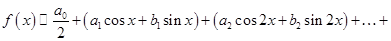
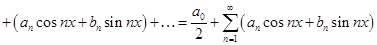 ,
,
коэффициенты которого, называемые коэффициентами Фурье для функции 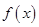 , вычисляются по следующим формулам:
, вычисляются по следующим формулам:
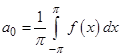 ;
;
Условия, которые достаточно наложить на функцию 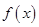 для того, чтобы её ряд Фурье сходился во всём промежутке разложения, определяются теоремой Дирихле:
для того, чтобы её ряд Фурье сходился во всём промежутке разложения, определяются теоремой Дирихле:
Если функция 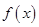 , заданная на отрезке
, заданная на отрезке 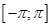 , удовлетворяет в этом промежутке условиям Дирихле, т.е.
, удовлетворяет в этом промежутке условиям Дирихле, т.е.
1) непрерывна за исключением только конечного числа точек разрыва I рода;
2) имеет конечное число экстремумов,
то ряд Фурье этой функции сходится на всём отрезке 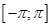 и сумма этого ряда:
и сумма этого ряда:
равна 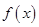 во всех точках непрерывности данной функции, лежащих внутри промежутка
во всех точках непрерывности данной функции, лежащих внутри промежутка 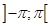 :
: 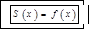 ;
;
|
|
равна 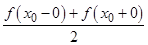 во всех точках разрыва:
во всех точках разрыва: 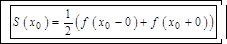 ;
;
равна 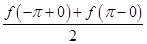 на концах промежутка:
на концах промежутка: 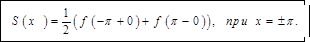
Так как члены ряда – функции периодические с периодом 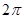 , то из сходимости ряда на отрезке
, то из сходимости ряда на отрезке 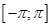 вытекает его сходимость на всей числовой оси, причем сумма этого ряда является периодической функцией с тем же периодом
вытекает его сходимость на всей числовой оси, причем сумма этого ряда является периодической функцией с тем же периодом 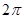 .
.
Тогда для того, чтобы ряд Фурье функции 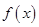 сходился именно к этой функции на всей числовой оси, надо и её считать периодической с периодом
сходился именно к этой функции на всей числовой оси, надо и её считать периодической с периодом 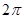 .
.
Разложение функции в ряд Фурье
Рассмотрим ряд вида
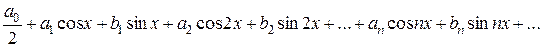
Числа 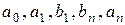 - называют коэффициентами тригонометрического ряда или его можно записать в виде
- называют коэффициентами тригонометрического ряда или его можно записать в виде 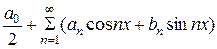
Допустим, что функция f (x) разлагается в тригонометрический ряд 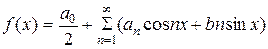
Если периодическая функция f(x) с периодом  является суммой равномерно сходящегося на
является суммой равномерно сходящегося на  тригонометрического ряда (49), то коэффициенты этого ряда определяются по формулам:
тригонометрического ряда (49), то коэффициенты этого ряда определяются по формулам:
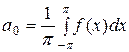 ,
, 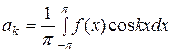 ,
, 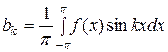 .
.
Данные коэффициенты называют коэффициентами Фурье, а тригонометрический ряд 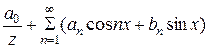 , коэффициенты которого определяются по формулам Фурье, называю рядом Фурье.
, коэффициенты которого определяются по формулам Фурье, называю рядом Фурье.
Ряды Фурье для чётных и нечётных функций.
Если f (x) – чётная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
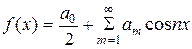 , где
, где 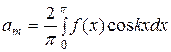 .
.
Если требуется разложить в ряд Фурье нечетную функцию, 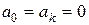 ,
, 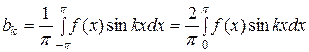 .
.
Ряд Фурье для нечетной функции имеет вид: 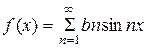 .
.
Если функция f (x) – задана на 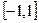 , где l – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряд Фурье:
, где l – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряд Фурье:
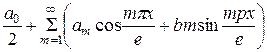 ,
,
где 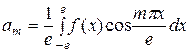 ,
, 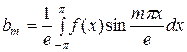 .
.
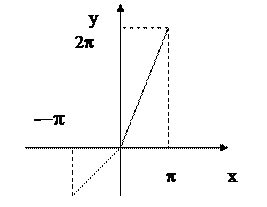
Пример 12. Разложить в ряд Фурье функцию f(x) = 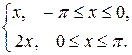 определенную в интервале (- p; p).
определенную в интервале (- p; p).
Решение. Вычислим коэффициенты Фурье функции f(x).
 а 0 =
а 0 = 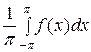 =
= 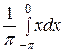 +
+ 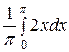 =
=
= 
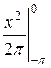 +
+ 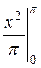 = -
= - 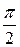 + p =
+ p = 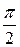 .
.
|
|
а n = 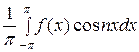 =
= 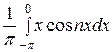 +
+
+ 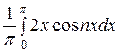 =
= 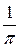 (I1 + I2). Интегралы I1, I2 интегрируем по частям: I1 =
(I1 + I2). Интегралы I1, I2 интегрируем по частям: I1 = 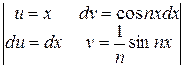 =
= 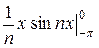 -
-
- 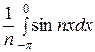 =
= 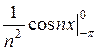 =
= 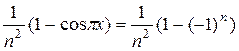 .
.
I2 = 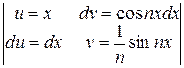 =
= 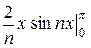 -
- 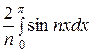 =
= 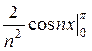 =
=
=  =
= 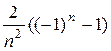 . Итак, аn =
. Итак, аn = 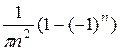 +
+ 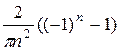 =
=
= 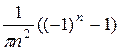 . Аналогично вычисляем коэффициент bn:
. Аналогично вычисляем коэффициент bn:
bn = 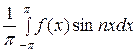 =
= 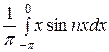 +
+ 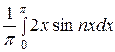 =
=
= 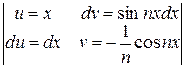 =
= 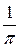 (
(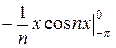 +
+ 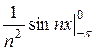 ) +
) +
+ 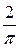 (
(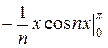 +
+ 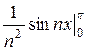 ) =
) = 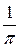 (-
(- 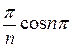 -
- 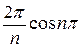 )=
)= 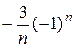 .
.
Следовательно, ряд Фурье для функции f(x) имеет вид:
f(x) = 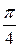 +
+ 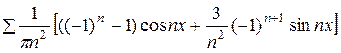 .
.