Любое составное число можно разложить на простые множители. На самом деле, мы этим уже занимались, когда изучали тему замены в выражениях. Если помните, мы сказали, что любой параметр в выражении можно заменить на тот же, но записанный в другом виде.
А здесь речь идёт о том, что любое число можно разложить на множители. Другими словами, представить число в виде произведения нескольких множителей.
Рассмотрим число 4. Разложим его на множители. Для этого, надо собрать это число из других чисел, при этом соединяться они должны знаком умножить (×). Очевидно, 4 состоит из множителей 2 и 2:
2 × 2 = 4
Разложим на множители число 6. Шесть можно собрать из чисел 2 и 3:
2 × 3 = 6
Разложим на множители число 8. Восемь можно собрать из чисел 2 и 4, при этом последняя четвёрка тоже раскладывается на множители 2 и 2. Поэтому, вместо последней четвёрки записываем её разложение:
2 × 2 × 2 = 8
Большие числа раскладываются таким же образом. Сначала их раскладывают на более маленькие числа, затем на более маленькие, до тех пор пока каждое число не станет простым. Например, разложим число 180 на множители. 180 это два множителя 18 и 10:
18 × 10 = 180
Теперь, раскладываем множители 18 и 10 также на другие множители по отдельности:
3 × 6 = 18
5 × 2 = 10
Теперь, раскладываем выделенную синюю шестерку. Это последнее число, которое можно разложить на множители:
2 × 3 = 6
Теперь, собираем все разложенные множители вместе:
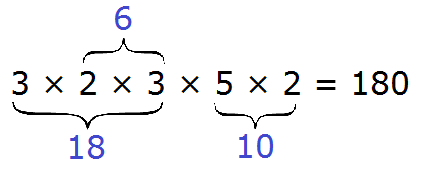
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Этот метод заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим методом, используют признаки делимости, такие как признаки делимости на 2, на 3, на 5 и т.д.
К примеру, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180:

Теперь применяем признаки делимости. В первую очередь, проверяем делится ли 180 на 2. Если делится, то записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2, и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
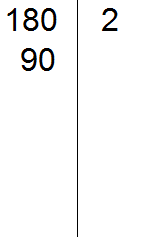
Теперь делим 90. Снова применяем признаки делимости. Проверяем в первую очередь делится ли 90 на 2.
90 делится на 2, поскольку оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем в первую очередь делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 на 3 делится, поскольку сумма цифр 45 это 4 + 5 = 9, а девять делится на три. Записываем тройку справа от вертикальной линии:
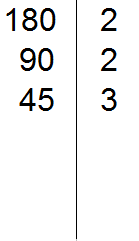
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
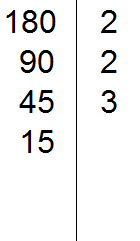
Теперь делим 15. В первую очередь проверяем делится ли 15 на 2.
15 на 2 не делится. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 15 это 1 + 5 = 6, а шесть делится на три. Записываем тройку справа от вертикальной линии:
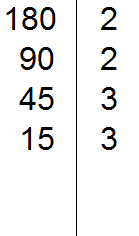
Делим 15 на эту 3, получаем пятое делимое 5. Записываем эту пятёрку слева от вертикальной линии:
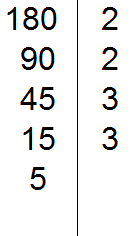
Теперь делим 5. В первую очередь проверяем делится ли 5 на 2.
5 на 2 не делится. Тогда проверяем делится ли 5 на 3.
5 на 3 не делится. Тогда проверяем делится ли 5 на 5.
5 на 5 делится. Записываем эту пятёрку справа от вертикальной линии:

Делим 5 на эту 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Теперь просто переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
