| Нормальная форма логической функции – если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией. | |
| Элементарная конъюнкция – конъюнкция конечного множества логических переменных и их инверсий. К ней относят константу единицы, выражения, состоящие из одной переменной. | Элементарная дизъюнкция – дизъюнкция конечного множества логических переменных и их инверсий. |
| Ранг элементарной конъюнкции или дизъюнкции – число аргументов ее образующих. Переменные входящие в элементарную конъюнкцию и дизъюнкцию – термы. Ранг терма – количество переменных, входящих в данный терм. | |
| Примеры | |
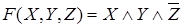Элементарная конъюнкция третьего порядка
| 
Элементарная дизъюнкция второго порядка
|
| Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операциями конъюнкции. | Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операциями дизъюнкции. |
| Любая переключательная функция имеет несколько ДНФ и КНФ. Всякое выражение булевой алгебры можно преобразовать в эквивалентную ему ДНФ и КНФ. Для заданной функции ДНФ не будет единственной. ДНФ и КНФ не дают однозначного представления функции. Для этого существуют совершенные формы. Всякое выражение булевой алгебры может быть представлено в СДНФ и СКНФ. Произвольная булева функция может быть представлена единственной СДНФ или СКНФ. | |
| Примеры | |
| 
|
| Совершенная конъюнктивная нормальная форма (СКНФ): 1) нет двух элементарных дизъюнкций; 2) ни одна элементарная дизъюнкция не содержит двух одинаковых переменных; 3) ни одна элементарная дизъюнкция не содержит переменную вместе с ее инверсией; 4) все дизъюнкции имеют один и тот же ранг. | Совершенная дизъюнктивная нормальная форма (СДНФ) 1)Нет двух одинаковых термов 2)Ни один терм не содержит двух одинаковых переменных 3)Ни один терм не содержит вместе с переменной и ее отрицание |
| Алгоритм образования СКНФ и СДНФпо таблице истинности | |
| 1. Выделить в таблице истинности все строки, в которых функция принимает значения 0. | 1. Выделить в таблице истинности все строки, в которых функция принимает значения 1. |
| 2. Для каждого выбранного набора записать элементарные дизъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается сама переменная, б) если значение переменной равно 1, то записывается инверсия этой переменной. | 2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается инверсия этой переменной, б) если значение переменной равно 1, то записывается сама переменная. |
| 3. Соединить элементарные дизъюнкции знаком конъюнкции. | 3. Соединить элементарные конъюнкции знаком дизъюнкции. |
Пример создания СКНФ
Исходная таблица
| X | Y | Z | F |
1. Выделить в таблице истинности все строки, в которых функция принимает значения 0.
| X | Y | Z | F |
2. Для каждого выбранного набора записать элементарные дизъюнкции, содержащие переменные
a. если значение переменной равно 0, то записывается сама переменная,
b. если значение переменной равно 1, то записывается инверсия этой переменной.
| X | Y | Z | F | ||
| |||||
| |||||
| |||||
| |||||
3. Соединить элементарные дизъюнкции знаком конъюнкции.
Конституента единицы – логическая (переключательная) функция от n аргументов, принимающая значение единицы только на одном наборе аргументов. Среди переключательных функций от двух переменных конституент единицы K – 4.
K1 = f4, K2 = f2, K3 = f1
Конституента нуля – логическая (переключательная) функция от n аргументов, принимающая значение нуля только на одном наборе аргументов. Среди переключательных функций от двух аргументов конституент нуля R – 4. R0 = f7, R1 = f11, R2 = f13, R3 = f14