Лекции 4,5. Случайные процессы и их основные статистические характеристики

План.

1.Понятие случайного процесса.

2.Реализации и сечения случайного процесса.

3.Функции распределения и плотности вероятности СП.

4.Белый шум и марковский СП.

5.Статистические характеристики СП.

 

Функцию, значение которой при каждом значении независимой пере­менной является случайной величиной, называют случайней функцией. Случайные функции, для которых независимой переменной является время, называют случайными процессами или стохастическими про­цессами. Поскольку в автоматических системах управления процессы протекают во времени, то в дальнейшем будут рассматриваться только случайные процессы.

Случайный процесс X(t} не есть определенная кривая, он является множеством определенных кривых X_i{t), где i =1, 2,..., п, получаемых в результате отдельных опытов (рис. 4.1). Каждую кривую этого множества называют реализацией случайного процесса. Сказать заранее, по какой из реализации пойдет процесс, невозможно.

Рассмотрим, например, случайный дрейф на выходе усилителя по­стоянного тока при входном напряжении, равном нулю. Чтобы изу­чить характеристики дрейфа, можно взять, например, п одинаковых усили­телей, поместить их в одинаковые условия работы, одновременно включить и получить п осциллограмм дрейфа на выходах усилителей. Совокупность всех осциллограмм образует случайный процесс X(t}, a каждая из осциллограмм является конкретной реа­лизацией x,(f) случайного процесса.

Для любого фиксиро­ванного момента времени, например t = t_i, реализа­ция случайного процесса Xi(t_i} представляет собой конкретную величину, зна­чение же случайной функ­ции X(/i) является случай­ной величиной,называемой сечением случайного про­цесса в момент времени tx. Поэтому нельзя утвер­ждать, что случайный про­цесс в данный момент времени имеет такое-то детерминированное значение, можноговоритьлишь о вероятности того, что в данный момент времени значение слу­чайного процесса как случайной величины будет находиться в оп­ределенных пределах.

Статистические методы изучают не каждую из реализации x,{t), образующих множество X(t}, а свойства всего множества в целом при помощи усреднения свойств входящих в него реализации. Поэтому при исследовании автоматической системы управления судят о ее поведе­нии не по отношению к какому-либо определенному воздействию, пред­ставляющему заданную функцию времени, а по отношению к целой совокупности воздействий.

Рис 4.1

 

Как известно, статистические свойства случайной величины х определяют по ее функции распределения (интегральному закону распределения) F(x) или плотности вероятности (дифференциальному закону распределения) w(x).

Случайные величины могут иметь различные законы распределения: равномерный, нормальный, экспоненциальный и др. Во многих зада­чах автоматического, управления очень часто приходится иметь дело с нормальным законом распределения (или законом Гаусса), который получается, если случайная величина определяется суммарным эффек­том от действия большого числа различных независимых факторов.

Рис 4.2 а,б

Для случайного процесса также вводят понятие функции распределения F(x, t) и плотности вероятности и>(х, /), которые зависят от фиксированного момента времени наблюдения t иот некоторого выбранного уровня х, т. е. являются функциями двух переменных х и t.

Рассмотрим случайную величину X(t_i), т. е. сечение случайного процесса в момент времени t_i. Одномерной функцией распределения (функцией распределения первого порядка) случайного процесса X(t) называют вероятность того, что текущее значение случайного процесса X(t_i) в момент времени t_i не превышает некоторого заданного уровня (числа) X_i, т. е.

Если функция F_i(X_i, t_i) имеет частную производную по X_i, т. е.

то функцию w_i(X_i, t_i) называют одномерной плотностью вероятности (плотностью вероятности первого порядка) случайного процесса. Ве­личина

представляет собой вероятность того, что X(t) находится в момент вре­мени t == t_i в интервале от X_i до X_i + dx_i.

В каждые отдельные моменты времени t ₁, t ₂ ,..., t_n наблюдаемые слу­чайные величины (сечения случайного процесса) X(t_i), X (t ₂),..., X(t_n) будут иметь свои, в общем случае разные, одномерные функции распределения F ₁(x ₁, t ₁), F ₁(x ₂, t ₂) ,..., F ₁(x_n, t_n) и плотности вероятности w ₁(x ₁, t ₁), w ₁(x ₂, t ₂) ,..., w ₁(x_n, t_n).

Функции F_i (x, t) и w (x, t) являются простейшими статистическими характеристиками случайного процесса. Они характеризуют случай­ный процесс изолированно в отдельных его сечениях, не раскрывая взаимной связи между сечениями случайного процесса, т. е. между возможными значениями случайного процесса в различные моменты времени.

Знания этих функций еще недостаточно для описания случайного процесса в общем случае. Необходимо охарактеризовать также взаим­ную связь случайных величин в различные произвольно взятые моменты времени.

Рассмотрим теперь случайные величины X (t ₁) и Х (t ₂), относящиеся к двум разным моментам времени t ₁ и t ₂ наблюдения случайного процесса.

Вероятность того, что X (t) будет не больше x ₁ при t = t ₁ и не боль­ше x ₂ при t = t ₂, т. е.

называют двумерной функцией распределения (функцией распределения второго порядка). Если функция F ₂(x ₁, t ₁; x ₂, t ₂) имеет частные произ­водные по x ₁ и x ₂, т.е.

то функцию w ₂(x ₁, t ₁; x ₂, t ₂) называют двумерной плотностью вероятности (плотностью вероятности второго порядка.) Величина

равна вероятности того, что X (t) при t == t ₁ будет находиться в интер­вале от x ₁ до x ₁+ dx ₁, а при t = t ₂ в интервале от x ₂ до x ₂+ dx ₂.

Аналогично можно ввести понятие о п-мерной функции распре­деления:

Если функция F_n имеет частные производные по всем аргументам

x ₁, x ₂,..., x_n, т. е.

то функцию w_n называют п-мерной плотностью вероятности.

Чем выше порядок п, тем полнее описываются статистические свойства случайного процесса. Зная п-мерную функцию распреде­ления, можно найти по ней одномерную, двумерную и другие (вплоть до (n-1)-й) функции распределения более низкого порядка. Однако многомерные законы распределения случайных процессов являются сравнительно громоздкими характеристиками и с ними крайне трудно оперировать на практике. Поэтому при изучении случайных процессов часто ограничиваются случаями, когда для описания случайного про­цесса достаточно знать только его одномерный или двумерный закон распределения.

Примером случайного процесса, который полностью характеризуется одно­мерной плотностью вероятности, является так называемый чистый случайный процесс, или белый шум. Значения Х (t) в этом процессе, взятые в разные момен­ты времени t, совершенно независимы друг от друга, как бы близко ни были вы­браны эти моменты времени. Это означает, что кривая белого шума содержит всплески, затухающие за бесконечно малые промежутки времени. Поскольку значения X (t), например, в моменты времени t ₁ и t ₂ независимы, то вероятность совпадения событий, заключающихся в нахождении Х (t) между x ₁ и x ₁+ dx ₁ в момент времени t ₁ и между x ₂ и x ₂+ dx ₂ в момент t ₂, равна произведению вероят­ностей каждого из этих событий, поэтому

Н вообще для белого шума

т. е. все плотности вероятности белого шума определяются из одномерной плотности вероятности.

Для случайных процессов общего вида, если известно, какие значения при­няла величина Х (t_k) в момент времени t_k, тем самым имеем некоторую информа­цию относительно Х (t_m), где m > k, так как величины Х (t_m) и Х (t_k), вообще го­воря, зависимы. Если кроме Х (t_k) известна Х (t_l), где l < k, то информация о X (t_m) еще более увеличивается. Таким образом, увеличение наших знаний о поведении процесса до момента t_k приводит к тому, что увеличивается информа­ция о Х (t_m).

Однако существует особый класс случайных процессов, впервые исследо­ванных известным математиком А.А. Марковым и называемых марковскими слу­чайными процессами, для которых знание значения процесса в момент t_k уже со­держит в себе всю информацию о будущем ходе процесса, какую только можно извлечь из поведения процесса до этого момента. В случае марковского случай­ного процесса для определения вероятностных характеристик процесса в момент времени t_m достаточно знать вероятностные характеристики для любого одного предшествующего момента времени, например непосредственно предшествующего момента времени t_k. Знание вероятностных характеристик процесса для других предшествующих значений времени, например t_l, не прибавляет информации, необходимой для нахождения Х (t_m).

Дли марковского процесса справедливо следующее соотношение:

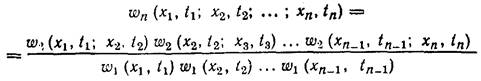
т. е. все плотности вероятности марковского процесса определяютсяиз двумер­ной плотности вероятности. Другими словами, марковские случайные процессы полностью характеризуются двумерной плотностью вероятности.

Понятие о функции распределения и плотности вероятности слу­чайного процесса обычно используют при теоретических построениях и определениях. В практике исследования автоматических систем уп­равления широкое распространение получили сравнительно более простые, хотя и менее полные характеристики случайных процессов, аналогичные числовым характеристикам случайных величин. Приме­рами таких характеристик служат рассматриваемые ниже: математи­ческое ожидание, дисперсия, среднее значение квадрата случай­ного процесса, корреляционная функция, спектральная плотность и другие.

Математическим ожиданием (средним значением) m_x (t) случайного процесса X(t) называют величину

где w ₁ (x, t) — одномерная плотность вероятности случайного процесса X(t).

Математическое ожидание случайного процесса X(t) представляет собой некоторую неслучайную (регулярную) функцию времени m_x (t), около которой группируются и относительно которой колеблют­ся все реализации данного случайного процесса (рис. 3).

Математическое ожидание случайного процесса в каждый фиксиро­ванный момент времени t_k равно математическому ожиданию соответ­ствующего сечения случайного процесса X (t_k) и представляет собой операцию вероятностного усреднения случайной величины X (t_k), при котором каждое возможное значение для случайной величины х принимается с весом, равным элементу вероятности w ₁ (x, t_k)dx [см.(6)]. Математическое ожидание называют средним значением случайного процесса по множеству (средним по ансамблю, статистическим средним), поскольку оно представляет собой вероятностно усредненное значение бесконечного множества реализации случайного процесса.

Средним значением квадрата случайного процесса называют ве­личину

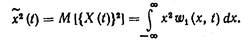(4.1)

Рис 4.3. а, б

 

Иногда вводят в рассмотрение так называемый центрированныйслучайный процесс X⁰ (t), под которым понимают отклонение случайного процесса X (t) от его среднего значения m_x (t), или

(4.2)

Тогда случайный процесс X{t) можно рассматривать как сумму двух составляющих: регулярной составляющей, равной математическому

ожиданию m_x (t), и центрированной случайной составляющей X⁰(t), т. е.

(4.3)

Очевидно, что математическое ожидание центрированного случайного процесса равно нулю:

(4.4)

Для того чтобы каким-то образом учесть степень разбросанности реализации случайного процесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, которая равна мате­матическому ожиданию квадрата центрированного случайного про­цесса:

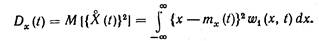(4.5)

Дисперсия случайного процесса является неслучайной (регулярной) функцией времени D_x(t), значение которой в каждый момент времени t_k равно дисперсии соответствующего сечения Х(t_k) случайного процесса.

Легко показать,что математическое ожидание m_x (t), дисперсия D_x (t) и среднее значение квадрата x^~2 (t) случайного процесса, имею­щие размерность квадрата случайной величины, связаны соотношением

(4.6)

Из (4.6) видно, что среднее значение квадрата случайного про­цесса x^~2 (t) в определенной мере учитывает и среднее значение случай­ного процесса, и степень рассеяния его реализации относительно этого среднего значения, поэтому оно широко используется в качестве оцен­ки точности систем автоматического управления.

На практике часто бывает удобно пользоваться статистическими характеристиками случайного процесса, имеющими ту же размер­ность, что и сама случайная величина. К таким характеристикам от­носят:

среднее квадратическое значение случайного процесса

(4.7)

равное арифметическому значению квадратного корня из среднего зна­чения квадрата случайного процесса;

среднее квадратическое отклонение случайного процесса

(4.8)

равное арифметическому значению квадратного корня из дисперсии случайного процесса.

Из (4.7) и (4.8) видно,что среднее квадратическое значение x_с.к (t) и среднее квадратическое отклонение s_x (t) случайного процесса в общем случае не совпадают.

В заключение заметим, что хотя ни математическое ожидание, ни дисперсия случайного процесса ни в какой мере не характеризуютстепень статистической зависимости между сечениями случайно­го процесса в различные моменты времени, знания этих характеристик часто достаточно для решения многих задач теории автоматического управления.