Уравнения, содержащие неизвестное под знаком модуля
Уравнения вида 
Наиболее рациональный путь решения – переход к совокупности 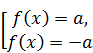 .
.
Уравнения вида 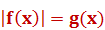
Такие уравнения можно двумя способами заменить равносильными условиями:  и
и 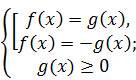 .
.
Выбор способа замены зависит от того, какое и неравенств 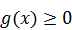 или
или 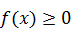 решить легче.
решить легче.
Пример 1. Решить уравнение 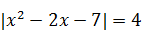 .
.
Решение. Исходное уравнение равносильно совокупности 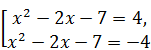 Û
Û 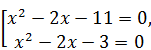 .
.
Решая эти уравнения, получим корни х = ‑ 1; х =3; х =1±2 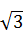
Ответ: ‑ 1; 3; 1±2 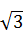
Пример 2. Решить уравнение 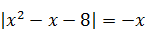 .
.
Решение. Исходное уравнение равносильно системе 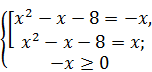 Û
Û 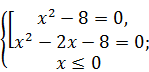 .
.
Решая эти уравнения, получим корни х = ‑ 2; х =4; х =±2 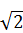 . Но условию
. Но условию 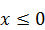 удовлетворяют только числа – 2 и ‑ 2
удовлетворяют только числа – 2 и ‑ 2 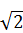 .
.
Ответ: ‑ 2; ‑ 2 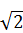
Пример 3. Решите уравнение 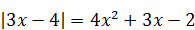 .
.
Решение. Поскольку в уравнении функция, стоящая под знаком модуля, проще, то лучше записать уравнение как совокупность двух систем:
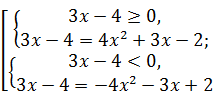 Û
Û 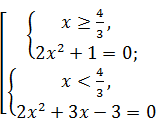 .
.
Уравнение из первой системы совокупности корней не имеет. Решением второй системы является 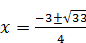 .
.
Ответ: 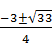
Уравнения вида 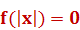
Уравнения этого вида можно решать, используя замену 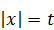 .
.
Пример 4. Решить уравнение 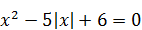 .
.
Решение. Так как 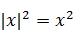 , данное уравнение примет вид:
, данное уравнение примет вид: 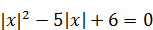 .
.
Сделаем замену 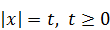 , получим новое уравнение
, получим новое уравнение 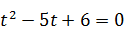 , которое имеет два положительных корня t =2; t =3. Значит, | x |=2: | x |=3, откуда x =±2, x =±3.
, которое имеет два положительных корня t =2; t =3. Значит, | x |=2: | x |=3, откуда x =±2, x =±3.
Ответ: ‑ 2; 2; ‑ 3; 3
Пример 5. Решить уравнение 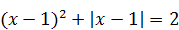 .
.
Решение. Так как 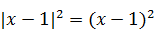 , данное уравнение примет вид:
, данное уравнение примет вид: 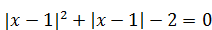 . Сделаем замену
. Сделаем замену 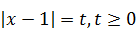 , получим новое уравнение
, получим новое уравнение 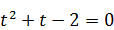 ; t = ‑ 2; t =1. Однако t = ‑ 2 не удовлетворяет условию
; t = ‑ 2; t =1. Однако t = ‑ 2 не удовлетворяет условию 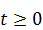 .
.
Получим уравнение 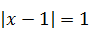 . Откуда
. Откуда 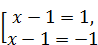 Û
Û 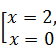 .
.
Ответ: 0; 2
Уравнения, решение которых основано на свойствах модуля
Пример 6. Решить уравнение 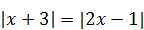 .
.
Решение. Возведем обе части уравнения в квадрат: 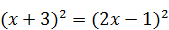 Û
Û 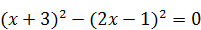 .
.
Используя формулу разности квадратов, разложим левую часть на множители: 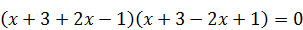 Û
Û 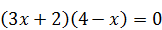 . Откуда х =
. Откуда х = 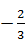 ; х =4.
; х =4.
Ответ: 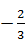 ; 4
; 4
Уравнения вида 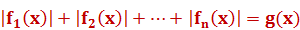
При решении таких уравнений применяется метод интервалов:
1. определяются точки, в которых каждая из функций равна нулю;
2. найденные промежутки разбивают область определения уравнения на промежутки, на каждом из которых все функции сохраняют знак;
3. исходное уравнение решается на каждом промежутке, при этом модули опускаются с учетом знака функций на рассматриваемом промежутке;
4. объединяются решения, найденные на всех частях области определения уравнения.
Пример 7. Решите уравнение 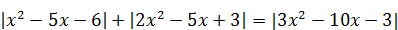 .
.
Решение. Заметим, что данное уравнение имеет вид 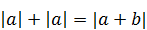 .
.
Из свойств абсолютной величины следует, что это равенство справедливо тогда и только тогда, когда ab ³0. Поэтому исходное уравнение равносильно неравенству 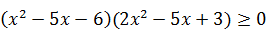 .
.
Корни трехчленов: x =6; x = ‑ 1; x =  ; x =1. Решим неравенство методом интервалов:
; x =1. Решим неравенство методом интервалов:
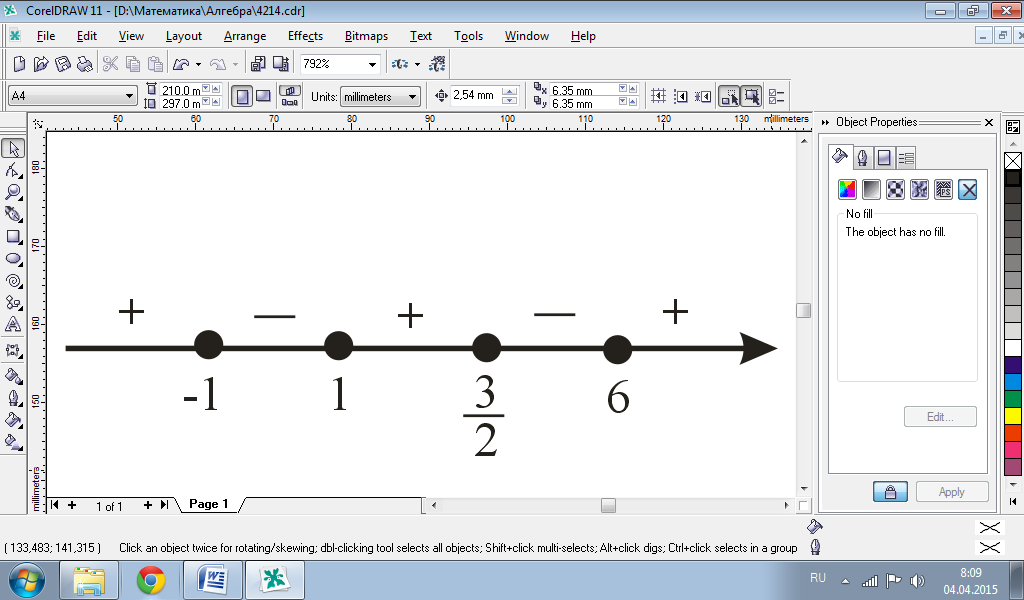
Ответ: (‑ ∞; ‑ 1]È[1;  ]È[6; +∞)
]È[6; +∞)
Рассмотрим уравнение: |2 ‑ x |=16 – 2|5 – x | ‑ | x |
Шаг 1. Под каждым из модулей все слагаемые расположить в порядке убывания степеней х, причем коэффициент при старшей степени х сделать положительным числом.
|2 ‑ x |=16 – 2|5 – x | ‑ | x | Û | x – 2|+| x |+2| x – 5|=16.
Шаг 2. Определить нули каждого выражения под знаком модуля, присутствующего в уравнении (неравенстве). Эти точки разбивают область определения каждого подмодульного выражения на интервала знакопостонства.
Шаг 3. Нанести нули каждого из выражений на отдельную силовую прямую и расположить все эти прямые друг под другом. Указать на прямых такие промежутки, в пределах которых все подмодульные выражения одновременно сохраняют знакопостоянство.
Для нашего примера 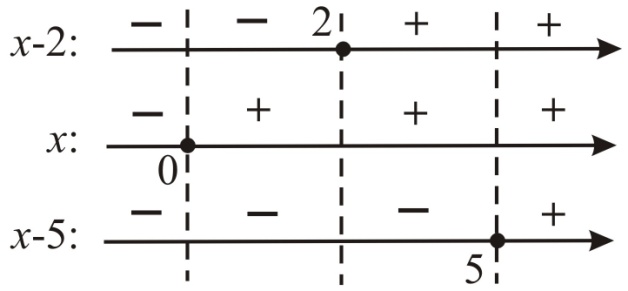
Здесь на промежутках (‑ ∞; 0], (0; 2], (2; 5], (5; +∞) все подмодульные выражения одновременно являются знакопостоянными.
Шаг 4. На каждом из полученных промежутков раскрыть модули в соответствии со знаками подмодульных выражений на этом промежутке и решить соответствующее промежутку уравнение (неравенство). Все полученные решения объединить в общий ответ.
В нашем примере:
1) 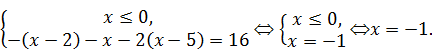
2) 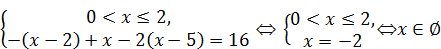 .
.
3) 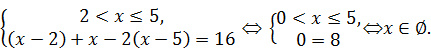
4) 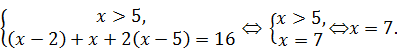
Ответ: (‑ 1; 7)
Метод интервалов выручает в следующих ситуациях:
· Под знаком модуля встречаются не только линейные функции, но квадратичные, кубические, показательные и пр.;
· Формулировка задачи не обязательно сводится к решению уравнения или неравенства.
Примеры решения задач
Пример 1. Решить уравнение | x |=3.
Решение. Это отношение геометрически означает, что расстояние от точки х до начала координат равно 3, т.е. х =3 или х = ‑ 3.
Ответ: 3; ‑ 3
Пример 2. Решить уравнение | x +5|=2.
Решение. Рассматривая | x +5| как | x – (‑ 5)| данное уравнение означает что расстояние от точки х до точки – 5 равно 2. Откладывая на числовой оси от точки – 5 отрезок длиной 2 (в обе стороны), получим – 7 и – 3.
Ответ: ‑ 7; ‑ 3
Пример 3. Решить уравнение |3 – 2 x |=1.
Решение. Преобразуем |3 – 2 x |=|2 x – 3|=|2(x – 1,5)|=2| x – 1,5|, откуда 2| x – 1,5|=1. Разделив обе части уравнение на 2, получаем | x – 1,5|=0,5. Используя числовую ось, получаем ответ х =1 или х =2.
Ответ: 1; 2
Пример 4. Решите уравнение | х +3|=2 х – 1.
Решение: х +3=0, х = ‑ 3.
1) (‑ ∞; ‑ 3) – х – 3=2 х – 1, х = 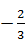 (не входит в рассматриваемый промежуток).
(не входит в рассматриваемый промежуток).
2) [ ‑ 3; +∞) х +3=2 х – 1, х =4; 4Î[ ‑ 3; +∞).
Ответ: 4
Пример 5. Решить уравнение 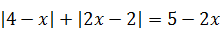
Решение. Это уравнение не приводится к виду 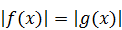 . Поэтому решим его методом интервалов, сопроводив решение маленькой, но важной «уловкой», которая поможет уменьшить количество рассматриваемых интервалов. Сначала запишем уравнение в виде:
. Поэтому решим его методом интервалов, сопроводив решение маленькой, но важной «уловкой», которая поможет уменьшить количество рассматриваемых интервалов. Сначала запишем уравнение в виде: 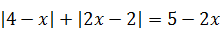 . Заметим, что сумма модулей
. Заметим, что сумма модулей 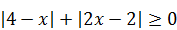 . Поэтому 5 ‑ 2 x
. Поэтому 5 ‑ 2 x 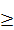 0, а значит,
0, а значит, 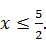
х ‑ 4: 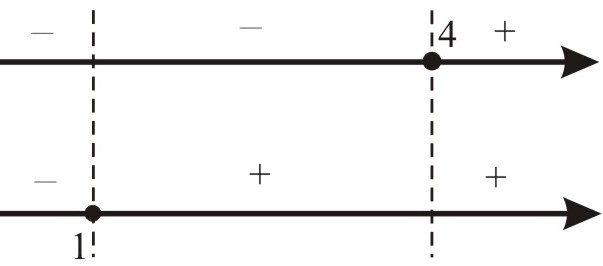
2 х – 2: 
Последнее наблюдение позволяет нам рассматривать лишь два промежутка (‑ ¥; 1] и (1; 2,5] вместо трёх: (‑ ¥; 1], (1; 4] и (4; +¥). На каждом из этих двух промежутков раскроем модули и решим соответствующие уравнения:
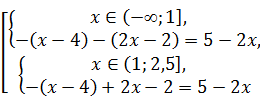 Û
Û 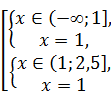 Û x =1.
Û x =1.
Ответ: 1
Пример 6. Найти количество целых чисел, принадлежащих области значений функции 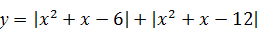 , заданной на отрезке [ ‑ 5; 5].
, заданной на отрезке [ ‑ 5; 5].
Решение. Методом интервалов раскроем модули:
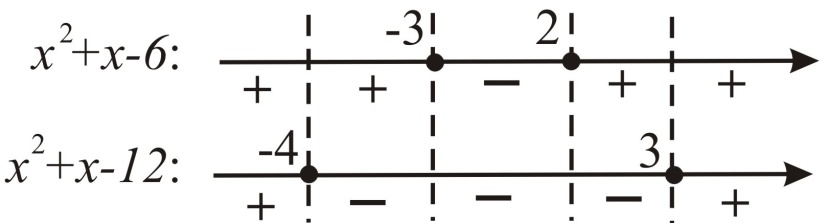
1) 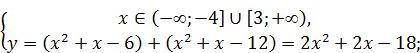
2) 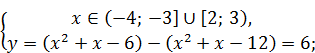
3) 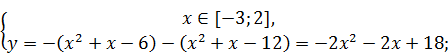
Теперь построим график исходной функции на отрезке [ ‑ 5; 5].
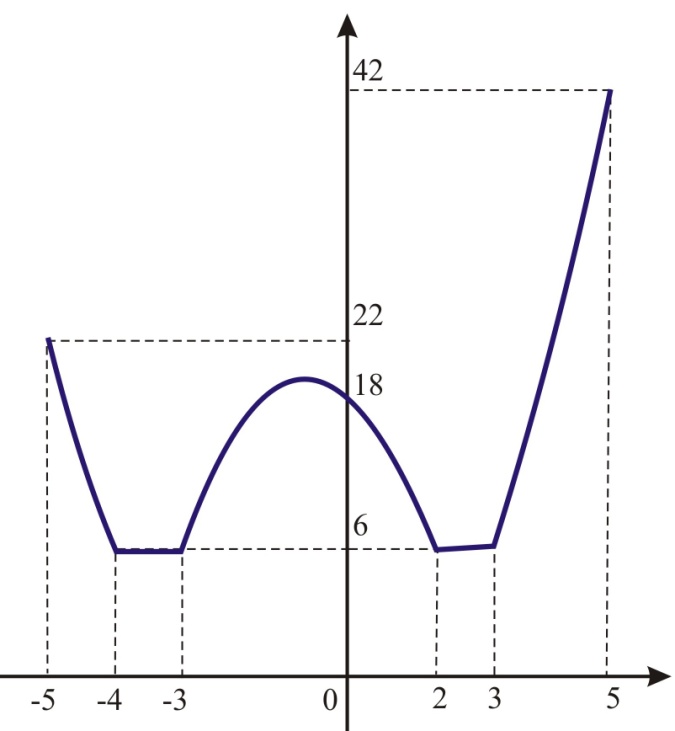
Из графика видно, что областью значений данной функции является отрезок [6; 42]. Поэтому искомое количество целых числе из отрезка [6; 42] равно 42 – 6+1=37.
Ответ: 37
Пример 7. Найти сумму корней уравнения или корень, если он единственный: 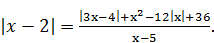
Решение. Это уравнение вполне можно было бы решить методом интервалов, раскрывая модули на каждом из четырёх промежутков: (‑ ¥; 0], 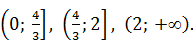
Запишем данное уравнение в виде | x ‑ 2|= 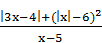 , из которого усматриваем «подсказку»: знаменатель x ‑ 5 больше нуля, поскольку неотрицательным являются числитель и левая часть уравнения. Итак, x >5, а значит подмодульные выражения x, x ‑ 2, 3 x ‑ 4 положительные и потому | x ‑ 2|= x ‑ 2, | x |= x, |3 x ‑ 4|=3 x ‑ 4.
, из которого усматриваем «подсказку»: знаменатель x ‑ 5 больше нуля, поскольку неотрицательным являются числитель и левая часть уравнения. Итак, x >5, а значит подмодульные выражения x, x ‑ 2, 3 x ‑ 4 положительные и потому | x ‑ 2|= x ‑ 2, | x |= x, |3 x ‑ 4|=3 x ‑ 4.
Таким образом, данное уравнение равносильно системе:
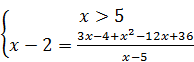 Û
Û 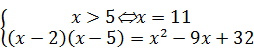 . Û
. Û 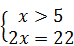 Û x =11.
Û x =11.
Ответ: 11
Пример 8. Найти максимальный корень уравнения 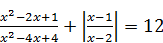 .
.
Решение: Поскольку х 2 – 2 х +1=(х – 1)2, х 2 – 4 х +4=(х – 2)2, то уравнение принимает вид: 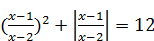 .
.
Вспоминая, что 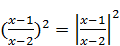 , вводим новую переменную t =
, вводим новую переменную t = 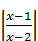 , t ³0. Данное уравнение является квадратным относительно t:
, t ³0. Данное уравнение является квадратным относительно t:
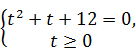 Û
Û 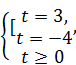 Û t =3.
Û t =3.
Возвращаясь к переменной х, получаем
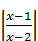 =3 Û
=3 Û 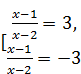 Û
Û 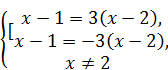 Û
Û 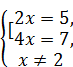 Û
Û 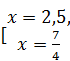 .
.
Максимальный корень уравнения – 2,5.
Ответ: 2,5
Пример 9. Найти целые решения уравнения |3 x +26|+|2 y +29|=2.
Решение. Так как х и у принимают только целые значения, то |3 x +26| и |2 y +29| будут принимать только целые неотрицательные значения, причем |2 y +29| - нечетные.
Поэтому их сумма может быть равна 2, только если 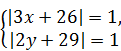 .
.
Следовательно, 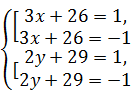 Û
Û 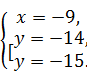
Ответ: (‑ 9; ‑ 14), (‑ 9; ‑ 15)
Пример 10. Решить уравнение 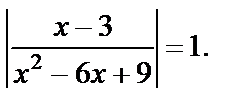
Решение. ОДЗ: х ¹3. Уравнение записывается в виде 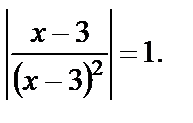
На ОДЗ можно сократить и получаем 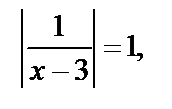 откуда
откуда 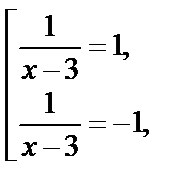 т. е.
т. е. 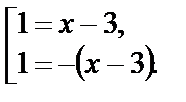 Получаем корни
Получаем корни 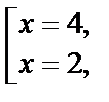 которые подходят по ОДЗ.
которые подходят по ОДЗ.
Ответ: 4; 2
Пример 11. Решить уравнение 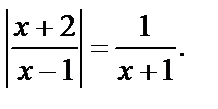
Решение. ОДЗ: х ¹±1. Оно имеет решение, если 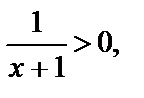 т. е. при
т. е. при 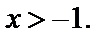 Таким образом, для
Таким образом, для  получаем:
получаем: 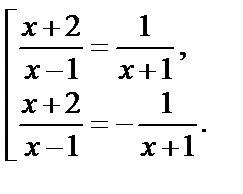
Решим отдельно полученные дробно-рациональные уравнения. Первое уравнение сводится к виду 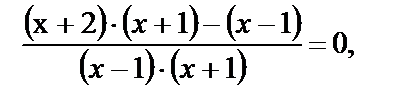 откуда
откуда 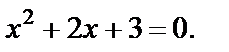
Это квадратное уравнение решений не имеет, так как 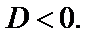
Из второго уравнения совокупности (3.13) получаем 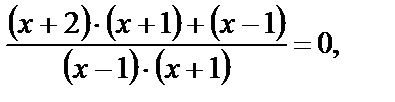 т. е.
т. е. 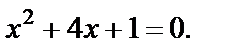
Квадратное уравнение имеет корни: 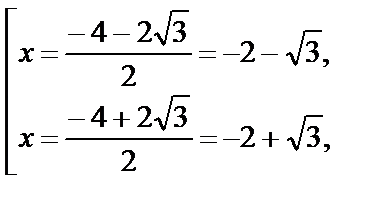 т. е. первый корень не принадлежит множеству
т. е. первый корень не принадлежит множеству 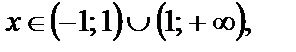 на котором решали уравнение, следовательно, ответом является только
на котором решали уравнение, следовательно, ответом является только 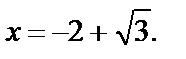
Ответ: 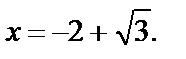
Пример 12. Решить уравнение 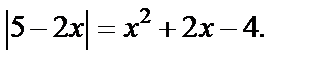
Решение. По определению модуля: 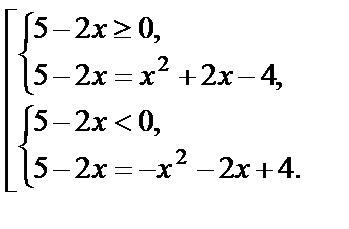
Решаем первую систему совокупности: 
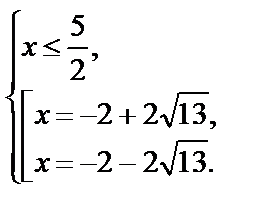
Значение 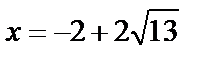 не подходит по условию
не подходит по условию 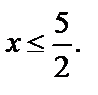 Следовательно, корнем является
Следовательно, корнем является 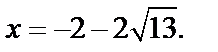
Решаем вторую систему совокупности: 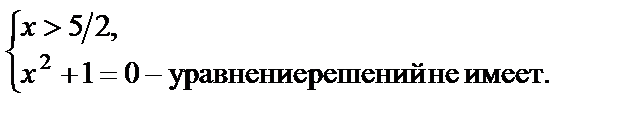
Получили ответ 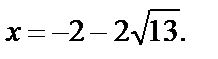
Ответ: 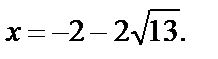
Пример 13. Решить уравнение 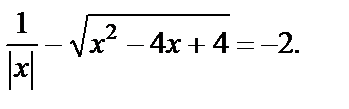
Решение. Поскольку 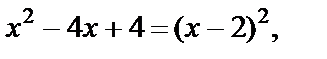 то уравнение записывается в виде
то уравнение записывается в виде 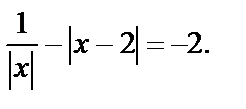 ОДЗ: х ¹0.Решим методом интервалов.
ОДЗ: х ¹0.Решим методом интервалов.
Нулями выражений, стоящих под модулем, являются 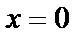 и
и 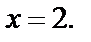 Эти значения разбивают числовую ось на три промежутка.
Эти значения разбивают числовую ось на три промежутка.
| x |
| x |
| – |
| – |
| – |
| + |
| + |
| + |
| | x | |
| | x – 2| |
Раскрыв модули на каждом из полученных промежутков, с учетом их знаков, получим совокупность систем: 
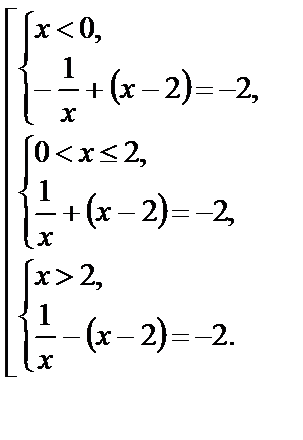
Решим отдельно системы:
I. 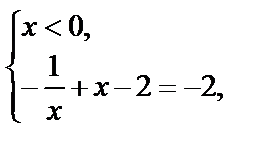
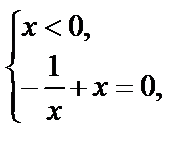
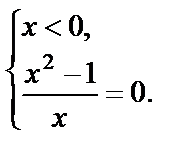
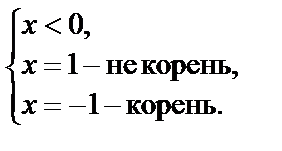
| II. 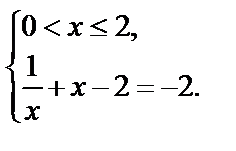
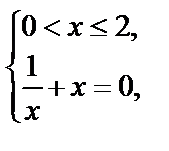

|
III. 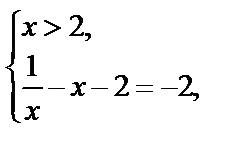
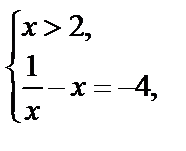
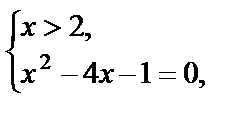
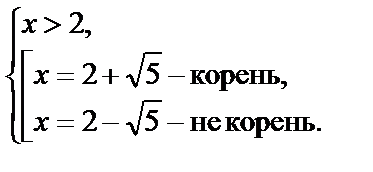
Решением данного уравнения являются значения 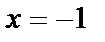 и
и 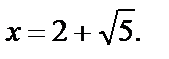
Ответ: 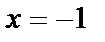 ;
; 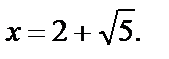
Пример 14. Решить уравнение 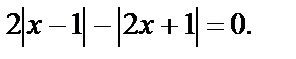
Решение. Запишем уравнение в виде 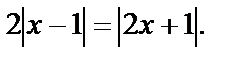
Возведем обе его части в квадрат: 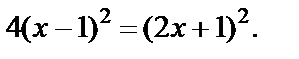 После упрощения имеем:
После упрощения имеем: 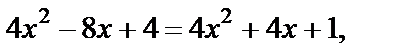 т. е.
т. е. 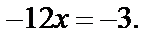 Получаем
Получаем 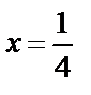 – корень.
– корень.
Ответ: 
Пример 15. Решить уравнение 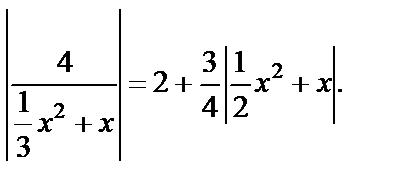
Решение. ОДЗ: 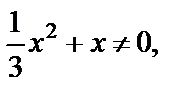 т. е.
т. е. 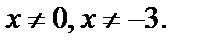
Преобразуем данное уравнение к виду 
Заменяем 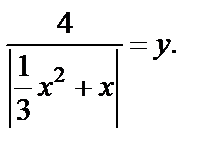 Уравнение приобретает вид
Уравнение приобретает вид 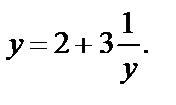
Решаем его как дробно-рациональное и получаем: 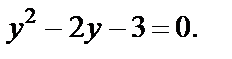
Последнее квадратное уравнение имеет корни: 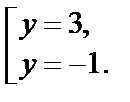
Возвращаясь к переменной х, получаем: 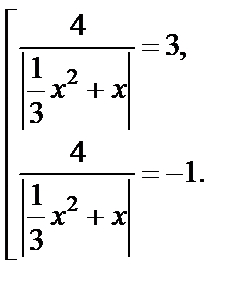
Второе уравнение совокупности решений не имеет, так как слева положительное выражение, а справа – отрицательное.
Первое уравнение совокупности сводится к I типу уравнений с модулем и равносильно совокупности при условии x ¹0 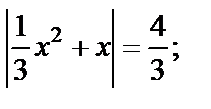
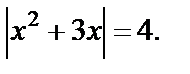
Приходим к совокупности 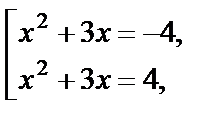 т. е.
т. е. 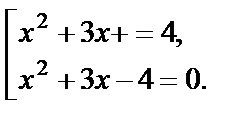
Решение имеет только второе уравнение совокупности, его корни: 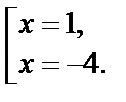 Оба они подходят по ОДЗ.
Оба они подходят по ОДЗ.
Ответ: 1; ‑ 4
Пример 16. Решить уравнение 
Решение. ОДЗ: x > ‑3. С учетом ОДЗ данное уравнение равносильно уравнению: 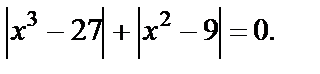
Используя свойства модуля (имеем сумму двух неотрицательных величин), получаем: 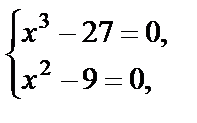
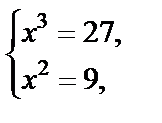
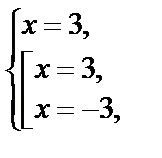 т. е х =3 – решение полученной системы, оно подходит по ОДЗ.
т. е х =3 – решение полученной системы, оно подходит по ОДЗ.
Ответ: 3
Упражнения
1. Решите уравнение:
1) 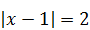
| 2) 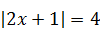
| 3) 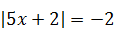
| 4) 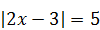
|
5) 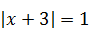
| 6) 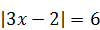
| 7) 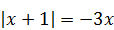
| 8) 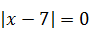
|
9) 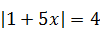
| 10) 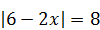
|
2. Решите уравнение:
1) 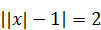
| 2) 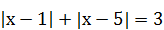
| 3) 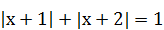
|
4) 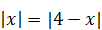
| 5) 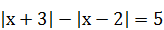
| 6) 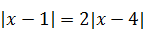
|
7) 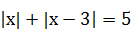
| 8) 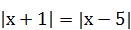
| 9) 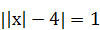
|
10) 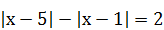
|
3. Решите уравнение:
1) 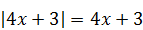
| 2) 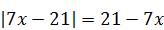
| 3) 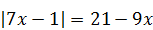
|
4) 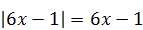
| 5) 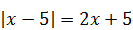
| 6) 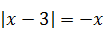
|
7) 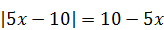
| 8) | 9) |
10) 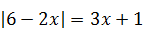
|
4. Решите уравнение:
1) 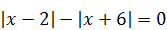
| 2) 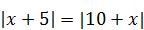
| 3) 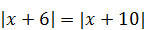
|
4) 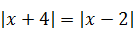
| 5) 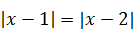
| 6) 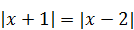
|
| 7) | 8) 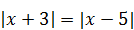
| 9) 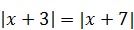
|
10) 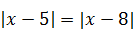
|
5. Решите уравнение:
1) 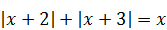
| 2) | 3) |
| 4) | 5) | 6) |
| 7) | 8) | 9) |
| 10) |
6. Решите уравнение:
1) 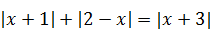
| 2) 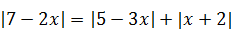
|
3) 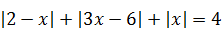
| 4) |
| 5) | 6) |
| 7) | 8) |
| 9) | 10) |
7. Найдите сумму корней уравнения:
1) 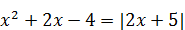
| 2) 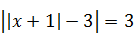
|
3) 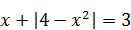
| 4) 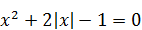
|
5) 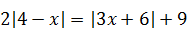
| 6) 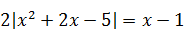
|
7) 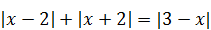
| 8) 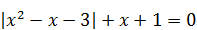
|
9) 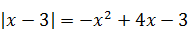
| 10) 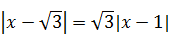
|
8. Найдите произведение корней уравнения:
1) 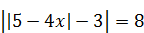
| 2) 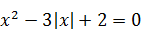
| 3) 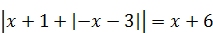
|
4) 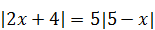
| 5) 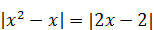
| 6) 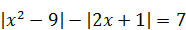
|
7) 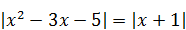
| 8) 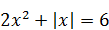
| 9) 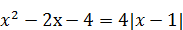
|
10) 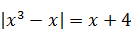
|
9. Найдите:
1) Разность между наибольшим и наименьшим корнями уравнения
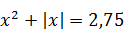
| 2) Среднее арифметическое корней уравнения
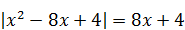
|
3) Разность между наибольшим и наименьшим корнями уравнения
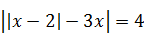
| 4) Сумму целых корней уравнения
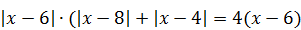
|
5) Произведение числа корней уравнения на его наибольший корень
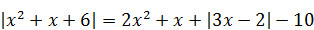
| 6) Число натуральных корней уравнения
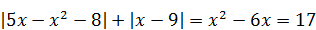
|
7) Количество корней уравнения
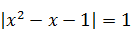
| 8) Меньший корень уравнения
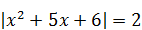
|
9) Сумму рациональных корней уравнения
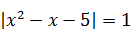
| 10) Нерациональный корень уравнения
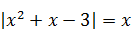
|
10. Найдите сумму целых корней уравнения:
1) 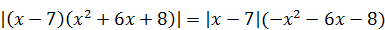
|
2) 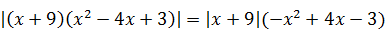
|
3) 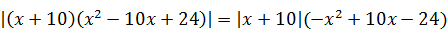
|
4) 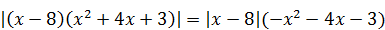
|
5) 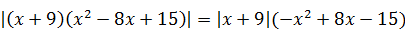
|
6) 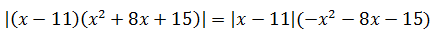
|
7) 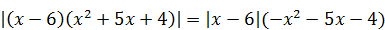
|
8) 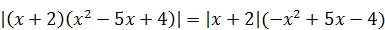
|
9) 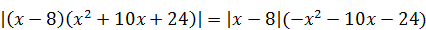
|
10) 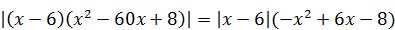
|
Дополнительные задания
1. Решите уравнение:
1) 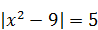
| 2) 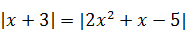
| 3) 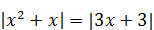
|
4) 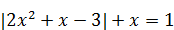
| 5) 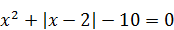
| 6) 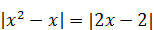
|
7) 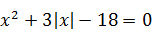
| 8) 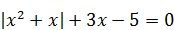
| 9) 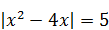
|
10) 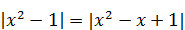
|
2. При каких значениях параметра а уравнение…
1) 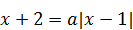 имеет единственное решение? имеет единственное решение?
|
2) 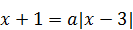 имеет единственное решение? имеет единственное решение?
|
3) 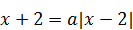 имеет единственное решение? имеет единственное решение?
|
4) 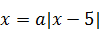 имеет единственное решение? имеет единственное решение?
|
5) 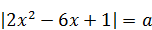 имеет три решения? имеет три решения?
|
6) 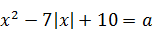 имеет три различных действительных корня? имеет три различных действительных корня?
|
7) 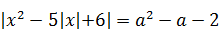 имеет четыре корня? имеет четыре корня?
|
8) 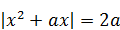 имеет три различных действительных корня? имеет три различных действительных корня?
|
9)  имеет три различных действительных корня? имеет три различных действительных корня?
|
10) 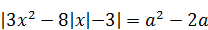 имеет шесть корней? имеет шесть корней?
|