Устройство, преобразующее дискретную информацию, в общем случае имеет п входов для входных сигналов и т выходов, с которых снимаются выходные сигналы.
Каждый из входных сигналов соответствует некоторому символу (букве) входного алфавита. В свою очередь, выходные сигналы представляют собой символы (буквы) выходного алфавита. В качестве букв этих алфавитов обычно используются двоичные цифры.
Преобразование информации в ЭВМ производится электронными устройствами (логическими схемами) двух классов: комбинационными схемами и цифровыми автоматами.
В комбинационных схемах (КС) совокупность выходных сигналов (выходное слово Y) в любой момент времени однозначно определяется входными сигналами (входным словом X), поступающими на входы в тот же момент времени (рис. 2.4, а). Реализуемый в этих схемах способ обработки информации называется комбинационным, так как результат обработки информации зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами, например, в виде таблицы. Это соответствие может быть задано и в аналитической форме с использованием булевых функций.
Другой, более сложный класс преобразователей дискретной информации составляют цифровые автоматы. Цифровой автомат в отличие от комбинационной схемы имеет некоторое конечное число различных внутренних состояний. Под воздействием входного слова цифровой автомат переходит из одного состояния в другое и выдает выходное слово. Выходное слово на выходе цифрового автомата в такте определяется в общем случае входным словом, поступившим в этот такт на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействия на автомат входных слов в предыдущие такты.
Комбинация входного слова и текущего состояния автомата в данном такте определяет не только выходное слово, но и то состояние, в которое автомат перейдет к началу следующего такта.
Цифровой автомат содержит память, состоящую из запоминающих элементов (ЗЭ) - триггеров, элементов задержки и др., фиксирующих состояние, в котором он находится. Комбинационная схема не содержит ЗЭ. Поэтому ее называют автоматом без памяти или примитивным автоматом.

Рис. 2.4. Комбинационная схема (а) и цифровой автомат (б)
Структурная схема цифрового автомата, представленная на рис. 2.4,6, содержит запоминающие элементы ЗЭ1-ЗЭк и комбинационные схемы KCI и КСII.
Состояния ЗЭ, определяющие состояние автомата, передаются в форме сигналов qj, по цепям прямой связи на входы КСII и по цепям обратной связи на входы КСI. На входы комбинационных схем поступают также сигналы Xi,...,x„ с входов автомата.
Выходное слово вырабатывается в КСII, причем входными переменными для нее служат буквы входного слова и состояния ЗЭ — состояние автомата. Выходные сигналы КСI переводят автомат (его ЗЭ) в новое состояние, при этом входными переменными для этой схемы служат буквы входного слова и состояния ЗЭ. Одновременность появления новых значений входных сигналов на всех входах устройства достигается с помощью тактирующих сигналов, называемых также синхросигналами, обеспечивающих передачу информации с ЗЭ на входы комбинационной схемы одновременно с сигналами, поступающими на ее входы с других устройств.
В ряде случаев при анализе автомата его заменяют автоматом с одним эквивалентным входом и одним эквивалентным выходом и считают, что эквивалентные входной сигнал x(t) и выходной сигнал y(t) принимают значения из соответствующим образом преобразованных алфавитов Р и S входных и выходных сигналов. Для задания цифрового автомата должны быть указаны:
1) входной алфавит P={р1, р2,…,PN}',
2) выходной алфавит S={s1, s2,...,sm};
3) алфавит состояний Q={Qo, Q1, …,Qr}',
4) начальное состояние автомата Qo',
5) функции перехода A {Q,, х) и выходов В (Q,, х), однозначно определяющие зависимость соответственно состояния автомата Q(t+1) в такте (t+1) и выходного сигнала y(t) от состояния автомата Q(t) и входного сигнала x(t) в такте t.
Используя функции переходов и выходов, можно поведение автомата описать выражениями
Q (t + 1) = A[ Q (t), x(t)]; (2.1)
y(t) = В [Q (t), x(t)], (2.2)
где t=0, 1, 2...; Q(0)=Qo.
Выражениям (2.1) и (2.2) соответствует автомат, выходной сигнал которого зависит от состояния автомата и от сигнала на его входе. Такой автомат называется автоматом Мили.
В устройствах ЭВМ широко применяются и так называемые автоматы Мура, у которых выходной сигнал y(t) в такте t зависит исключительно от состояния автомата Q (t) в этом такте и не зависит от входного сигнала x(t).
Функционирование автомата Мура описывается выражениями
Q{1+t)= A[ Q(t), x(t)]; (2.3)
y(t)=B[Q(t)], (3.4)
где t=0, 1, 2...; Q(0)=Qo.
Функции переходов и выходов могут задаваться различными способами, например в форме таблиц или с помощью графов. При задании в виде графов состояния автомата представляются вершинами, а переходы из состояния в состояние - дугами.
На дугах указываются значения входных сигналов, вызывающих соответствующие переходы. Выходные сигналы автомата Мура указываются рядом с вершинами графа. Выходные сигналы автомата Мили, вырабатываемые перед переходом, указываются на соответствующих дугах.
В теории автоматов вводятся понятия полной системы переходов и полной системы выходов автомата. Если для двух любых состояний Qi и Qj автомата имеется входной сигнал, переводящий автомат из состояния Qi, в Qj, то такой автомат называется автоматом с полной системой переходов. Автомат Мура имеет полную систему выходов, если выходные сигналы различны для всех его состояний.
При построении узлов ЭВМ, являющихся цифровыми автоматами, в качестве запоминающих элементов (элементов памяти) используются элементарные автоматы. Элементарными автоматами служат автоматы Мура с двумя состояниями, обладающие полными системами переходов и выходов.
Для описания законов функционирования комбинационных схем используется математический аппарат булевых функций.
Система булевых функций W называется функционально полной, если для любой булевой функции f(x1,...,xn) может быть построена равная ей функция путем суперпозиции функций х1,.,., xn и функций системы W, взятых в любом конечном числе экземпляров каждая.
В математической логике доказывается, что если система булевых функций содержит функции x1 x2 (конъюнкция), x1 v х2 (дизъюнкция), х (инверсия), то она является функционально полной.
Из этой системы можно исключить некоторые функции без нарушения функциональной полноты. Действительно, функциональной полнотой будут обладать также система булевых функций, x1 v х2, х и система x1 x2, х.
Функционально полной является система, состоящая из одной булевой функции И—НЕ («штрих Шеффера»): x1 x2. Функциональной полнотой обладает и система, содержащая единственную булевую функцию ИЛИ—НЕ («стрелка Пирса»): x1 v x2. Существуют и другие функционально полные системы булевых функций.
Техническим аналогом булевой функции является комбинационная схема, выполняющая соответствующее этой функции преобразование информации.
Постоянные уровни напряжения, соответствующие принятому в схеме представлению сигналов 0 и 1, могут рассматриваться как технические аналоги функции константы 0 и константы 1.
Логические операции над двоичными переменными реализуются схемами, которые называются комбинационными логическими элементами. Число входов комбинационного логического элемента соответствует числу аргументов воспроизводимых им одной или нескольких булевых функций.
Подобно тому как сложная булева функция может быть получена суперпозицией более простых функций, так и комбинационная схема строится из элементарных схем — из комбинационных логических элементов. При этом легко установить технический аналог операции суперпозиции. Последовательное соединение комбинационных схем, в том числе комбинационных логических элементов, при котором выход одной схемы соединен с входом другой схемы, соответствует подстановке в булевы функции в качестве аргументов других булевых функций. Пересоединение на входах комбинационных схем соответствует перестановке аргументов булевых функций.
Логические элементы могут быть не только комбинационными. Используются также логические элементы, реализующие функции элементарных автоматов. Схему, показывающую связи между различными логическими элементами, где сами элементы представлены условными обозначениями, называют функциональной.
При вычерчивании функциональных схем логические элементы, а часто и более крупные части схем изображают прямоугольниками, в которые вписывают символы реализуемых функций. При этом если функция реализуется при инверсных значениях некоторых входных переменных, то соответствующие входы отмечаются кружком. Выход отмечается кружком, если функция реализуется с инверсией. Примеры схем, реализующих булевы функции, даны на рис. 2.5.
Набор логических элементов для построения комбинационных схем является функционально полным, если реализуемые этими элементами булевы функции образуют функционально полную систему функций.
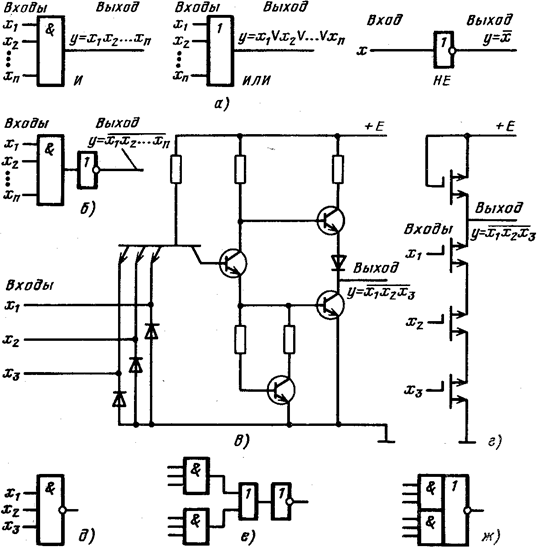
Рис. 2.5. Схемы логических элементов:
а - элементы И. ИЛИ, НЕ; б - функциональная схема элемента И-НЕ; в - принципиальная электрическая схема элемента И - НЕ транзисторно-транзисторной логики; г - принципиальная электрическая схема элемента И—НЕ на МОП-транзисторах; д - условное обозначение элемента И - НЕ; е - функциональная схема элемента И - ИЛИ -НЕ; ж- условное обозначение элемента И - ИЛИ – НЕ
Комплекс элементов обладает функциональной полнотой для построения цифровых автоматов, если он содержит функционально полный набор логических элементов для построения комбинационных схем и элементарный автомат с полной системой выходов и переходов.
В ЭВМ в качестве элементарных автоматов используются главным образом триггеры. Особенности построения цифровых устройств связаны со способом передачи информации между логическими элементами. Передача информации от элемента к элементу может осуществляться несинхронизируемым (асинхронным) и синхронизируемым способами, причем последний используется только при передаче информации в запоминающие элементы.
При несинхронизируемом способе передачи информации входные сигналы логических элементов преобразуются с небольшой задержкой в выходные сигналы, которые непосредственно воздействуют на входы следующих логических элементов.
При синхронизируемом способе передачи информации входные сигналы воздействуют на запоминающие логические элементы в строго определенные моменты времени, соответствующие появлению синхронизирующих сигналов.
Передача информации между запоминающими логическими элементами в общем случае требует выполнения следующего условия: она производится только после завершения передачи информации о предыдущем состоянии принимающего информацию элемента другому ЗЭ. Для выполнения этого условия в потенциальных схемах используется несколько серий синхронизирующих сигналов, сдвинутых во времени относительно друг друга так, что когда сигнал одной серии принимает значение 1, то сигнал другой серии — значение 0.