
Будем оценивать скорость тела по длине пути 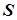 , пройденному телом по горизонтальной поверхности до полной остановки, считая коэффициент трения независящим от скорости скольжения. Пусть в некоторой точке скорость тела равна
, пройденному телом по горизонтальной поверхности до полной остановки, считая коэффициент трения независящим от скорости скольжения. Пусть в некоторой точке скорость тела равна  (рис. 3), тогда, по теореме об изменении кинетической энергии, работа силы трения равна изменению кинетической энергии тела
(рис. 3), тогда, по теореме об изменении кинетической энергии, работа силы трения равна изменению кинетической энергии тела
 ,
,  ,
,
откуда можно выразить скорость тела через расстояние  до точки остановки
до точки остановки
 .(6)
.(6)
Пусть перед соударением второе тело покоится, тогда для прямого центрального удара тел из формул (3) получаем
 ,
,  ,(7)
,(7)
где 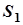 ,
,  – расстояния, проходимые телами 1 и 2 после соударения,
– расстояния, проходимые телами 1 и 2 после соударения,  – расстояние, которое прошло бы тело 1 до остановки без соударения с телом 2.
– расстояние, которое прошло бы тело 1 до остановки без соударения с телом 2.
Поскольку в эксперименте величины 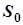 и
и  можно измерять с меньшей относительной погрешностью, то выразим коэффициент восстановления через них
можно измерять с меньшей относительной погрешностью, то выразим коэффициент восстановления через них
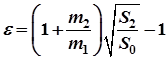 .(8)*
.(8)*
Коэффициент восстановления энергии (5) может быть рассчитан как
 .(9)*
.(9)*
Описание установки

Установка состоит из рабочего поля 3 (рис. 4) с нанесенной координатной сеткой, по которому перемещаются соударяющиеся тела 1 и 2. Начальную скорость телу 1 в направлении оси  сообщает ударный пружинный механизм 4. Перед выстрелом тело 1 фиксируется между направляющими 6. Регулировочный винт 5 позволяет изменять начальный импульс тела 1.
сообщает ударный пружинный механизм 4. Перед выстрелом тело 1 фиксируется между направляющими 6. Регулировочный винт 5 позволяет изменять начальный импульс тела 1.
Выполнение работы
Задание 1. Прямой центральный удар тел.
1. Выбрать два тела примерно равной массы. Значения масс  и
и  , а также систематическую погрешность взвешивания
, а также систематическую погрешность взвешивания  записать в таблицу 1.
записать в таблицу 1.

2. Поместить первое тело и второе тело на оси  так, чтобы поверхности 1 -го и 2 -го тела соприкасались (положение 1 -го тела отмечено на планшете окружностью). Начальные координаты тел (рис. 5) занести в таблицу. Оценить систематическую погрешность измерения координаты
так, чтобы поверхности 1 -го и 2 -го тела соприкасались (положение 1 -го тела отмечено на планшете окружностью). Начальные координаты тел (рис. 5) занести в таблицу. Оценить систематическую погрешность измерения координаты  .
.
3. Взвести пружинный механизм, зафиксировав его в первом пазу. Поместить шайбу 1 в направляющие. Произвести выстрел и занести в таблицу координаты крайних точек шайб  и
и  после соударения.
после соударения.
4. Поместить шайбу 2 в исходное положение.
5. Повторить опыт (п. 3 и п. 4) еще 6 раз при тех же условиях.
6. Определить скорость тела 1 при свободном движении. Для этого необходимо убрать с поля шайбу 2. Поместить в направляющие шайбу 1 и произвести выстрел. Записать в таблицу координату  точки остановки шайбы. Повторить опыт еще 5 раз, записывая результаты в таблицу.
точки остановки шайбы. Повторить опыт еще 5 раз, записывая результаты в таблицу.
Таблица 1
массы тел  : :
| 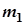 =, г =, г  =, г =, г  =, г =, г
| ||
| начальные координаты: |  =, мм =, мм  =, мм =, мм  =, мм =, мм
| ||
| после прямого удара | свободное движение | ||
| № |  , мм , мм
|  , мм , мм
|  , мм , мм
|
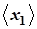 = =
|  = =
|  = =
| |
 = =
|  = =
| 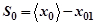 = =
|
7. Рассчитать средние значения конечных координат  ,
,  и
и  . Рассчитать средние расстояния, проходимые шайбами после удара
. Рассчитать средние расстояния, проходимые шайбами после удара  и
и  , а также среднюю длину пути свободного движения
, а также среднюю длину пути свободного движения  . Результаты занести в табл. 1.
. Результаты занести в табл. 1.
8. Вычислить значения коэффициентов и записать в табл. 2.
9. Оценить погрешность измерения величин. Поскольку систематическая погрешность измерения координаты в проводимых экспериментах намного меньше случайного отклонения от среднего значения, то ей можно пренебречь. Полагая, что измерения длин пробега проведены в одинаковых условиях, оценить погрешность определения этой величины только для случая свободного движения
 ,
,
где  – координаты точки остановки тела при свободном движении (см. табл. 1).
– координаты точки остановки тела при свободном движении (см. табл. 1).
Используя полученное значение, вычислить абсолютные погрешности коэффициентов восстановления и занести их в табл. 2.
Таблица 2
| величина | значения коэффициентов | погрешность |
| импульс |  = … = …
|  … …
|
| Кинетическая энергия |  = … = …
|  … …
|
| Относительная скорость |  = … = …
| – |
10. По средним значениям коэффициентов восстановления импульса, кинетической энергии и относительной скорости сделать вывод о справедливости законов сохранения импульса и энергии, для данного случая. Если коэффициент, характеризующий потери энергии отличен от нуля, то в выводе укажите основные причины изменения механической энергии рассматриваемой системы.
Задание 2. Косой центральный удар тел.
10. Взять для опыта шайбы, используемые при эксперименте с прямым ударом. Значения масс  и
и 
 записать в табл. 3.
записать в табл. 3.

11. Установить тела 1 и 2 в исходные положения, которые обозначены на поле окружностями. Записать начальные координаты крайних точек тел (см. рис. 6) в табл. 3.
12. Взвести пружинный механизм, зафиксировав его в первом пазу. Шайбу 1 вставить в направляющие до упора и произвести выстрел. Занести в таблицу 3 координаты крайних точек тел  ,
,  ,
,  ,
,  после остановки.
после остановки.
13. Поместить шайбу 2 в исходное положение с координатами  и
и  .
.
14. Повторяя действия пунктов 12 и 13, повторить опыт еще 6 раз.
15. Определить скорость тела 1 при свободном движении. Для этого необходимо убрать с поля шайбу 2. Поместить в направляющие шайбу 1 и произвести выстрел. Записать в таблицу координату  точки остановки шайбы. Повторить опыт еще 5 раз, записывая результаты в табл. 3.
точки остановки шайбы. Повторить опыт еще 5 раз, записывая результаты в табл. 3.
Таблица 3
 =, г =, г
|  =, г =, г
| ||||
 =,мм =,мм
| 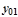 =,мм =,мм
|  =,мм =,мм
|  =,мм =,мм
| ||
| после удара | свободное движение | ||||
| № |  , мм , мм
|  , мм , мм
|  , мм , мм
|  , мм , мм
|  , мм , мм
|
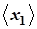 = =
|  = =
|  = =
|  = =
|  = =
|
Обработка результатов
16. Рассчитать средние значения конечных координат 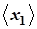 ,
,  ,
, 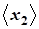 ,
,  и
и  . Вычислить средние расстояния, проходимые шайбами после удара
. Вычислить средние расстояния, проходимые шайбами после удара  и
и  , а также среднюю длину пути свободного движения
, а также среднюю длину пути свободного движения  по формулам
по формулам
 = … мм,
= … мм,
 = … мм,
= … мм,
 = … мм.
= … мм.
17. Вычислить значение коэффициента восстановления энергии при косом центральном ударе
 ,
, 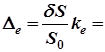
18. Сделать вывод по проделанной работе. По значениям коэффициентов восстановления классифицировать удар (упругий, неупругий). Высказать предположения о причинах диссипации энергии в конкретном случае. Объяснить различие (или равенство) экспериментальных значений коэффициента восстановления при прямом и косом центральном ударе.