Экономико-математические методы и модели в логистике
Предназначены для студентов экономического факультета НГАУ заочной формы обучения по направлению подготовки 38.03.02 Менеджмент профиль «Логистика и управление цепями поставок»
ЗАДАНИЯ КОНТРОЛЬНЫХ РАБОТ
Учебным планом по дисциплине «Математические методы и модели в логистике» предусмотрено выполнение двух контрольных работ. Ниже
приведены задания контрольной работы по каждой изучаемой теме и варианты контрольных заданий.
Номера выбираются согласно порядкового номера в журнале старосты
Тема 1. Прогнозирование
Задача 1. Известны данные динамического ряда оежемесячных доходах фирмы уt в тыс. руб. Выполнить экспоненциальное сглаживание динамического ряда с заданным параметром 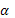 . По сглаженным значениям ряда, построить линейную регрессионную трендовую модель для прогнозирования, найдя её параметры. Изобразить графически в Excel исходные данные, их сглаженные значения и прямую регрессии. Сделать прогноз дохода на следующий месяц. Найти ошибку прогноза при заданном уровне надежности β; указать доверительный интервал прогноза; оценить относительную точность прогноза.
. По сглаженным значениям ряда, построить линейную регрессионную трендовую модель для прогнозирования, найдя её параметры. Изобразить графически в Excel исходные данные, их сглаженные значения и прямую регрессии. Сделать прогноз дохода на следующий месяц. Найти ошибку прогноза при заданном уровне надежности β; указать доверительный интервал прогноза; оценить относительную точность прогноза.
Варианты заданий:
№ 1. уt = (123; 125; 134; 138; 135; 125; 146; 139; 130; 140)  =0,28; β=0,95
=0,28; β=0,95
№ 2. уt = (112; 115; 124; 128; 125; 115; 136; 129; 120; 131)  =0,3; β=0,95
=0,3; β=0,95
№ 3. уt = (103; 105; 114; 118; 115; 105; 126; 119; 111; 120)  =0,28; β=0,9
=0,28; β=0,9
№ 4. уt = (10; 9; 12; 10; 11; 13; 15; 14) 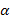 =0,5; β=0,9
=0,5; β=0,9
№ 5. уt = (151; 155; 164; 168; 165; 155; 176; 170; 163)  =0,25; β=0,95
=0,25; β=0,95
№ 6. уt = (82; 91; 102; 106; 101; 92; 115; 105; 98; 104)  =0,3; β=0,9
=0,3; β=0,9
№ 7. уt = (133; 135; 144; 148; 145; 135; 156; 149; 140)  =0,25; β=0,9
=0,25; β=0,9
№ 8. уt = (100; 102; 111; 115; 112; 102; 123; 116; 108; 118) 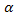 =0,26; β=0,95
=0,26; β=0,95
№ 9. уt = (136; 138; 147; 151; 148; 138; 159; 152; 143; 141)  =0,28; β=0,95
=0,28; β=0,95
№ 10. уt = (70; 83; 91; 95; 93; 82; 103; 96; 87; 94) 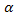 =0,32; β=0,9
=0,32; β=0,9
№ 11. уt = (68; 70; 79; 83; 81; 70; 91; 84; 75; 84) 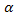 =0,28; β=0,9
=0,28; β=0,9
№ 12. уt = (200; 275; 252; 284; 241; 249; 276; 295; 260)  =0,4; β=0,9
=0,4; β=0,9
№ 13. уt = (125; 127; 136; 140; 137; 127; 148; 141; 132; 142)  =0,29; β=0,95
=0,29; β=0,95
№ 14. уt = (114; 117; 126; 130; 127; 117; 138; 129; 122; 133) 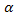 =0,33; β=0,9
=0,33; β=0,9
№ 15. уt = (105; 107; 116; 120; 117; 107; 128; 121; 113; 122)  =0,28; β=0,99
=0,28; β=0,99
№ 16. уt = (12; 11; 14; 12; 13; 15; 17; 16)  =0,5; β=0,9
=0,5; β=0,9
№ 17. уt = (153; 156; 166; 170; 167; 156; 178; 172; 165)  =0,25; β=0,95
=0,25; β=0,95
№ 18. уt = (84; 93; 104; 108; 103; 94; 117; 108; 100; 106)  =0,3; β=0,9
=0,3; β=0,9
№ 19. уt = (135; 137; 146; 150; 147; 135; 158; 151; 142)  =0,25; β=0,9
=0,25; β=0,9
№ 20. уt = (101; 103; 112; 116; 114; 104; 124; 117; 109; 110)  =0,26; β=0,95
=0,26; β=0,95
№ 21. уt = (138; 140; 149; 153; 150; 140; 161; 154; 146; 143)  =0,28; β=0,95
=0,28; β=0,95
№ 22. уt = (72; 85; 93; 97; 95; 84; 105; 98; 89; 96)  =0,32; β=0,9
=0,32; β=0,9
№ 23. уt = (70; 72; 81; 85; 83; 72; 93; 86; 77; 88)  =0,28; β=0,9
=0,28; β=0,9
№ 24. уt = (202; 277; 254; 286; 243; 251; 278; 297; 262)  =0,4; β=0,9
=0,4; β=0,9
№ 25. уt = (71; 84; 92; 96; 94; 83; 104; 97; 88; 95)  =0,3; β=0,95
=0,3; β=0,95
Задача 2. По квартальным данным динамического ряда об уровнях продаж 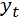 некоторого товара в тыс. рублей выделить аддитивную или мультипликативную сезонную компоненту и сделать прогноз продаж на следующие четыре квартала с учётом трендовой и сезонной составляющих. Оценить точность прогноза.
некоторого товара в тыс. рублей выделить аддитивную или мультипликативную сезонную компоненту и сделать прогноз продаж на следующие четыре квартала с учётом трендовой и сезонной составляющих. Оценить точность прогноза.
Варианты заданий:
№ 1. уt = (35; 38; 28; 30; 41; 44; 31; 35; 47; 49; 35; 39)
№ 2. уt = (15; 12; 13; 21; 20; 15; 18; 26; 25; 20; 23; 30)
№ 3. уt = (14; 25; 15; 12; 17; 28; 17; 13; 20; 31; 19; 18; 22)
№ 4. уt = (11; 22; 12; 9; 14; 23; 14; 10; 17; 28; 16; 15; 20)
№ 5. уt = (20; 32; 23; 20; 25; 34; 25; 21; 28; 39; 27; 25; 31)
№ 6. уt = (10; 7; 8; 16; 15; 11; 13; 21; 20; 15; 18; 25)
№ 7. уt = (12; 9; 10; 18; 17; 13; 15; 23; 22; 18; 20; 27)
№ 8. уt = (7; 6; 8; 18; 12; 12; 15; 23; 18; 17; 20; 27)
№ 9. уt = (24; 35; 25; 22; 27; 38; 27; 23; 30; 41; 29; 28; 32; 45)
№ 10. уt = (14; 25; 16; 12; 17; 28; 17; 13; 20; 31; 19; 18; 22; 35)
№ 11. уt = (13; 25; 24; 10; 17; 28; 27; 13; 20; 31; 29; 18; 22; 34)
№ 12. уt = (11; 24; 14; 10; 17; 28; 17; 12; 20; 31; 19; 16; 22; 34)
№ 13. уt = (36; 39; 29; 31; 42; 45; 32; 36; 48; 50; 36; 40)
№ 14. уt = (16; 13; 14; 22; 21; 16; 19; 27; 26; 21; 24; 29)
№ 15. уt = (14; 25; 15; 12; 17; 28; 17; 13; 20; 31; 19; 18; 22)
№ 16. уt = (12; 23; 13; 10; 15; 24; 15; 11; 18; 29; 17; 16; 21)
№ 17. уt = (19; 31; 22; 19; 24; 33; 24; 20; 27; 38; 26; 24; 30)
№ 18. уt = (11; 8; 9; 17; 16; 12; 14; 22; 21; 16; 19; 26)
№ 19. уt = (13; 10; 11; 19; 18; 14; 16; 24; 23; 19; 21; 28)
№ 20. уt = (8; 7; 9; 19; 13; 13; 16; 24; 19; 18; 21; 28)
№ 21. уt = (25; 36; 26; 23; 28; 39; 28; 24; 31; 42; 30; 29; 33; 46)
№ 22. уt = (15; 26; 17; 13; 18; 29; 18; 14; 21; 32; 20; 19; 23; 36)
№ 23. уt = (14; 26; 25; 11; 18; 29; 28; 14; 21; 32; 29; 18; 22; 35)
№ 24. уt = (12; 24; 16; 11; 17; 28; 18; 12; 20; 31; 20; 16; 20; 33)
№ 25. уt = (9; 8; 10; 20; 14; 13; 17; 25; 20; 19; 22; 29)
Тема 2. Системы массового обслуживания
Задача. Отгрузка производится со склада имеющего n погрузочных площадок. На склад для погрузки поступает простейший поток грузовиков с интенсивностью λ машин в час. Среднее время погрузки одной машины составляет tобсл минут. Если все погрузочные площадки заняты, то грузовики становятся в очередь.
Определить интенсивность обслуживания и параметр загрузки системы.
1) Сколько погрузочных площадок должен иметь склад, чтобы очередь не была бесконечной?
2) Назвать возможные состояния СМО и найти соответствующие им вероятности.
3) Найти вероятность того, что очереди нет.
4) Какова вероятность наличия очереди?
5) Какова вероятность, что в очереди более «k » грузовиков? Не более чем «k » грузовиков?
6) Найти среднее количество грузовиков в очереди.
7) Указать среднее время пребывания грузовика в очереди.
8) Каково среднее число грузовиков на складе?
9) Найти среднее время пребывания грузовика на складе.
Оценить работу склада с помощью найденных показателей эффективности.
| Варианты | λ | tобсл | n | k |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. | ||||
| 11. | ||||
| 12. | ||||
| 13. | ||||
| 14. | ||||
| 15. | ||||
| 16. | ||||
| 17. | ||||
| 18. | ||||
| 19. | ||||
| 20. | ||||
| 21. | ||||
| 22. | ||||
| 23. | ||||
| 24. | ||||
| 25. |
Тема 3. Управление запасами
Задача. Годовой спрос на товар составляет D едениц, стоимость подачи заказа С0 руб./ заказ, закупочная цена С руб./ ед., годовая стоимость хранения одной единицы товара составляет a % её цены. Время доставки заказа 6 дней, один год состоит из 300 рабочих дней. Найти: оптимальный размер заказа; минимальные годовые издержки на завоз и хранение одной партии товара; крличество поставок в год; интервал времени между двумя последовательными поставками; уровень повторного заказа.
Годовая стоимость отсутствия запасов составляет Сd руб./единица. Сравнить по уровню издержек две модели: основную и с дефицитом, если заявки выполняются.
Можно получить скидку b % у поставщика, если размер заказа будет не менее K единиц. Стоит ли воспользоваться скидкой?
Темп производства r ед./день. Найти экономичный размер партии; минимальные годовые издержки на завоз и хранение одной партии товара; кличество поставок в год; интервал времени между двумя последовательными поставками;время для пополнения запаса; максимальный товарный запас.
| Варианты заданий: | D | Со | С | a % | Сd | b % | K | r |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. | ||||||||
| 7. | ||||||||
| 8. | ||||||||
| 9. | ||||||||
| 10. | ||||||||
| 11. | ||||||||
| 12. | ||||||||
| 13. | ||||||||
| 14. | ||||||||
| 15. | ||||||||
| 16. | ||||||||
| 17. | ||||||||
| 18. | ||||||||
| 19. | ||||||||
| 20. | ||||||||
| 21. | ||||||||
| 22. | ||||||||
| 23. | ||||||||
| 24. | ||||||||
| 25. |