Разрывные колебания мультивибратора

С разрывными колебаниями»

Выполнили студенты 432 группы

Кононов Р.А.

Мишустов С.П.

Нижний Новгород

Цель работы: изучение динамики систем, совершающих разрывные колебания, на примерах мультивибратора, триггера и кипп-реле.

Приборы и оборудование: экспериментальная установка, включающая в себя схемы мультивибратора и кипп-реле; генератор сигналов AFG 3102; осциллограф GOS 620FG.

Система с нелинейностью «туннельный диод» и ее состояния равновесия.

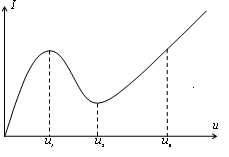
Схемы, динамика которых является предметом исследования, содержит в качестве нелинейного элемента туннельные диоды. Вольтамперная характеристика такого диода приведена на рисунке 1.

Рис. 1. Вольт-амперная характеристика туннельного диода

Характеристика имеет падающий участок (u₁<u<u₂), на котором проводимость туннельного диода является отрицательной величиной, что и позволяет получить разрывные колебания.

Схема, выполненная на туннельных диодах, приведена на рисунке 2, процессы в ней описываются следующими уравнениями:

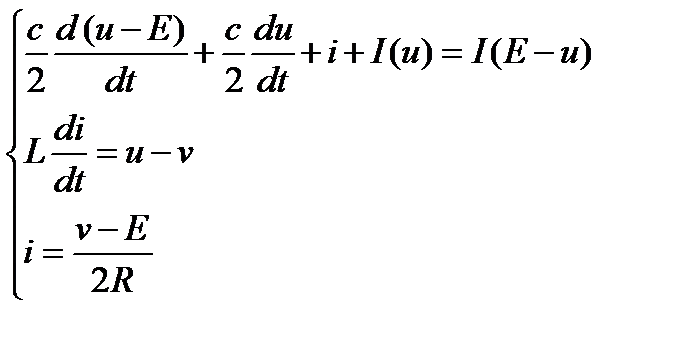
(1)

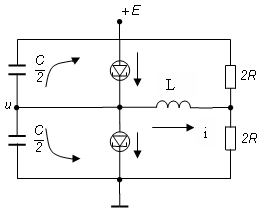
Рис. 2. Принципиальная схема мультивибратора

Если перейти к новым безразмерным переменным: ,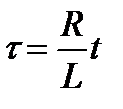

параметр 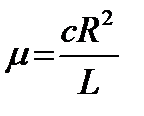, , 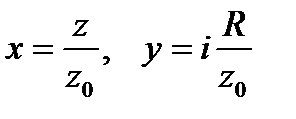, , 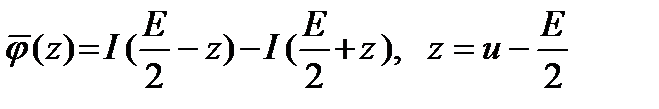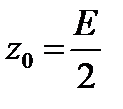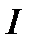- ток через туннельный диод, получим следующие уравнения:

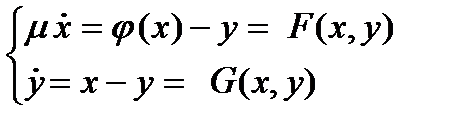
(2)

В системе, описываемой системой уравнений (2), возможны разрывные колебания, если 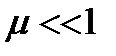. Это система с малым параметром при старшей производной.

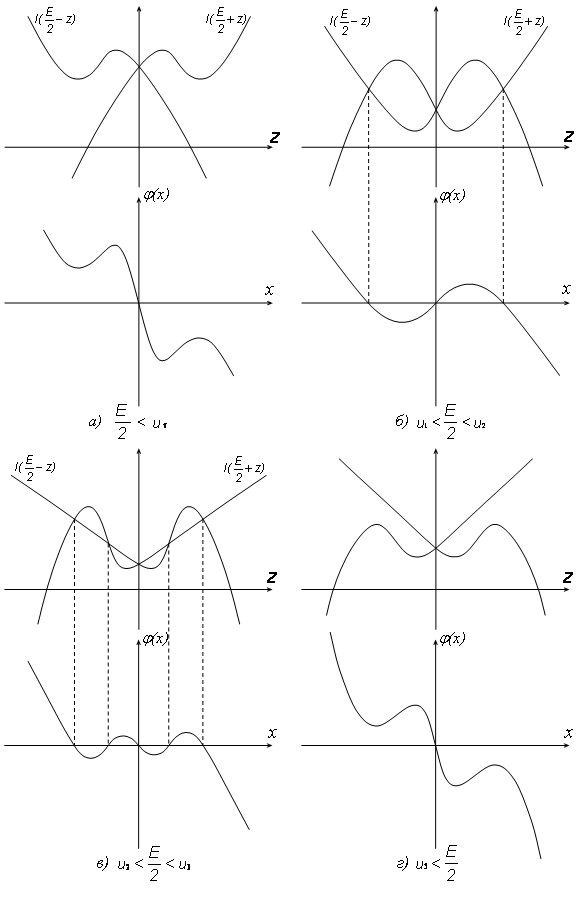
В зависимости от напряжения питания 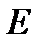функция φ(x) может принимать вид, изображенный на рисунке 3, при этом состояния равновесия системы (2 )

(x₀, y₀ ) определяются пересечением кривой 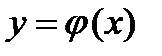с биссектрисой x=y. Таким образом, как видно из рисунка 3, схема может иметь от одного до пяти равновесных состояний.

Рис. 3. Возможные виды функции φ(x)

Разрывные колебания мультивибратора

Рассмотрим случай, когда φ(x) имеет вид, изображенный на рисунке 3(б), а состояние равновесия единственное. Это соответствует условию 0<S(0)<1 и тогда оно неустойчиво (с.р. будет всегда неустойчиво, т к ).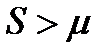

Система описывается уравнениями (2)

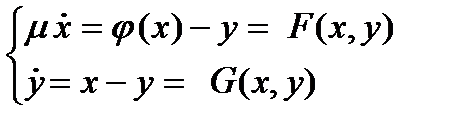
	(2)

Рассмотрим разбиения фазовой плоскости на траектории при 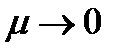(рис 4).

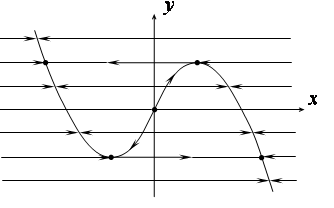
Рис. 4. Разбиения фазовой плоскости на траектории

Уравнения вида

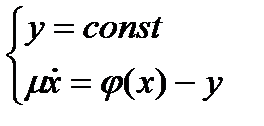
(3)

описывают так называемые «быстрые» движения системы. Направление движения определяется вторым уравнением. Эти приближенные (тем более точные, чем меньше 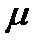) уравнения отображают динамику системы только вне малой окрестности кривой .

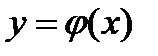Движения в малой окрестности кривой 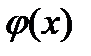, где 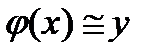, называются «медленными» движениями. Они отображаются следующими уравнениями:

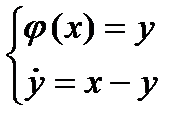
(4)

Кривая «медленных» движений определяется первым уравнением, а направление движения на участках «медленных» движений - из второго уравнения системы (4).

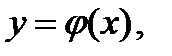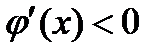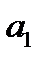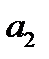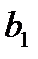
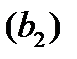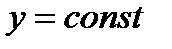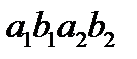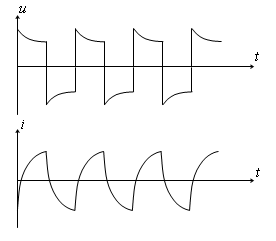
Если изображающая точка системы, «медленно» двигаясь по траектории там, где , (а только здесь медленные движения устойчивы) приходит в одну из точек или , то далее она выходит в область «быстрых» движений и скачком попадает в точку по траектории , пока снова не придет на траекторию «медленного» движения. Замкнутая кривая является предельным циклом, устанавливающимся при любых начальных условиях. Такая система является автоколебательной, генерирующей разрывные колебания. Осциллограммы колебаний u и i приведены на рисунке 5.

Рис.5. Осциллограммы разрывных колебаний