Тема урока — Арифметические операции в позиционных системах счисления

Урок посвящен теме «Арифметические операции в позиционных системах счисления»».

В ходе урока школьники научатся складывать, вычитать, умножать и делить в разных позиционных системах счисления.

Ключевые слова:

— позиционные системы счисления,

— арифметические операции в системе счисления с основанием q,

— таблица сложения,

— таблица умножения.

Учебник:

— Информатика. 10 класс: учебник / Л. Л. Босова, А. Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2016. - 288 с.

— Математические основы информатики: учебное пособие / Е. В. Андреева, Л. Л Босова, И. Н. Фалина — М.: БИНОМ. Лаборатория знаний, 2008. - 328 с.

Мы продолжаем изучать позиционные системы счисления. Вы узнали, что позиционные системы счисления бывают разные: десятичная, двоичная, восьмеричная и шестнадцатеричная. Вы научились переводить числа из одной системы счисления в другую. Но зачем нам с вами это надо? Конечно для того, чтобы производить расчеты. С 1 класса нас учат производить расчеты в десятичной системе счисления. А как вы думаете, можно ли производить расчеты в произвольной позиционной системе счисления? И зачем это нужно?

Двоичная система счисления издавна была предметом пристального внимания многих ученых. Первый кто заговорил о двоичном кодировании, был Лейбниц Готфрид Вильгельм. Он написал трактат «Expication de l'Arithmetique Binary» — об использовании двоичной системы счисления в вычислительных машинах. В рукописи на латинском языке, написанной в марте 1679 года, Лейбниц разъясняет, как выполнять вычисление в двоичной системе, в частности умножение, а позже в общих чертах разрабатывает проект вычислительной машины, работающей в двоичной системе счисления. Вот что он пишет: «Вычисления такого рода можно было бы выполнять и на машине». Эти слова подчеркивают универсальность алфавита, состоящего из двух символов.

Все позиционные системы счисления “одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

— справедливы одни и те же законы арифметики: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный);

— справедливы правила сложения, вычитания, умножения и деления столбиком.

Мы узнаем на уроке:

1. как строить таблицы сложения и умножения в заданной позиционной системе счисления;

2. как выполнять сложение, умножение, вычитание и деление чисел, записанных в двоичной, восьмеричной и шестнадцатеричной системах счисления;

3. как подсчитывать количество единиц в двоичной записи числа, являющегося результатом суммирования или вычитания степеней двойки.

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

Рассмотрим сложение.

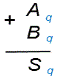
Чтобы в системе счисления с основанием q получить сумму S двух чисел A и B, надо просуммировать образующие их цифры по разрядам i справа налево:

1. если a_i + b_i < q, то s_i = a_i + b_i,
старший (i + 1)-й разряд не изменяется

2. если a_i + b_i ≥ q, то s_i = a_i + b_i – q,
старший (i + 1)-й разряд увеличивается на 1

Можно составить таблицу сложения:

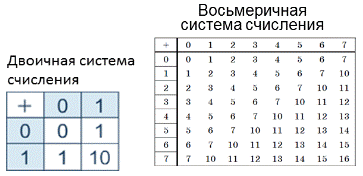
Давайте рассмотрим правило сложения на примере в двоичной системе счисления

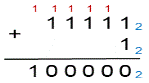
Это мы рассмотрели сложение в двоичной системе счисления, а теперь сложим два числа в троичной, восьмеричной и шестнадцатеричной системе счисления.

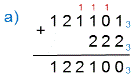
— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 2-м разрядом,
а 3-й разряд увеличиваем на 1

— 1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1

— 1 + 1 = 2 < 3
записываем 2 под 4-м разрядом

Сложим в восьмеричной и шестнадцатеричной системе счисления.

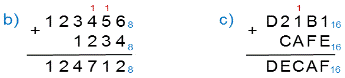
Теперь разберём вычитание в системах счисления с основанием q.

Чтобы в системе счисления с основанием q получить разность R двух чисел A и B, надо вычислить разности образующих их цифр по разрядам i справа налево:

— если a_i ≥ b_i, то r_i = a_i – b_i,
старший (i + 1)-й разряд не изменяется

— если a _i < b _i , то r_i = q + a_i – b_i ,

старший (i + 1)-й разряд уменьшается на 1

Рассмотрим правило вычитания в двоичной системе счисления на примере.

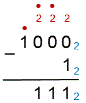
Рассмотрим правило вычитания в троичной системе счисления, где q=3

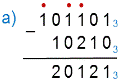
1. 1 ≥ 0
записываем 1 – 0 = 1 под 1-м разрядом

2. 0 < 1
записываем 3 + 0 – 1 = 2 под 2-м разрядом,
делая заем в 3-м разряде

3. 0 < 2
записываем 3 + 0 – 2 = 1 под 3-м разрядом,
делая заем в 4-м разряде

4. 0 = 0
записываем 0 под 4-м разрядом

5. 0 < 1
записываем 3 + 0 – 1 = 2 под 5-м разрядом,
делая заем в 6-м разряде

В восьмеричной и шестнадцатеричной системе выполним вычитание.

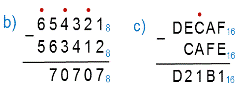
Как же выполняется умножение чисел в системе счисления с основанием q? Если мы рассмотрим таблицы умножения в двоичной, троичной, восьмеричной и шестнадцатеричной системах счисления, то увидим, что алгоритм умножения точно такой же, как и в десятичной системе.

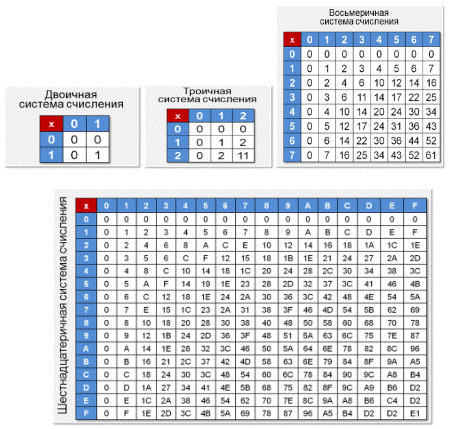
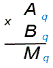
Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i:

1. если a_i · b <q, то m_i = a_i · b,
старший (i + 1)-й разряд не изменяется

2. если a_i · b ≥ q, то m_i = a_i · b mod q,
старший (i + 1)-й разряд увеличивается на a_i · b div q

Рассмотрим примеры:

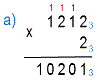
— 2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1

— 1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1

— 2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1

— 2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1

По этому алгоритму выполним умножение в других системах счисления.

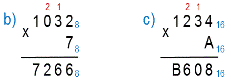
Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Посмотрим пример в двоичной системе счисления.

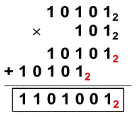
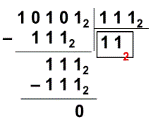
Деление нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления. А значит, нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q. Давайте разберем деление в двоичной системе.

И попробуем поделить в восьмеричной системе счисления.

В числе 233₈ поместится 2 ∙ 73₈ = 166₈

В числе 456₈ поместится 5 ∙ 73₈ = 447₈

В числе 73₈ поместится 1 ∙ 73₈ = 73₈

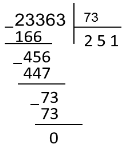
Теперь мы знаем, как производится арифметика в двоичной системе счисления. Используя таблицы, мы можем решить любой пример.

Давайте рассмотрим пример:

Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6

Решение:

Представим все операнды исходного выражения в виде степеней двойки:

Исходное выражение 2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6

примет вид 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹

Перепишем выражение в порядке убывания степеней: 2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1; 2² = 100 = 11 + 1; 2³ = 1000 = 111 + 1; …

В общем виде

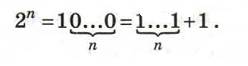
Для натуральных n и m таких, что n > m, получаем:

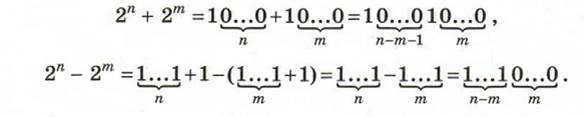
Эти соотношения позволят подсчитать количество «1» в выражении без вычислений. Двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной «1». Разность 2²⁰¹⁸ – 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2² и 2¹ дают ещё 2 единицы.

Так как в задаче надо найти единицы, то получаем:

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Давайте разберем еще одну задачу.

Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения: 2²⁹⁹ + 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

Решение:

Двоичное представление исходного числа имеет вид:

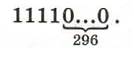
Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Ответ: 100 цифр

Итак, сегодня вы узнали, что арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления. Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно:

1. все операнды представить в привычной нам десятичной системе счисления;

2. вычислить результат выражения в десятичной системе счисления;

3. перевести результат в требуемую систему счисления.

Для работы с десятичными числами вида 2ⁿ, полезно иметь ввиду следующие закономерности в их двоичной записи:

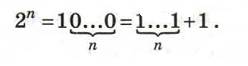
Для натуральных n и m таких, что n > m, получаем:

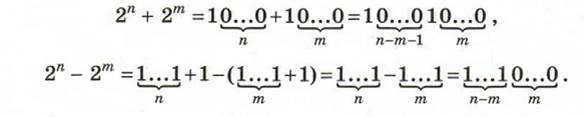
Тренировочный модуль.

1 задание

Выберите выражения, значения которых одинаковые.

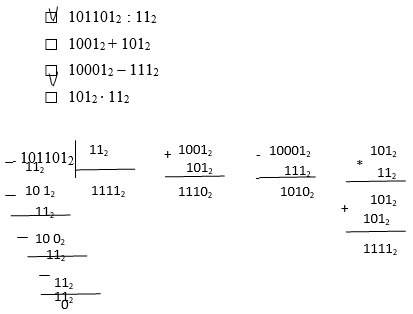
Возьми карандаш и подчеркни результат сложения

14₅ + 32₅

22₅ 103₅ 43₅ 101₅

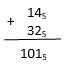
Реши кросснамбер

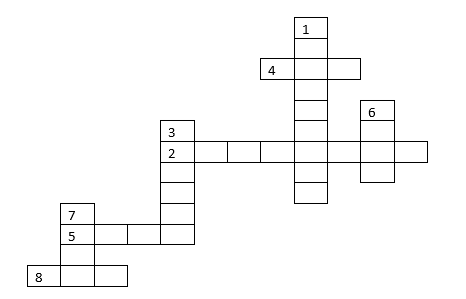
По вертикали:

1. Найди сумму и запиши в двоичной системе счисления 153₈ + F9₁₆

3. Найди произведение и запиши в двоичной системе счисления 122₃ * 11₂

6. Выполни операцию деления 10010000₂ / 1100₂

7. Реши пример, ответ запиши в десятичной системе счисления (564₈ + 234₈) * C₁₆

По горизонтали:

2. Разность двоичных чисел 11001100 - 11111

4. Найти разность 167₈ – 56₈

5. Выполнить операцию деления 41612₈ / 12₈

8. Найти разность 12E₁₆ – 79₁₆ ответ запиши в десятичной системе счисления