Постановка задачи 5.5. Разработать алгоритм и программу для решения нелинейного уравнения с параметрами методом половинного деления. С помощью программы вычислить все корни уравнений в соответствии с указанным вариантом и заданной точностью 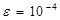 . Параметр a задать самостоятельно методом перебора. Определить для каких a уравнение имеет 1,2,3,4,5 действительных корней.
. Параметр a задать самостоятельно методом перебора. Определить для каких a уравнение имеет 1,2,3,4,5 действительных корней.
Таблица.5.5.1
Варианты уравнений
| номер варианта | Уравнение |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |
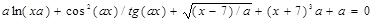
|
Окончание таблицы.5.5.1
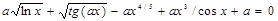
| |

| |

| |

| |

| |
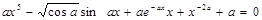
| |

| |

| |

| |
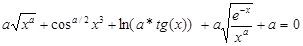
| |

| |

| |
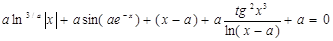
|
Для отчета по заданию необходимо представить: 1) постановку задачи; 2) алгоритм; 3) программу; 4) результаты решения, включающие таблицы решения уравнения F(x,a)=0 в зависимости от параметра a.
| параметр a | корни уравнения F(x,a)=0 | число корней уравнения |

| 
| |

| 
| |

| 
| |

| 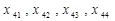
| |

| 
|
Эта таблица должна иллюстрировать количество корней уравнения для F(x,а)=0 (ограничиться 5-тью корнями при заданном). Построить график функции F(x,a) от x для параметра a соответствующего наибольшему количеству корней найденных в задании. Если заданное (5) число корней не удалось найти, то следует объяснить “почему”.
Задача 5.6. Аппроксимация табулированных функций по методу наименьших квадратов
Постановка задачи 5.6. Разработать алгоритм и программу для выбора аппроксимирующего многочлена вида  для табулированной функции y=f(x). Исходные данные для построения многочлена представлены в таблицах. 5.5.2 и 5.5.3(варианты заданий).
для табулированной функции y=f(x). Исходные данные для построения многочлена представлены в таблицах. 5.5.2 и 5.5.3(варианты заданий).
Таблица 5.5.2
Значения переменных  для построения многочлена y=f(x)
для построения многочлена y=f(x) 
| n | 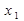
| 
| 
| 
| 
| 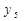
| 
|
| 0,1 | 2,57 | 0,15 | 2,98 | 3,19 | 6,54 | 7,26 | |
| 0,3 | 3,87 | -0,01 | 3,45 | 1,59 | 6,63 | 7,95 | |
| 0,5 | 5,67 | 0,46 | 3,84 | 0,4 | 6,83 | 8,77 | |
| 0,7 | 8,39 | 1,71 | 3,87 | 0,22 | 7,34 | 9,72 | |
| 0,9 | 12,9 | 3,94 | 3,24 | 1,95 | 8,44 | 10,78 | |
| 1,1 | 20,47 | 7,4 | 1,73 | 6,84 | 10,48 | 12,45 | |
| 1,3 | 32,84 | 12,41 | -0,67 | 16,58 | 13,71 | 14,74 | |
| 1,5 | 52,17 | 19,47 | -3,78 | 33,4 | 18,7 | 18,18 | |
| 1,7 | 81,1 | 29,21 | -7,07 | 60,08 | 25,87 | 23,36 | |
| 1,9 | 122,68 | 42,49 | -9,62 | 100,1 | 35,76 | 30,99 | |
| 2,1 | 180,44 | 60,43 | -10,04 | 157,67 | 48,93 | 41,97 | |
| 2,3 | 268,38 | 84,42 | -6,39 | 237,83 | 65,97 | 57,38 | |
| 2,5 | 360,93 | 116,18 | 3,89 | 346,5 | 87,52 | 78,45 | |
| 2,7 | 493,01 | 157,8 | 24,08 | 490,6 | 114,23 | 106,65 | |
| 2,9 | 211,78 | 58,21 | 678,09 | 146,8 | 143,64 | ||
| 3,1 | 867,76 | 281,04 | 111,19 | 918,06 | 185,93 | 191,28 | |
| 3,3 | 1122,64 | 188,86 | 1220,08 | 232,35 | 251,71 |
Окончание таблицы 5.5.2
| 3,5 | 1431,43 | 479,59 | 298,07 | 1597,9 | 286,78 | 327,27 | |
| 3,7 | 1801,46 | 617,3 | 446,74 | 2062,29 | 349,99 | 420,58 | |
| 3,9 | 2240,52 | 787,21 | 643,99 | 2628,34 | 422,73 | 534,52 | |
| 4,1 | 2756,88 | 995,04 | 900,13 | 3311,95 | 505,74 | 672,24 | |
| 4,3 | 3359,35 | 1247,17 | 1226,83 | 4130,59 | 599,78 | 837,2 | |
| 4,5 | 4057,19 | 1550,71 | 1637,14 | 5103,4 | 705,6 | 1033,14 | |
| 4,7 | 4860,21 | 1913,5 | 2145,58 | 6251,27 | 823,94 | 1264,13 | |
| 4,9 | 5778,7 | 2344,18 | 2768,2 | 7596,91 | 955,52 | 1534,54 | |
| 5,1 | 6823,5 | 2852,21 | 3532,71 | 9164,91 | 1101,05 | 1849,11 | |
| 5,3 | 8005,85 | 3447,91 | 4428,49 | 10980,87 | 1261,21 | 2212,91 | |
| 5,5 | 9337,7 | 4142,52 | 5506,72 | 13076,4 | 1436,67 | 2631,36 | |
| 5,7 | 10831,38 | 4948,19 | 6780,41 | 15479,26 | 1628,06 | 3110,26 | |
| 5,9 | 12499,79 | 5878,09 | 8274,53 | 18223,42 | 1835,97 | 3665,8 | |
| 6,1 | 14356,37 | 6946,36 | 10016,04 | 21344,1 | 2060,97 | 4274,55 | |
| 6,3 | 16415,09 | 8768,24 | 12033,99 | 24878,92 | 2303,59 | 4973,5 | |
| 6,5 | 18690,45 | 9560,03 | 14359,59 | 28867,9 | 2564,29 | 5760,63 | |
| 6,7 | 21197,51 | 11139,19 | 17026,29 | 33353,59 | 2843,52 | 6641,98 | |
| 6,9 | 23951,86 | 12924,34 | 20069,86 | 38381,12 | 3141,65 | 7627,6 | |
| 7,1 | 26969,66 | 14935,29 | 23528,45 | 43998,25 | 8725,62 | ||
| 7,3 | 30267,6 | 17193,14 | 27442,7 | 50255,62 | 3795,83 | 9945,22 | |
| 7,5 | 33862,96 | 19720,24 | 31855,77 | 57806,5 | 4152,36 | 11296,05 | |
| 7,7 | 37773,55 | 22540,29 | 36813,46 | 64907,16 | 4528,7 | 12788,24 | |
| 7,9 | 42017,77 | 25678,32 | 42364,27 | 73416,84 | 4924,93 | 14432,44 |
Таблица 5.5.3
Варианты заданий
| номер | Вид функции | степень многочлена |

| 3,5,7 | |
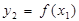
| 2,4,6 | |

| 2,3,4 | |

| 3,4,7 | |

| 3,4,6 | |
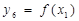
| 2,3,5 | |

| 2,7,8 | |

| 3,5,6 | |
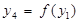
| 3,7,8 | |

| 2,5,6 | |
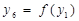
| 3,4,5 | |
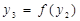
| 3,4,7 | |

| 3,6,7 | |

| 2,3,6 | |
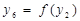
| 2,4,5 | |

| 3,4,6 | |

| 3,5,7 | |

| 2,4,6 | |

| 2,3,4 | |

| 3,4,7 | |

| 3,5,7 | |

| 2,4,6 |
Окончание табл. 5.5.3

| 2,3,4 | |
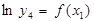
| 3,4,7 | |
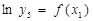
| 2,3,4 | |

| 3,4,7 |
При построении многочлена для функции 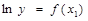 необходимо данные
необходимо данные 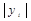 линеаризовать, прологарифмировав данные столбца. Вся дальнейшая методика построения многочлена аналогична вариантам 1-20.
линеаризовать, прологарифмировав данные столбца. Вся дальнейшая методика построения многочлена аналогична вариантам 1-20.
При разработке алгоритма и программы можно пользоваться программой для решения системы линейных уравнений (раздел 4.1.). При этом каждый студент решает свою систему линейных уравнений, которую необходимо составить на основе данных табл. 5.5. и 5.6.. Например, для расчета коэффициентов полинома 6 степени  необходимо решить систему уравнений вида:
необходимо решить систему уравнений вида:

где  ,
,  ,
,  ,
,  ,
, 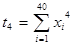 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Результаты решения задачи должны включать найденные коэффициенты полиномов  и построение графика
и построение графика  вместе с исходными данными. Для 3-х различных полиномов (степень полинома, табл. 6.6.) рассчитать среднеквадратичное отклонение
вместе с исходными данными. Для 3-х различных полиномов (степень полинома, табл. 6.6.) рассчитать среднеквадратичное отклонение
 , где
, где  -табулированное значение, y(x)-аппроксимированный многочлен, по которому нужно оценить близость полинома к исходным данным (табл.5.6.) Сделать выводы об лучшей аппроксимации.
-табулированное значение, y(x)-аппроксимированный многочлен, по которому нужно оценить близость полинома к исходным данным (табл.5.6.) Сделать выводы об лучшей аппроксимации.
Таким образом, студент, выполняющий 4 вариант должен построить три полинома вида:

и вычислить среднеквадратическое отклонение для каждого полинома.