Задачи для самостоятельного решения. Проведем KM||AB. По теореме Фалеса СМ=МВ

Решение

 

Проведем KM || AB. По теореме Фалеса СМ = МВ. Проведем LM || BB ₁, L – середина С ₁ В ₁. По 2.9 (Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны) получим (KML)||(AA ₁ B ₁) Þ KL ||(AA ₁ B ₁). Пусть АВ = а, АА ₁ = b. Тогда

Ответ: .

 

 

Таблица 3

 

Геометрический объект	Угол между пересекающимися прямыми	Угол между скрещивающимися прямыми
Определение	3.1.Величина угла между пересекающимися прямыми (a) и (b) равна величине вертикальных не тупых углов, образованных этими прямым). .	3.6 Угол между скрещивающимися прямыми (b и a) равен углу между параллельными им пересекающимися прямыми (b и c)
Изображение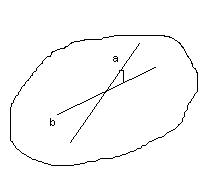
Свойства	3.2*.Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые. 3.3.Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая перпендикулярна третьей прямой.	3.7*. Угол между скрещивающимися прямыми равен разности 90º и угла между плоскостью, перпендикулярной к одной из прямых и второй прямой.
Примечания	3.4*.Две прямые называются перпендикулярными, если угол между ним и равен 90º. 3.6. Угол между прямыми изменяется от 0º до 90º.	3.8** Угол между двумя скрещивающимися ребрами правильной треугольной пирамиды равен 90º.

Задачи

 

1.В правильном тетраэдре ABCD определите угол между прямой AD и прямой, содержащей медиану CM треугольника ACB.

Решение

Медиана CM треугольника ACB и ребро AD тетраэдра ABCD лежат на скрещивающихся прямых. В плоскости ADB проведем через точку M прямую, параллельную AD до пересечения с ребром DB в точке K. Тогда угол между прямой AD и прямой, содержащей медиану CM треугольника ACB (3.5) равен углу CMK.

Отрезок MK – средняя линия треугольника BDA. Тогда KM= 0,5a, где a- ребро тетраэдра.CK=CM=a .

В равнобедренном треугольнике CKM, СH – высота, тогда cos CMK = MH:CM= < CMK = arccos

Ответ: arccos

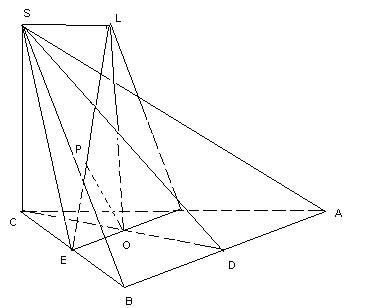
2.В основании пирамиды SABC лежит равносторонний треугольник ABC, длина стороны которого 4√2 см.Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. Найдите угол между прямыми SE и СD, где точки E и D– середины ребер BC и AB соответственно.

 

Решение

Построим плоскость, проходящую через точку E, перпендикулярную прямой CD. Это плоскость ELO, проходящая через две прямые LO и EO, перпендикулярные прямой CD. Прямая LE – проекция прямой SE на плоскость ELO. Искомый угол равен 90º - <SEL (3.7), LO = √6. CO = √6. tg(90º - <SEL) = ctg (<SEL) = 1, тогда <SEL= 45º.

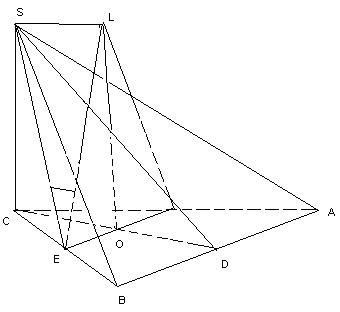
Ответ: 45º.

 

 

Таблица 4

 

Геометрический объект	Угол между прямой и плоскостью	Угол между плоскостями
Определение	4.1.Углом (φ) между прямой (AB) и плоскостью (α), не перпендикулярной данной плоскости, называется угол между прямой и ее проекцией (BC) на данную плоскость.   .	4.3.Двугранным углом (αaβ) называется фигура, образованная двумя полуплоскостями (αβ), с общей границей(a), не принадлежащими одной плоскости. Плоскости (α и β), образующие двугранный угол, называются гранями двугранного угла. Общая граница двух полуплоскостей(a) называется ребром двугранного угла. 4.4. Линейным углом (BAC) двугранного угла (αaβ) называется угол, образованный лучами(AB и AC) с общим началом(A) на ребре (a) двугранного угла, проведенными перпендикулярно ребру(AB a, AC a) в каждой грани (AB в грани α, AC в грани β). 4.5. Углом между пересекающимися плоскостями называется величина наименьшего из двугранных углов, образованных этими плоскостями.
Изображение
Свойства	4.2Угол между прямой и плоскостью - наименьший из всех углов, образованных данной прямой с прямыми, лежащими в плоскости	4. 6*.Угол между двумя пересекающимися плоскостями равен углу между прямыми, перпендикулярами к этим плоскостям.
Примечания	4.7**.Угол между прямой и плоскостью равен 90 º - α, где α- угол между прямой и перпендикуляром к даной плоскости.

 

Задачи

1. В кубе ABCDA₁B₁C₁D₁ найдите угол между диагональю DB₁ и плоскостью ABC.

 

Решение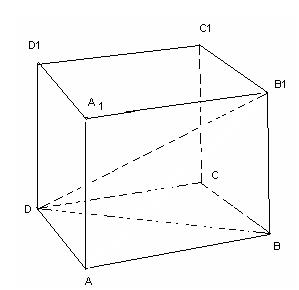

 

В кубе ABCDA₁B₁C₁D₁ угол между прямой DB₁и плоскостью ABC – это угол между проекцией этой прямой на плоскость ABC, т.е. прямой DB, и данной прямой прямой (4.1), т.е. это угол B₁DB. Обозначим длину ребра куба через a. Тогда диагональ куба BD равна a . Из прямоугольного треугольника ABC найдем тангенс угла B₁DB,

tg< B₁DB = a:a = ;< B₁DB= arctg .

 

Ответ: arctg

 

2.В правильном тетраэдре ABCD определите угол между гранями ABC и ABD

 

Решение

На рисунке в правильном тетраэдре ABCD построен линейный угол двугранного угла с ребром AB (4.5). В грани ABC DM AB в грани ABD CM AB. Тогда величина угла между гранями ABC и ABD равна величине линейного угла DMC.

Этот угол найдем из треугольника DMC по теореме косинусов.

Обозначим ребро тетраэдра ABCD через a. Тогда CM= DM=a ,

a² = 3/4 a²+ 3/4 a² - 2∙3/4 a²cos DMC, откуда cos DMC= 1/3, DMC= arccos 1/3

 

Ответ: угол между гранями ABC и ABD равен arccos 1/3.

 

 

Таблица 5

 

Геометрический объект	5.1. Перпендикулярные прямая и плоскость	Перпендикулярные плоскости
Определение	5.2.Прямая называется перпендикулярной плоскости, если прямая перпендикулярна каждой прямой, лежащей в плоскости.	5.9.Две плоскости называются взаимно перпендикулярными, если угол между ними равен 90º.
Изображение
Свойства	5.3.Признак перпендикулярности прямой и плоскости.Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. 5.3.Через любую точку пространства проходит плоскость, перпендикулярная данной прямой, и притом только одна.   5.4.Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то: а) перпендикуляр короче наклонных; б) равные наклонные имеют равные проекции; в) из двух наклонных та больше, проекция которой больше. 5.5. Если одна из двух параллельных прямых перпендикулярна плоскости, то и вторая прямая перпендикулярна этой плоскости 5.6. Если две прямые перпендикулярны одной плоскости, то эти прямые параллельны.   5.7.Теорема о трех перпендикулярах. Если прямая, лежащая в плоскости, перпендикулярна проекции некоторой наклонной к плоскости, то она перпендикулярна и самой наклонной. 5.8. Если прямая, лежащая в плоскости, перпендикулярна наклонной к плоскости, то она перпендикулярна и проекции наклонной на эту плоскость. .	5.10. Признак перпендикулярности плоскостей Если плоскость проходит через перпендикуляр к другой плоскости, то такие две плоскости будут перпендикулярны. 5.11.Если две плоскости перпендикулярны и в одной из них, проведена прямая, перпендикулярная к их линии пересечения, то эта прямая перпендикулярна второй плоскости. 5.12.Если две пересекающиеся плоскости перпендикулярны третьей, то линия их пересечения перпендикулярна третьей плоскости 5.13.*Если две плоскости перпендикулярны, то квадрат расстояния между двумя точками, принадлежащими разным плоскостям, равен сумме квадратов трех расстояний: расстояний от этих точек до линии пересечения плоскостей и расстояния между проекциями этих точек на линию пересечения плоскостей.
Примечания	5.14** Каждая диагональ куба перпендикулярна плоскости, проходящей через концы трех его ребер,выходящих из одной вершины куба, не принадлежащих этой диагонали.	5.15*.Каждые два диагональных сечения куба перпендикулярны.

 

Задачи

 

1. Отрезок AB не пересекает плоскость α. Расстояние от концов отрезка AB до плоскости α равны соответственно 6 и 10 см. Найдите расстояние от середины отрезка AB до плоскости α.

Решение

На рисунке отрезки AC и BD перпендикулярны плоскости α. AC=10см,

BD= 6 см. Так как прямые AC и BD перпендикулярны плоскости α.,то

AC ׀׀ BD (5.6). Проведем через AC и BD плоскость β, которая пересекает плоскость α по прямой CD.Тогда четырехугольник ACDB – трапеция. Проведем среднюю линию трапеции MN, по свойству средней линии она параллельна основаниям трапеции, а по теореме б) отрезок MN перпендикулярен плоскости α, значит, MN-искомый отрезок. Его длина равна полусумме длин отрезков AC и BD, как длина средней линии трапеции MN = 8см.

 

Ответ: 8см

2. Из точки A к плоскости α проведены перпендикуляр AB и наклонные AC и AD равной длины, проекции которых образуют между собой прямой угол. Найдите длины наклонных AC и AD, если расстояние CD=2cм, AB= 4см.

 

Решение

На рисунке треугольник CBD равнобедренный, так как отрезки CB и BD – проекции равных наклонных AC и AD

(5. 4). По условию треугольник CBD прямоугольный. Тогда CB =CD sin45º= (cм).

Из прямоугольного треугольника ABC найдем гипотенузу по катетам AB и BC. AC = (cм).

 

Ответ: 3√2 см.

 

3. Правильный шестиугольник ABCDEF со стороной 1 согнули по диагонали AD так, что его части оказались в перпендикулярных плоскостях. Вычислите новое расстояние между B и F, между отрезком AB и E.

 

Решение: По свойству 5.11, перпендикуляр BK к прямой AD перпендикулярен к плоскости AFE, а перпендикуляр FK к прямой AD перпендикулярен к плоскости ABC/ Поэтому D BKF – прямоугольный (рис.1)

. .

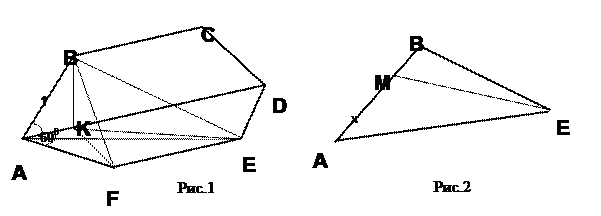
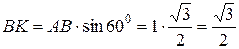BK = KF;

D ABE: ;

.

Пусть AM- перпендикуляр к прямой AB, AM = х Þ

 

 

Таким образом, расстояние между отрезком АВ и E равно , а новое расстояние между B и F равно .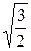

Ответ: , .

 

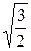4.Пусть ABC и ACD – два прямоугольных треугольника с катетами 3 и 4. Они имеют общую гипотенузу АС и лежат в перпендикулярных плоскостях. Вычислите расстояние BD (Возможны два случая).

 

Решение:

а) 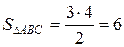(рис.1). ;

 

 

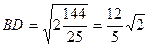
б) 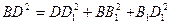(5.13) (рис.2)

▄

 

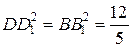
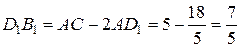
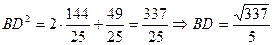Ответ: , .

 

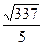Таблица 6

Геометрический объект	Расстояние между фигурами	Ортогональное проектирование
Определение	6.1. Расстоянием от точки A до некоторой фигуры называется расстояние от этой точки до ближайшей к ней точки фигуры.	6.8. Если направление параллельного проектирования таково, что прямая l перпендикулярна плоскости α, то такое проектирование называется ортогональным. Ортогональное проектирование – частный случай параллельного проектирования, поэтому обладает всеми его свойствами.
Изображение	Расстояние от AC – наименьшее из AB, AE, AD и т.д.
Свойства	6.2.Расстояние от точки A до прямой a равно длине перпендикуляра, проведенного из точки A к прямой a. 6.3.Расстояние от точки A до плоскости α равно длине перпендикуляра AB, проведенного из точки A к плоскости a 6.4.Расстоянием между параллельными прямыми равно расстоянию MN от какой- либо точки одной прямой до другой прямой. 6.5. Расстоянием между пересекающимися прямыми равно нулю. 6.6*а) Расстояние между скрещивающимися прямыми равно расстоянию от одной прямой до плоскости, содержащей вторую прямую и параллельную первой. б) Расстояние между скрещивающимися прямыми, одна из которых перпендикулярна некоторой плоскости, равно расстоянию от точки пересечения этой прямой с плоскостью до проекции второй прямой на эту плоскость. 6.7.Расстояние между параллельными плоскостями равно расстоянию от какой- либо точки одной плоскости до другой плоскости.	6.9.*Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостями многоугольника и его проекции. 6.10 Общим перпендикуляром двух скрещивающихся прямых называется отрезок, перпендикулярный каждой из этих прямых, с концами на данных прямых.
Примечание	6.11**. Расстояние между двумя параллельными сечениями куба, являющимися треугольниками с вершинами - в вершинах куба (например,A1DB и D1 C B1 ) равно a√3/3.	6.12**Расстояние между прямыми, содержащими скрещивающиеся диагонали смежных граней куба, равно a√3/3. 6.13**Расстояние между скрещивающимися ребрами правильного тетраэдра равно a√2/2.

 

Задачи

1. Площадь ортогональной проекции многоугольника ABCDEF на некоторую плоскость равна 12 см² , площадь многоугольника ABCDEF равна 24см². Найдите угол между плоскостями проекций и многоугольника.

Решение

По свойству 6.9 cos <α = 12/24 = ½, поэтому угол между плоскостями проекций и многоугольника равен

60°.

Ответ: 60°.

 

2. Площадь ортогональной проекции многоугольника ABCDEF на некоторую плоскость равна 12 см² . Угол между плоскостями проекций и многоугольника равен 45°. Найдите площадь многоугольника ABCDEF

Решение

По свойству 6.9 cos <α =12/ S _ABCDEF = √2/2, поэтому площадь многоугольника ABCDEF равна см ²

Ответ: см².

 

3. В кубе ABCDA₁B₁C₁D₁ длина ребра равна a. Найдите расстояние между прямыми CB₁ и A₁ B.

 

Решение

Так как отрезки CB₁ и A₁ B – это диагонали, лежащие в смежных гранях куба, то по 6.12 это расстояние равно a√3/3.

 

 

Ответ: a√3/3.

4. На прямой, перпендикулярной плоскости a и пересекающей ее в точке О, взяты точки А и В, такие, что АВ =5. На плоскости взята такая точка Х, что ХА=3, ХВ=4. Вычислите ХО.

Решение

Для правильного выполнения рисунка установим положение отрезка АВ или, что все равно, положение точек А и В относительно плоскости a. Анализируя числовые данные (треугольник АВ Х является прямоугольным) выясняем, что точки А и В находятся по разные стороны от плоскости

AX² – AO² = XB² – OB²

9– x² =16–(5– x)²; 10 x =18; x =1,8.

.

 

Ответ: 2,4

 

 

5. Будем обозначать расстояние от точки A до плоскости a через | A a|. | A a|= d ₁, | B a|= d ₂. Найдите | X a|, если X Î(AB), | AX |:| XB |= p: g.

 

Решение

Проекцией отрезка АВ на плоскость a является отрезок K ₁ K ₂ Þ проекция любой точки отрезка АВ будет принадлежать от резку K ₁ K ₂.

(по условию).

XK = XM + MK = D ₁+ MK

DMAX ~ D NAB (по двум углам) Þ ,

.

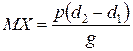
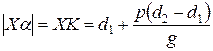Ответ: .

 

6. В основании пирамиды SABC лежит равносторонний треугольник ABC, длина которого 4√2 см, Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. Найдите расстояние между прямыми S E и СD, где точки E и D и– середины ребер BC и AB соответственно.

 

Решение

Построим плоскость, проходящую через точку E, перпендикулярную прямой CD. Это плоскость ELO, проходящая через две прямые LO и EO, перпендикулярные прямой CD. LE – проекция SE на плоскость ELO. Отрезок OP- перпендикуляр к этой проекции. Этот отрезок равен расстоянию между двумя скрещивающимися прямыми (6.6.2). В прямоугольном треугольнике LEO этот отрезок равен высоте этого прямоугольного треугольника: OP = LO·EO:LE,

OE = √2, LO = 2, LE = , тогда OP = 2√3/3.

 

 

7. Определите расстояние между скрещивающимися высотами граней правильного тетраэдра, если ребро его равно a.

Решение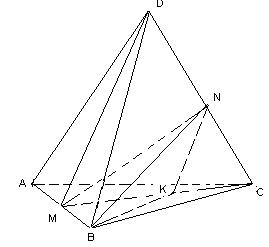

 

Определим расстояние между высотами DM и BN. В плоскости DMC проведем NK||DM. Получим, что расстояние между указанными скрещивающимися прямыми равно расстоянию от любой точки прямой MD до плоскости BNK. Это расстояние будет равно высоте пирамиды с основанием BNK и вершиной M. С другой стороны, в качестве основания пирамиды можно взять треугольник MKB, а вершины – точку N. Вычислим объем этой пирамиды.V = 1/3 S_MKB ·1/2H, где H – высота тетраэдра. Н = a√2/3, S_MKB = ¼ S_ABC = a² √3/16. V = a³ √2/96. Этот же объем можно вычислить, приняв за основание треугольник BKN. Вычислим площадь этого треугольника. Длины его сторон: BM = a √3/2, B K= a √7/4,

NK = a √3/4. Его площадь равна a² √5/16. Тогда высота пирамиды с основанием BNK и вершиной M равна a9√10.

 

Ответ: a9√10.

 

 

Таблица 7

 

Геометрический объект	Многогранный угол	Трехгранный угол
Определение	7.1.Фигура, образованная всеми лучами (SA,SB, SC…), имеющими общее начало (точка S) и пересекающими некоторый многоугольник (ABC…), называется многогранным углом SABC… Общее начало всех лучей (точка S) называется вершиной многогранного угла. Лучи SA, SB, SC… называются ребрами многогранного угла. Углы ASB, BSC, CSD… называются плоскими углами многогранного угла или его гранями. Каждые две грани, имеющие общее ребро(например, грани BSC и CSD имеют общее ребро SC), определяют двугранный угол многогранного угла. Если многоугольник ABCD… является выпуклым, то и многогранный угол SABC… является выпуклым.	7.4 Многогранный угол, имеющий три плоских угла, называется трехгранным
Изображение
Свойства	7.2* Сумма величин всех плоских углов выпуклого многогранного угла меньше 360º. 7.3**.Если в выпуклом четырехгранном угле все плоские углы равны, то плоскости, проходящие через его противоположные ребра, перпендикулярны.	7.5*.Величина каждого плоского угла трехгранного угла меньше суммы величин двух других плоских углов. 7.6*.Если два плоских угла трехгранного угла равны, то их общее ребро проектируется на прямую, содержащую биссектрису третьего плоского угла. 7.7 *.Теорема косинусов. Косинус плоского угла трехгранного угла равен произведению косинусов двух остальных плоских углов, сложенному с произведением синусов этих же углов и косинуса двугранного угла, противолежащего этому плоскому двугранному углу. 7.8 *. Теорема синусов В трехгранном угле синусы плоских углов пропорциональны синусам противолежащих им двугранных углов.   .

 

Задачи

1. В трехгранном угле SABC два плоских угла ASB и ASC равны по 60º, а третий BSC угол равен 90º. AS= 4см. Найдите расстояние от точки A до плоскости BSC.

 

Решение

По свойству 7.2 луч SK - биссектриса угла BSC. Поэтому угол KSC равен 45º.Двугранный угол при ребре SK равен 90º, так как плоскость ASK проходит через перпендикуляр AK к плоскости BSC. К трехгранному углу SAKC применим теорему косинусов:

cos<ASC = cos<ASK cos<KSC + sin<ASK sin<KSC cos90º, подставим данные по условию значения углов, получим: ½ = cos<ASK √2/2,

 

cos<ASK = 1/√2. Тогда AK = AS sin<ASK = .

 

 

Ответ: .

 

2. Все плоские углы многогранного угла равны по 45^° . Найдите косинусы двугранных углов этого трехгранного угла.

 

Решение

Запишем теорему косинусов (7.7) для одного из плоских углов данного трехгранного угла. Получим:

cos45º = cos45º cos45º + sin45º sin45º cos<A, cos<A = √2- 1.

 

Ответ: √2- 1.

 

 

3. Два двугранных угла трехгранного угла равны 60^° и 30^°, плоский угол, противолежащий первому их них, равен 60^°. Найдите синус плоского угла, противолежащего второму двугранному углу.

 

Решение

Запишем теорему синусов (7.8) для данного трехгранного угла: . Откуда получаем, что синус плоского угла, противолежащего второму двугранному углу, равен sin 30^°и равен 0,5.

 

Ответ: 0,5.

4. Найдите косинус двугранного угла правильного тетраэдра.

 

Решение

Все плоские углы трехгранного угла правильного тетраэдра равны по 60º. Применим теорему косинусов (7.6) к одному из трехгранных углов: cos60º = cos60º cos60º + sin60º sin60º cos<A, cos<A = 1/√3.

Ответ: 1/√3.

таблица 8

	Призма	Параллелепипед
Определение	8.1 Призмой (ABCD… A1B1C1D1 …) называется многогранник, две грани которого ABCD… и A1B1C1D1… n-угольники, лежащие в параллельных плоскостях, а остальные грани(АA1BB1…) – параллелограммы Многоугольники (ABCD… и A1B1C1D1), лежащие в параллельных плоскостях, называются основаниями призмы. Грани – параллелограммы называются боковыми гранями Отрезок перпендикуляра (HH1) к основанию призмы, заключенный между основаниями, называется высотой призмы. 8.2 Призма (ABCD… A1B1C1D1 …) называется прямой, если ее боковые ребра перпендикулярны основаниям. Если боковые грани не перпендикулярны основаниям, то призма называется наклонной. 8.3 Призма называется правильной, если она прямая, а основания призмы - правильные многоугольники.	8.4 Параллелепипедом называется призма, основание которой – параллелограмм В параллелепипеде шесть граней и все они параллелограммы. б ) Прямым параллелепипедом называется параллелепипед, боковые ребра которого перпендикулярны плоскости основания в) Прямоугольным параллелепипедом называется прямой параллелепипед, основанием которого служит прямоугольник. Три неравных ребра прямоугольного параллелепипеда (a,b,c) называются его измерениями).
Изображение		Прямой параллелепипед ABCDA1B1C1D1
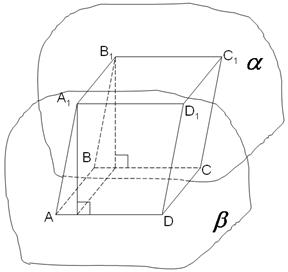
Свойства	В наклонной призме только одна грань может быть перпендикулярна основанию   (АА1D1) ^(АВС) но остальные боковые не перпендикулярны основанию.   В наклонной призме две грани могут быть перпендикулярными основанию (АА1D1) ^ (АВС), (ВВ1С1) ^ (АВС), но (DD1С1) не ^ (АВС), (АА1В1) не ^ (АВС).	8.5. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: d2 = a2+ b2+c2 8.6.Диагонали параллелепипеда точкой пересечения делятся пополам. 8.7 В прямом параллелепипеде четыре попарно равных диагонали. 8.8.Противоположные грани параллелепипеда - равные параллелограммы. 8.9*. В параллелепипеде ABCDA1B1C1D1 проведены сечения A1BC и CB1D1. Эти плоскости делят диагональ AC1 в отношении 1: 1: 1 8.10* Если в наклонном параллелепипеде боковое ребро образует равные углы с смежными ребрами основания, то высота параллелепипеда проектируется на биссектрису угла между этими смежными ребрами. 8.10* a)Если две смежные грани параллелепипеда - равные ромбы,то одно из диагональных сечений этого параллелепипеда – прямоугольник.
	8.12. Около прямой призмы, в основании которой лежит многоугольник, около которого можно описать окружность, можно описать сферу. 8.13.В правильную призму можно вписать сферу, если ее высота равна диаметру сферы. 8.14*. В любую прямую призму, в основание которой можно вписать окружность, радиуса R, и высота которой равна 2 R. Можно вписать сферу. 8.15*. В наклонную призму можно вписать шар, если в ее перпендикулярное сечение можно вписать окружность радиуса R, и высота призмы равна 2 R.	8.11 *.Около любой правильной призмы можно описать сферу.

 

 

Задачи

1. Сколько различных разверток куба можно построить?

 

Шесть разверток с четырьмя гранями в один ряд, четыре развертки с тремя гранями в одну строчку, одна развертка с двумя гранями в одну строчку.

Ответ: 11.

 

2. Найдите кратчайшее расстояние по поверхности прямоугольного параллелепипеда из точки M в точку N (точка M – на передней грани, точка N – на задней грани прямоугольного параллелепипеда)

Решение

Рассмотрим возможные развертки параллелепипеда. Кратчайший путь по поверхности изобразиться на развертке одним из отрезков MN, MC, MD, ME. Определив длину каждого из них, найдем длину.

наименьшего пути. MB ² = 42² , MC² = 37 ² + 17 ² =1658, MD ² = 32 ² + 24 ² =1600, ME>MD. Следовательно, кратчайший путь MD имеет длину 40см.

Ответ: 40 см

 

 

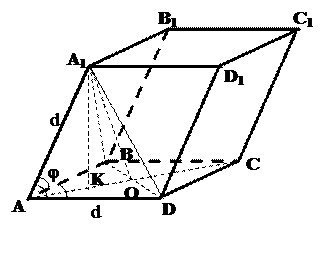3. В параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ все грани – равные ромбы. Острый угол ромба равен j, сторона равна d. Чему равна высота параллелепипеда?

 

Решение

По свойству 8.10 высота параллелепипеда AK будет лежать в плоскости АА₁С.

 

,

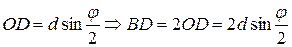
D BA ₁ D – равносторонний; .

Пусть KO = X;

 

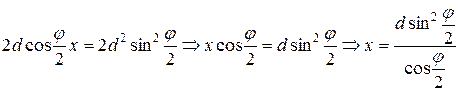
Ответ:

4. Пусть ABCA ₁ B ₁ C ₁ – треугольная призма. ее основанием является равносторонний треугольник ос стороной 2. Ð A ₁ AC =Ð A ₁ AB =60⁰. Найдите высоту призму, если AA ₁ равняется 3.

 

 

, , , .

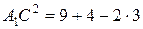Таким образом, ; ; AA ₁=3.

Значит, D ANA ₁ – прямоугольный, Ð N =90⁰, A ₁ N – высота призмы.

 

 

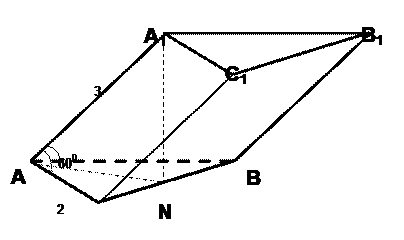
5. Пусть ABCA ₁ B ₁ C ₁ – треугольная призма. ее основанием является равносторонний треугольник ос стороной 2. Ð A ₁ AC =Ð A ₁ AB =60⁰. Найдите высоту призму, если AA ₁ равняется а) 1; б) 2;

Решение: а) 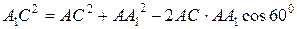(рис.1) , , A ₁ B = A ₁ C, т.к. D CA ₁ B – равнобедренный. . ,

.

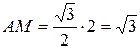б) Если AA ₁=2, то A ₁ ABC является правильным тетраэдром. Высота тетраэдра проектируется в центр описанной окружности около треугольника ABC.(рис.2).

.

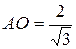A ₁ O – высота призмы.

 

Таблица 9

 

Геометрический объект	Пирамида	Правильная пирамида
Определение	9.1Пирамидой (SABCD…) называется многогранник, у которого одна грань (ABCD…) – какой - нибудь многоугольник, а остальные грани (SAB, SBC, SCD…) – треугольники с общей вершиной (S) Боковыми гранями пирамиды называются треугольники с общей вершиной (∆SAB, ∆SBC, ∆SCD…). 9.2Вершина пирамиды(S) – общая вершина боковых граней. Основание пирамиды – многоугольник (ABCD…). 9.3Боковыми ребрами пирамиды называются ребра, идущие из вершины (SA, SB, SC..). 9.4Высота пирамиды – перпендикуляр, проведенный из вершины к основанию (SO). 9.5Тетраэдр – треугольная пирамида	9.10.Правильной пирамидой называется пирамида, в основании которой правильный многоугольник, а высота проектируется в центр основания. 9.11.Апофемой называется высота боковой грани правильной пирамиды, проведенная к стороне основания
Изображение		SM – апофема.
Свойства	9.6*.Если все боковые ребра пирамиды равны, то ее высота проектируется в центр окружности, описанной около основания. 9.7*. Если все двугранные углы при основании пирамиды равны, то ее высота проектируется в центр окружности, вписанной в основание. 9.8*Теорема Чевы Пусть точка M внутри тетраэдра ABCD, точки A1 , B1 , C1, D1 – точки пересечения плоскостей CMD, AMD, AMB, CMB с ребрами AB, BC, CD, DA соответственно. Тогда 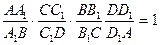, Справедливо и обратное: если для точек A1 , B1 , C1, D1 , лежащих на соответствующих ребра, выполнено соотношение 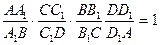, то плоскости CA 1 D, CD 1 B, AC 1 B, AB 1 D проходят через одну точку. 9.9*Если плоскость α пересекает ребра AB, BC, CD, DA тетраэдра ABCD в точках A1, B1, C1, D1, то 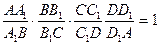Обратно, если для четырех точек A1, B1, C1, D1, лежащих соответственно на ребрах AB, BC, CD, DA тетраэдра ABCD выполнено равенство 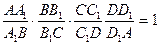, то эти четыре точки лежат в одной плоскости.	9.11.Боковые ребра правильной пирамиды равны. 9.12.Боковые грани правильной пирамиды – равные равнобедренные треугольники. 9.13.Противоположные ребра правильной треугольной пирамиды перпендикулярны. 9.14** a).Если противоположные ребра тетраэдра перпендикулярны, то ее высота проектируется в ортоцентр основании я (точку пересечения высот пирамиды). b).Если противоположные ребра тетраэдра перпендикулярны, то суммы их квадратов равны. 9.15 **. В треугольной пирамиде, у которой все ребра равны (в правильном тетраэдре) высоты пересекаются в одной точке и делятся ей в отношении 3:1, считая от вершины. Высота правильного тетраэдра с ребром a равна . Центры шаров: вписанных в правильный тетраэдр, описанных около правильного тетраэдра, касающегося всех его ребер, совпадают с точкой пересечения его высот.
Примечания	9.16*a).Около любой треугольной пирамиды можно описать сферу. b).В любую треугольную пирамиду можно вписать шар с) Если около основания пирамиды можно описать окружность, то около пирамиды можно описать сферу.	9.17*.а) Около любой правильной пирамиды можно описать сферу. . 9.17.* В любую правильную пирамиду можно вписать шар.

 

Задачи

 

1. Пусть точка M внутри тетраэдра ABCD, точки A₁ , B₁ , C₁– точки п