Закон Ома для всей цепи
Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис.1), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:
.
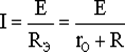Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
, где m – число ветвей подключенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1) I - I1 - I2 = 0.
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
,
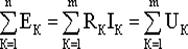где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rк в контуре; Uк = RкIк – напряжение или падение напряжения на к-м элементе контура.
Магнитное поле и его характеристики и свойства
Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.
|
|
Графическое изображение магнитного поля. Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец постоянного магнита, из которого выходят силовые линии (рис. 35, а), принято считать северным полюсом, а противоположный конец, в который входят силовые линии,— южным полюсом (силовые линии, проходящие внутри магнита, не показаны). Распределение силовых линий между полюсами плоского магнита можно обнаружить при помощи стальных опилок, насыпанных на лист бумаги, положенный на полюсы (рис. 35, б). Для магнитного поля в воздушном зазоре между двумя параллельно расположенными разноименными полюсами постоянного магнита характерно равномерное распределение силовых магнитных линий (рис. 36) (силовые линии, проходящие внутри магнита, не показаны).
Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б).
|
|
Рис. 35. Магнитное поле, созданное постоянным магнитом.
Рис. 36. Однородное магнитное поле между полюсами постоянного магнита.
Рис. 37. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий.
Для более наглядного изображения магнитного поля силовые линии располагают реже или гуще. В тех местах, где магнитное роле сильнее, силовые линии располагают ближе друг к другу, там же, где оно слабее,— дальше друг от друга. Силовые линии нигде не пересекаются.
Во многих случаях удобно рассматривать магнитные силовые линии как некоторые упругие растянутые нити, которые стремятся сократиться, а также взаимно отталкиваются друг от друга (имеют взаимный боковой распор). Такое механическое представление о силовых линиях позволяет наглядно объяснить возникновение электромагнитных сил при взаимодействии магнитного поля и Проводника с током, а также двух магнитных полей.
Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля.
6.
5. 
Рисунок 2 — Разветвленная цепь
Неразветвленные и разветвленные электрические цепи.
В неразветвленной цепи рис. 1 протекает один и тот же ток.
В разветвленной ветви в каждой ветви протекает свой ток.Ветвь можно определить, как участок цепи,образованный последовательно соединенными элементами, заключенными между двумя узлами. А узел,соответственно, есть точка цепи, в которой сходится не менее трех ветвей.Если в месте пересечения двух линий на электрической схеме есть точка рис.3, то в этом месте существует электрическое соединение двух линий. В противном случае, когда нет точки в месте пересечения двух линий рис.4, значит нет соединения, а линии только пересекаются. Напряжение на участке цепи.
|
|
Под напряжением на некотором участке электрической цепи понимают разность потенциалов междукрайними точками этого участка. На участке рис.5 крайние точки которого обозначены буквами «а» и «в».Пусть ток I течет от точки «а»большего потенциала к точке «в» меньшего потенциала. Следовательно,потенциал точки «а» (Yа) увеличение потенциала точки «в» (Yв) на величину, равную произведению тока Iна сопротивление R:Yа=Yв + IR
В соответствии с определением напряжение между точками «а» «в»:
Uaв = Y а= Yв
Отсюда Uaв=IR, т.е. напряжение на сопротивлении равно произведению тока, протекающего посопротивлению, на величину этого сопротивления.
По виду магнитные цепи делятся на неразветвлённые и разветвлённые, а по структуре на однородные и неоднородные.
Неразветвлённой магнитной цепью называют такую цепь, через элементы которой проходит один и тот же магнитный поток. В разветвлённой разветвлённоймагнитнойцепи содержатся участки (ветви), в которых поток различен.
Если в разветвлённой цепи есть точка, в которой сходятся участки с различными потоками, то для такой точки (узла цепи) справедлив первый закон Кирхгофа для магнитной цепи, утверждающий что алгебраическая сумма магнитных потоков, сходящихся в узле, равна нулю:
.
Для замкнутого контура магнитной цепи можно применять второй закон Кирхгофа, по которому алгебраическая сумма падений магнитных напряжений равнаалгебраической сумме МДС,
где Iw – МДС, равная произведению намагничивающего тока I на число витков катушки w, обозначаеться МДС можно буквой F.
Вопрос 7
Синусоидальный ток и его характеристики; изображение синусоидальных величин с помощью временных и векторных диаграмм
Синусоидальный ток представляет собой функцию времени. То есть в отличие от постоянного тока его значение меняется с течением времени. Основными характеристиками синусоидального тока являются: амплитуда частота и начальная фаза.
Частота f это количество колебаний в единицу времени. За единицу времени в системе СИ принимается одна секунда. Таким образом, количество колебаний за секунду это и есть частота синусоидального тока. И измеряется она в Герцах. Названа в честь ученого Герца. Величина обратная частоте называется периодом колебания T=1/f. Период измеряется в секундах. Определение периода звучит так период это время полного колебания. Если представить себе маятник часов то период это время за которое он совершит движение из одного крайнего положения в другое и обратно.
Амплитуда с инусоидального тока это максимальное значение тока, которое он достигает за период колебания. Опять же если рассматривать на примере маятника, то амплитуда это расстояние от положения равновесия до одного из крайних положений.
Начальная фаза синусоидального тока это то время, на которое отстает либо опережает синусоида начальный момент времени.
Представим две синусоиды одна, из которых начинается условно в нуле а другая в 1. То можно сказать, что вторая синусоида отстаёт по фазе от первой. Если обе синусоиды начинаются в одной точке то можно сказать что они синфазные, то есть имеют одну фазу. При этом они обе могут отставать от начального момента времени на одну и ту же величину, то есть иметь одинаковую начальную фазу.
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
Математически синусоидальный ток описывается уравнением:
i=Im*sin(wt+j)
где
i мгновенное значение тока это величина тока в определенный момент времени с учетом частоты и начальной фазы тока.
Im амплитуда тока.
j начальная фаза
w угловая частота выражается как
