Рис. 1 — Графическое представление синусоидального тока
Векторной диаграммой называется совокупность нескольких векторов, изображённых синусоидальные величины одинаковой частоты в начальный момент времени.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
|
Пусть, например, в точке разветвления цепи (рис. 5) общий ток 
равен сумме токов 
и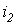 
двух ветвей: 
.
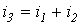Каждый из этих токов синусоидален и может быть представлен уравнением
и 
.
Результирующий ток также будет синусоидален:
.
Определение амплитуды 
и начальной фазы 
этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. 
На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным 
.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты:
Вопрос №8
Электрическая цепь с активное сопротивление, его векторная диаграмма 
Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 56), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и направление тока. Это значит, что ток и напряжение совпадают по фазе.
В активном сопротивлении напряжение и ток совпадают по фазе, поэтому векторы напряжения Ū R и тока Ī направлены в одну сторону. Они могут лежать на одной прямой или на параллельных прямых. При этом связка векторов Ū R и Ī может иметь произвольное направление, но во всех случаях угол между векторами равен нулю.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отложим в выбранном масштабе по горизонтали вектор напряжения 
. Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (φ = 0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Вопрос №9