Коэффициент мощности и баланс мощностей

В формуле (2.25) присутствует сомножитель который называют коэффициентом мощности. Он показывает, какая доля активной мощности содержится в полной, подводимой к потребителю мощности S, то есть = Р / S.

На практике, при передаче электрической энергии от источника к потребителю, стремятся обеспечить максимальное значение коэффициента мощности, чтобы → 1. Причиной уменьшения является наличие в потребителе реактивных сопротивлений, в основном индуктивного характера, обуславливающих появление сдвига фаз φ между напряжением и током и появление реактивной составляющей тока. Из-за этого появляется реактивная мощность, которая приводит к неполному использованию генераторов, линий передачи электрической энергии, трансформаторных подстанций и другого электротехнического оборудования. Все это является причиной увеличения потерь электроэнергии.

Для увеличения cosφ используют различные способы компенсации сдвига фаз φ. Наиболее простым из них является подключение параллельно нагрузке батареи конденсаторов. При этом, если емкостная проводимость конденсаторов будет равна индуктивной проводимости потребителя, они взаимно компенсируются. Реактивная составляющая общего тока в подводящей линии передачи электрической энергии снижается, и сдвиг фаз φ между напряжением и током приближается к нулю. Коэффициент мощности будет близок к единице.

Баланс мощностей

В электрической цепи в любой момент времени алгебраическая сумма мгновенных мощностей источников энергии р_И равна алгебраической сумме мгновенных мощностей приемников энергии р_П :

(2.31)

 

Это утверждение вытекает из закона сохранения энергии.

Для цепей синусоидального тока баланс мощностей удобно формулировать в комплексной форме:

 

(2.32)

 

В формуле (2.32) для любого источника 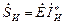и любого потребителя .

Для цепей постоянного тока

 

(2.33)

 

В формуле (2.33) E_k I_k – мощность k – го источника из всех п источников, а U_l I_l – мощность l – го потребителя из всех т потребителей данной цепи.

 

 

13.

Резонанс напряжений - явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.

Условия возникновения резонанса:

1. Последовательное соединение L и C с генератором переменного тока;

2. Частота генератора должна быть равна частоте собственных колебаний контура, при этом характеристические сопротивления равны;

3. Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.

Полное сопротивление цепи:

_c)² = R _ом.,

так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.

При максимальном значении тока напряжения на участках L и C будут большими и равными между собой.

Напряжение на зажимах цепи:

.

Рассмотрим следующие соотношения:

, следовательно

.

Q – добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура

резонанса.

Пример:

Если добротность равна 100, напряжение на зажимах 1В, то

Uc=Ul=QU =100В,

то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений.

При резонансе, коэффициент передачи равен добротности.

Построим векторную диаграмму напряжения.

Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.

Рассмотрим энергетический процесс в колебательном контуре:

В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.

Докажем это математически:

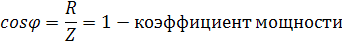
, полная мощность цепи, которая равна активной мощности.

, реактивная мощность обмена цепи с генератором.

Q _вн = I _o²(L/C)^0.5, реактивная мощность, циркулирующая в LC -контуре.

где (L/C)^0.5 - характеристическое (волновое) сопротивление контура.

14. Рассмотрим разветвленную цепь, параллельно соединённых катушки индуктивности L (с активным сопротивлением R) и конденсатора С (рис. 2.29).

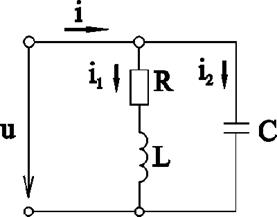
Рис.2.29. Электрическая схема разветвлённой цепи

 

Пусть мгновенные значения напряжения и тока цепи изменяются по синусоидальному закону 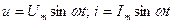. По первому закону Кирхгофа , для действующих значений токов . По закону Ома . Из треугольника сопротивлений, для последовательно соединённых R и L, 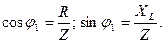Разложим токи в ветвях на активные и реактивные составляющие IR, IL, IC и определим их значения: .

Введем следующие обозначения:

= g (2.25)

- активная проводимость первой ветви;

(2.26)

- реактивная индуктивная проводимость первой ветви;

(2.27)

- реактивная емкостная проводимость второй ветви.

Для случая IL > IC построим векторную диаграмму (рис. 2.30):

Из векторной диаграммы находим общий ток:

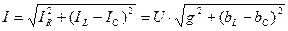, (2.28)

где

(2.29)

- полная проводимость цепи.

 

Рис.2.30. Векторная диаграмма разветвлённой цепи переменного тока

 

Из векторной диаграммы следует, что наличие ёмкости снизило вектор действующего значения тока 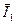до величины , а cosφ при этом увеличился. Резонанс токов можно практически получить изменением ёмкости конденсатора. На рис.2.31 приведены примерные графические зависимости IL, IC, I, cosφ от изменения C, где Cp - резонансная ёмкость.

 

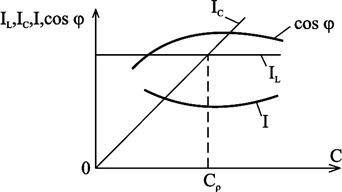
Рис.2.31. Примерное изображение зависимостей IL, IC, , cos от изменения ёмкости конденсатора C

 

Рис.2.32. Треугольник проводимостей цепи

 

Выражение (2.29) соответствует треугольнику проводимостей цепи, представленному на рис. 2.32, откуда следует:

; (2.30)

 

. (2.31)

Выражения для мощностей принимают такой вид:

(2.32)

- активная мощность,

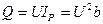(2.33)

- реактивная мощность,

(2.34)

- полная мощность.

Резонансом токов для рассматриваемой цепи называют явление, при котором ток IL = IC, тогда общий ток I в неразветвленной части цепи совпадает по фазе с напряжением источника. При резонансе токов = 0; cos = 1; bL = bC; I = IR. Пусть резонансная частота f0 определяется из соотношения 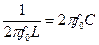, тогда , а угловая резонансная частота .

Итак, признаками резонанса токов являются:

а) индуктивная и емкостная проводимости равны;

б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и имеет минимальное значение;

в) коэффициент мощности максимален.

 

15. Электрические фильтры могут применяться для сглаживания пульсаций напряжения выпрямителей, демодуляторов, которые преобразуют модулированные по амплитуде колебания высокой частоты в относительно медленные изменения напряжения сигнала, и в других подобных устройствах.

В самом простейшем случае можно ограничиться включением последовательно с нагрузкой катушки индуктивности, сопротивление которой увеличивается с возрастанием порядка гармонической и сравнительно невелико для низкочастотных колебаний, и тем более для постоянной составляющей. Более эффективно применение П-образных, Т-образных и Г-образных фильтров.

На рис. 1 показана схема простого Г-образного фильтра с катушкой индуктивности L и конденсатором С, включенными между приемником rпр и выпрямителем В. Переменные токи всех частот встречают значительное сопротивление катушки индуктивности, а включенный параллельно конденсатор пропускает по параллельной ветви остаточные токи высоких частот. Благодаря этому значительно уменьшаются пульсации напряжения на нагрузке rпр. Могут применяться и фильтры, состоящие из двух и более подобных звеньев. Иногда используются упрощенные фильтры с резисторами вместо катушек индуктивности.

Рис. 1. Простейший сглаживающий Г-образный электрический фильтр

Более совершенными являются резонансные фильтры, в которых используются явления резонанса. При последовательном соединении катушки индуктивности и конденсатора, когда fωL= 1/(кωС), цепь будет иметь наибольшую проводимость (активную) при частоте fω и достаточно высокие проводимости в полосе частот, близких к резонансной. Такая цепь является простым полосовым фильтром. При параллельном соединении катушки индуктивности и конденсатора такая цепь будет иметь наименьшую проводимость при резонансной частоте и относительно малые проводимости в полосе частот, близких к резонансной. Такой фильтр является заградительным для некоторой полосы частот.

Для улучшения характеристики простого полосового фильтра можно применять схему (рис. 2), в которой параллельно приемнику включены параллельно друг другу катушка индуктивности и конденсатор. Такая цепь настроена также в резонанс на частоту коз и представляет очень большое сопротивление для токов выбранной полосы частот и значительно меньшее сопротивление — для токов других частот.

Рис. 2. Схема простого полосового электрического фильтра

Подобный фильтр может применяться в модуляторах, которые выдают модулированные колебания определенной частоты. На модулятор М подается напряжение Uc сигнала низкой частоты, которое преобразовывается в модулированные колебания высокой частоты, а фильтр выделяет напряжение требуемой частоты, которое подается на нагрузку rпр.

Зависимость модуля комплексного коэффициента передачи от частоты называется передаточная АЧХ, - передаточная АЧХ.

Зависимость аргумента комплексного коэффициента передачи от частоты называется передаточная ФЧХ, - передаточная ФЧХ.

Модуль коэффициента передачи изменяется от 0 до 1.

 

АЧХ Амплитудно-частотная характеристика определяет характер изменения коэффициента усиления, или выходного сигнала усилителя при изменении частоты сигнала.
АЧХ представляет собой график зависимости выходного напряжения (или коэффициента усиления), величина которого откладывается по оси координат, от частоты, откладываемой по оси абсцисс.. Это приводит к эффективному расширению низкочастотного и сжатию высокочастотного участков на оси частот.

Фазовые характеристики фильтра Чебышёва I рода Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.

 

 

17. Трёхфазная система электроснабжения — частный случай многофазных систем электрических цепей переменного тока, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый фазовый угол. В трёхфазной системе этот угол равен 2π/3 (120°).

Многопроводная (шестипроводная) трёхфазная система переменного тока изобретена Николой Тесла. Значительный вклад в развитие трёхфазных систем внёс М. О. Доливо-Добровольский, который впервые предложил трёх- и четырёхпроводную системы передачи переменного тока, выявил ряд преимуществ малопроводных трёхфазных систем по отношению к другим системам и провёл ряд экспериментов с асинхронным электродвигателем.

 

Схемы соединений трехфазных цепей[править | править вики-текст]

См. также: Трансформатор § Схемы и группы соединения обмоток трёхфазных трансформаторов

Звезда [править | править вики-текст]

Звездой называется такое соединение, когда концы фаз обмоток генератора (G) соединяют в одну общую точку, называемую нейтральной точкой или нейтралью. Концы фаз обмоток потребителя (M) также соединяют в общую точку.

Провода, соединяющие начала фаз генератора и потребителя, называются линейными. Провод, соединяющий две нейтрали, называется нейтральным.

Трёхфазная цепь, имеющая нейтральный провод, называется четырёхпроводной. Если нейтрального провода нет — трёхпроводной.

Если сопротивления Za, Zb, Zc потребителя равны между собой, то такую нагрузку называют симметричной.

{\displaystyle P=3U_{F}I_{F}cos\varphi =3{\frac {U_{L}}{\sqrt {3}}}I_{L}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi }

18, Треугольник

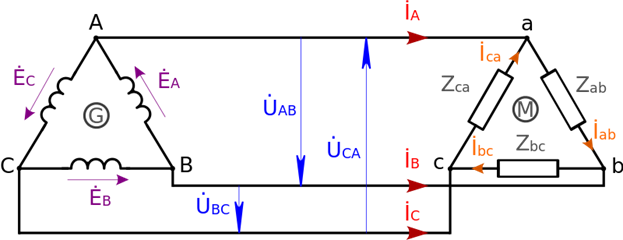
{\displaystyle u_{L}^{ab}=u_{F}^{a}-u_{F}^{b}=U_{F}[\cos(\omega t)-\cos(\omega t-2\pi /3)]=2U_{F}\sin(-\pi /3)\sin(\omega t-\pi /3)={\sqrt {3}}U_{F}\cos(\omega t+\pi -\pi /3-\pi /2)}

{\displaystyle u_{L}={\sqrt {3}}U_{F}\cos(\omega t+\pi /6)}

Треугольник — такое соединение, когда конец первой фазы соединяется с началом второй фазы, конец второй фазы с началом третьей, а конец третьей фазы соединяется с началом первой.