Задания по программированию на Паскале
ВВЕДЕНИЕ
Основными целями лабораторного практикума по курсу «Информатика» являются:
· овладение одним из наиболее распространенных языков программирования;
· изучение и освоение основных методов и приемов алгоритмизации и программирования;
· получение практических навыков работы на компьютерах, отладки и тестирования программ.
Содержатся индивидуальные задания для самостоятельных лабораторных работ по основам алгоритмизации и программирования. В указаниях рассматриваются следующие темы: программирование линейных, разветвленных и циклических алгоритмов; обработка массивов.
Требования к оформлению лабораторных работ.
Лабораторные работы оформляются в тетради в виде отчета, который должен содержать:
1. Математическую формулировку задачи.
2. Блок-схему алгоритма.
3. Текст программы.
4. Исходные данные. Результаты.
Алгоритмы линейной структуры.
Задание. Разработать, ввести в ЭВМ и отладить программу для расчета
Вариант 1.
1. Найти длину окружности и площади круга по заданному радиусу.
2. Даны x и y. Вычислить a,b, если
, 
.
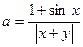Вариант 2.
1. Вычислить процент выполнения плана предприятием, если известны плановый и фактический выпуск продукции.
2. Вычислить объем и площадь поверхности цилиндра по заданному диаметру и высоте.
Вариант 3.
1. Рассчитать среднюю загруженность членов бригады при известном общем объеме работ(в часах) и количестве рабочих.
2. Вычислить среднее арифметическое и среднее геометрическое n действительных чисел.
Вариант 4.
1. Вычислить сумму вклада в банке, если известны начальная сумма, годовой процент, срок хранения.
2. Вычислить объем и площадь полной поверхности круглого конуса по заданным высоте и диаметру основания.
Вариант 5.
1. Вычислить количество гектаров, которое нужно убрать каждой из студенческих групп, если известна общая площадь поля и количество студентов в каждой группе.
2. Вычислить площади кольца по заданным радиусам внутренней и внешней окружностей.
Вариант 6.
1. Вычислить количество единиц товара, которое может приобрести покупатель, и сдачи, если известна сумма и стоимость одной единицы товара.
2. Вычислить количество кусков обоев известных размеров, которое понадобится для оклейки стен в комнате, если даны периметр комнаты и ее высота.
Вариант 7.
1. Вычислить процент успеваемости группы, если известно общее число студентов в группе и количество студентов, получивших «отлично», «хорошо» и «удовлетворительно».
2. Рассчитать времени, за которое катер пройдет данное расстояние против течения и по течению, если известны скорость катера в стоячей воде и скорость течения.
Вариант 8.
1. Вычислить действительное расстояния между городами, если известно расстояние между ними на карте и масштаб карты.
2. Даны длины ребра параллелепипеда. Найти объем и площадь поверхности параллелепипеда.
Вариант 9.
1. Вычислить новую цену товара после трех последовательных повышений, если известны старая цена и процент повышения для каждого раза.
2. Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
Вариант 10.
1. Вычислить объем шара известного радиуса.
2. Даны стороны треугольника, найти его площадь.
Вариант 11.
1. Найти объем налитой в стакан жидкости, если известны высота столба жидкости, и диаметр внутренней окружности стакана.
2. Даны a и b – катеты прямоугольного треугольника, найти его площадь.
Вариант 12.
1. Вычислить длину вектора, выходящего из начала координат по известным координатам конца вектора.
2. Даны x, y. Вычислить a,b, если
, 
.
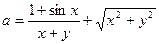Разветвленные алгоритмы
Задание. Написать программу решения следующей задачи.
Вариант 1.
1. Определить и вывести на печать номер квадранта, в котором расположена точка М(x,y).
2. Определить является ли значение целочисленной переменной X кратным восьми.
Вариант 2.
1. Сравнить между собой значения величин X и Y, вывести на печать результат в виде «X > Y», «X < Y» или «X = Y».
2. Определить является ли значение целочисленной переменной X кратным шести.
Вариант 3.
1. Из величин, определяемых выражениями А=sin(x), B=cos(x),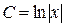 
при заданном х, определить и вывести на печать имя минимальной величины и ее значение.
2. Определить является ли значение целочисленной переменной X кратным четырем.
Вариант 4.
1. Определить, какая из двух фигур (круг или квадрат) имеет большую площадь. Сторона квадрата и радиус круга заданы. Вывести на печать имя минимальной величины и ее значение.
2. Определить является ли значение целочисленной переменной X кратным семи.
Вариант 5.
1. Определить, попадает ли точка М(x,y) в круг с радиусом R и центром в начале координат.
2. Определить является ли значение целочисленной переменной X кратным двум.
Вариант 6.
1. Определить, поместится ли квадрат в круг, если заданы их площади.
2. Определить является ли значение целочисленной переменной X кратным трем.
Вариант 7.
1. Определить, является ли «счастливым» трамвайный билет с шестизначным номером, («счастливым» считается билет, у которого сумма первых трех чисел номера совпадает с суммой трех последних чисел).
2. Определить является ли значение целочисленной переменной X кратным пяти.
Вариант 8.
1. Определить, является ли заданный год високосным.
2. Определить является ли значение целочисленной переменной X кратным шести.
Вариант 9.
1. Определить, поместится ли в круг квадрат, если заданы их площади.
2. Определить, является ли целое число Х кратным трем.
Вариант 10.
1. Определить попадает ли точка М(х,y) в круг с радиусом R и центром в точке A(a,b).
2. Определить, является ли значение целочисленной переменной X кратным девяти.
Вариант 11.
1. Определить, являются ли три числа А, В, С последовательными членами арифметической прогрессии.
2. Определить, какая из точек A(х1,y1,z1) или B(x2,y2,z2) расположена ближе к началу координат.
Вариант 12.
1. Определить являются ли три числа A, B, C последовательными членами геометрической прогрессии.
2. Определить является ли значение целочисленной переменной X кратным шести.
Циклические алгоритмы
Задание. Написать программу решения следующей задачи.
Вариант 1.
1. Вычислить сумму первых m натуральных чисел.
Вариант 2.
1. Составить программу, позволяющую вывести первые N чисел Фибоначчи. (Последовательностью чисел Фибоначчи называется последовательность, в которой первый и второй члены равны единице, а каждый последующий член является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21,...).
Вариант 3.
1. Вычислить таблицу значений функции 
, если х изменяется от х0 до хmax с шагом Dx.
Вариант 4.
1. Найти все двузначные числа, которые делятся на 11.
Вариант 5.
1. Найти квадрат суммы первых k натуральных чисел.
Вариант 6.
1. Вычислить сумму квадратов первых k натуральных чисел.
Вариант 7.
1. Найти все двузначные числа, которые кратны семи.
Вариант 8.
1. Составить таблицу значений функции y = (e 2x + e -x)sin x2, если х изменяется от хmin до хmax с шагом Dx.
Вариант 9.
1. Среди натуральных чисел, больших числа а, но меньших числа b, найти все числа, кратные шести.
Вариант 10.
1. Вычислить N! (N - натуральное число).
Вариант 11.
1. Вычислить 2N! (N- натуральное число).
Вариант 12.
1. Вычислить значения функции y=sin(nx)*cos(nx), если n задано, а x изменяется от x0 до xk с шагом m.
Вариант 13.
1. Найти сумму всех натуральных чисел, больших x, но меньших y.