S – параметры рассеяния»
Выполнил:
студент 4 курса
физического факультета
направления «Радиофизика»
Борисов Никита Владимирович
Воронеж. 2011
СОДЕРЖАНИЕ:
Диаграмма Смита…………………………………………………………....3
S – параметры рассеяния……………………………………………………7
Список Литературы………………………………………………………….9
Диаграмма Смита.
Диаграмма Смита - это мощное вспомогательное средство расчета СВЧ цепей. Кроме чисто практического значения, она дает понимание принципа согласования комплексных сопротивлений и многое другое.
Диаграмма Смита - это бесконечная комплексная плоскость, свернутая с помощью конформного отображения в плоскость, ограниченную единичным кругом. В основе построения диаграммы Смита лежит соотношение:
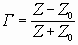(1.1),
где Г - коэффициент отражения, модуль и фаза,
Z - полное сопротивление (например, входное),
Zo - полное характеристическое сопротивление линии передачи.
Пусть относительное сопротивление Z/Zo состоит из активной и реактивной части
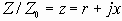(1.2)
и
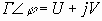. (1.3)
Представляя коэффициент отражения в декартовой системе координат мы хотим построить линии равного Z на плоскости Г. Подставляя (1.2) и (1.3) в (1.1), имеем:
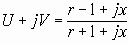(1.4)
Выделяя действительную и мнимую часть справа (1.4), получаем:
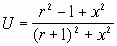(1.5а) 
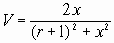(1.5b)
Исключив из этой системы уравнений x, получим уравнение:
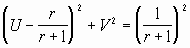(1.6),
представляющее семейство окружностей с центрами в точках
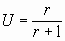, V=0 и с радиусом 
. (1.7)
Исключив из этой системы r, получим уравнение
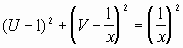, (1.8)
представляющее семейство окружностей (Рис. 1.1):
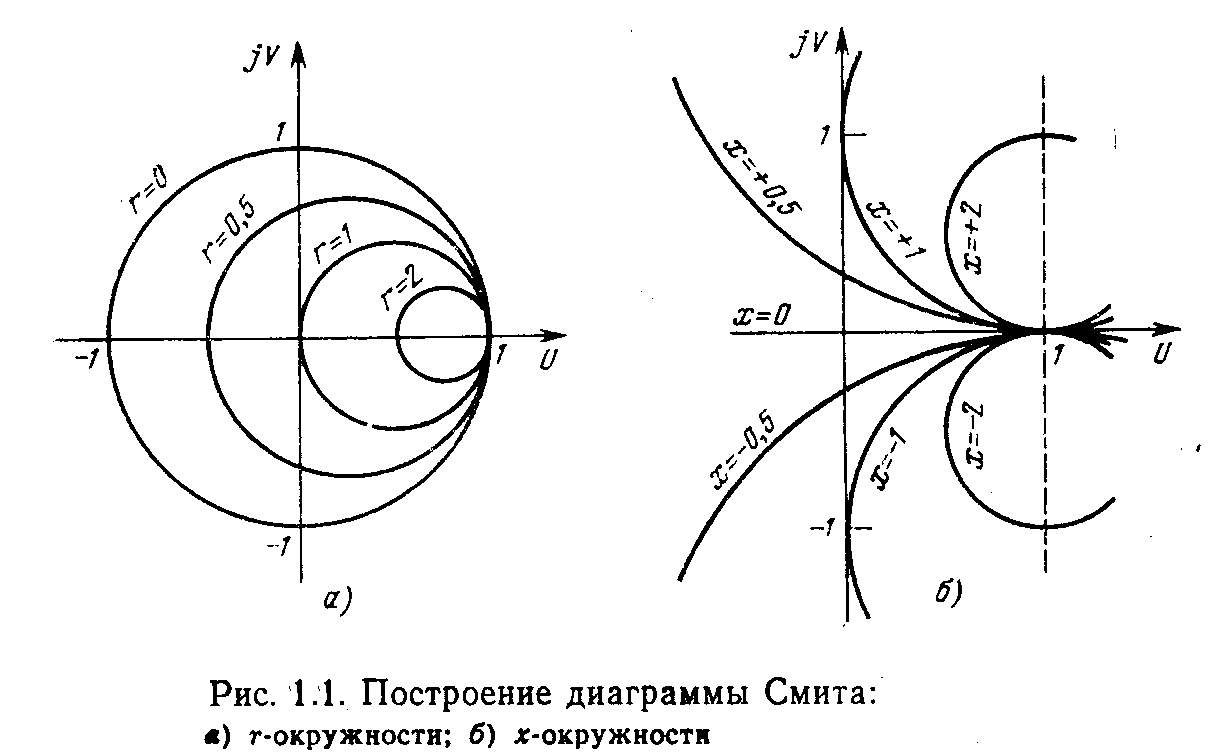
В результате построения этих окружностей для всевозможных r и x, получается диаграмма Смита:
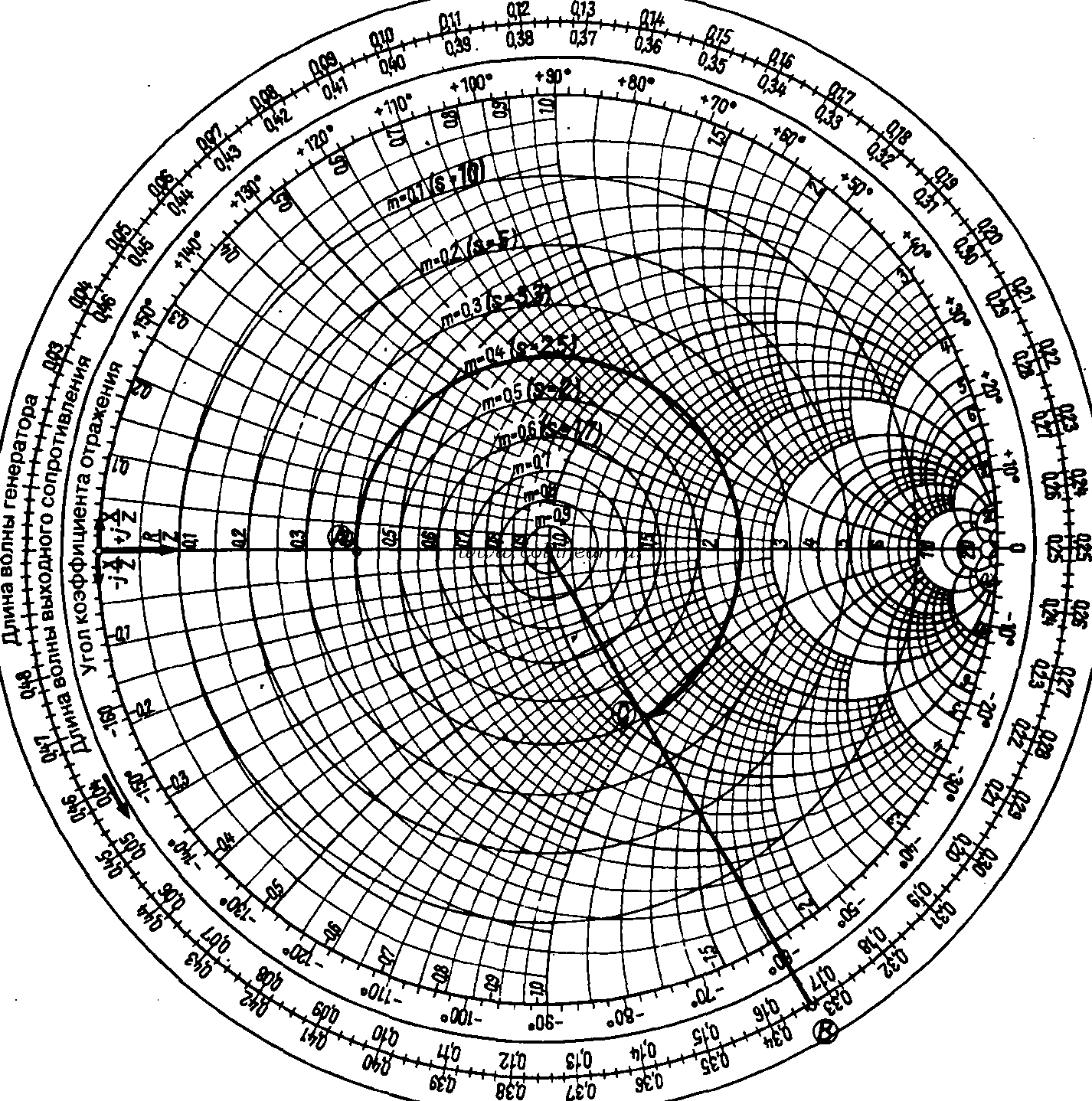
Рис.1.2.диаграмма Смита.
Описание диаграммы.
Круговая диаграмма представляет собою две окружности — внешнюю и внутреннюю, внутри которых расположены два семейства ортогональных окружностей, соответствующих геометрическим местам точек нормированных сопротивлений.
Применение нормированных сопротивлений позволяет применять диаграмму для измерения полных сопротивлений, включенных в линии передачи с любым волновым сопротивлением. На внешней окружности по направлению движения часовой стрелки отложены безразмерные значения отношения L0/λ, пропорциональные фазовому углу, на внутренней окружности те же значения отложены против движения часовой стрелки.
Внешней окружностью следует пользоваться в том случае, когда расстояние до первого минимума L0 отсчитывается по направлению к генератору, внутренней — при отсчете L0 от генератора по направлению к нагрузке. По вертикальному диаметру отложены значения R/ρ, соответствующие проходящим через них окружностям равных нормированных активных сопротивлений.
В местах пересечения окружностей равных нормированных реактивных сопротивлений с внешней окружностью помещены значения Х/ρ: в левой половине диаграммы отрицательные, в правой — положительные. На диаграмме штриховой линией нанесены окружности, проходящие через деления шкалы R/ρ, с центром в точке R/ρ = 1. По этим окружностям отсчитываются значения КБВ и КСВ, так как шкала нормированных активных сопротивлений от 0 до 1 на оси нулевых реактивных сопротивлений одновременно является шкалой КБВ, а от 1 до ∞ — шкалой КСВ.
Работа с диаграммой.
Полное сопротивление определяют в следующем порядке. Из графика, полученного с помощью измерительной линии, характеризующего режим измеряемого тракта, определяют длину отрезка L0, длину волныλ и коэффициент KБВ или KСВ; вычисляют L0/λ. Центр диаграммы (точка R/ρ = 1) соединяют прямой линией (прозрачной линейкой) с внешней или внутренней окружностью, в зависимости от перемещения минимума к генератору или к нагрузке относительно положения его при коротком замыкании в точке L0/λ.
На диаграмме отмечают точку пересечения прямой и окружности KБВ с двумя ортогональными окружностями R/ρ и Х/ρ. Значения R/ρ и Х/ρ, соответствующие этому пересечению, после умножения на ρ дают ответ на поставленную задачу, так как ZНагр = R + jX.
S – параметры рассеяния.
Матрица рассеяния — матрица, элементы которой описывают физические параметры рассеяния. В технике СВЧ матрица рассеяния связывает линейной зависимостью падающую и отражённую волны на входах многополюсника.
При расчёте параметров устройств на СВЧ геометрические размеры устройств становятся соизмеримы с длиной волны и все процессы, протекающие в устройствах, приобретают волновой характер. Для описания параметров можно не принимать во внимание внутреннюю структуру устройства, а ограничиться лишь внешними характеристиками. Таким образом целесообразно любое устройство СВЧ представлять в виде многополюсника, каждый из входов которого представляет собой определённый тип волны, распространяющейся в определённой входной линии. Для упрощения анализа полагают, что в каждой физической линии передачи распространяется лишь основной тип волн.
Каждый вход описываемогомногополюсника в технике СВЧ принято представлять в виде линии передачи с основным типом волн. Следовательно, на каждом входе многополюсника существуют как падающая a, так и отражённая b волны. Отраженные волны связаны с падающими линейными зависимостями.
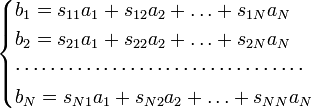
Если представить падающие и отражённые волны на входах многополюсника в виде векторов a и b:
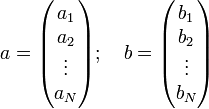
В этом случае линейные зависимости, указанные выше, можно записать в матричной форме
Здесь S - матрица рассеяния.
Физический смысл.
Чтобы определить физический смысл элементов матрицы, необходимо на вход n подать падающую волну, а ко всем остальным входам подключить согласованную не отражающую нагрузку
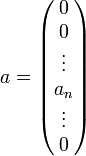
Тогда bm = smnan, откуда
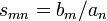
Таким образом, элементы матрицы рассеяния представляют собой коэффициенты передачи со входа n на вход m, при n ≠' m и коэффициенты отражения, если n = m (главная диагональ)
Область применимости.
В отличие от матриц сопротивлений (проводимостей), а также матриц передачи, матрица рассеяния определена для всех устройств СВЧ. Кроме того, с инженерной точки зрения процесс измерения S -параметров возможен для любых устройств СВЧ, так как он сводится к измерению параметров падающей и отражённой волны на входах устройства.
Список литературы:
1) Баскаков С.И. Радиотехнические цепи с распределенными параметрами — М: Высш. школа, 1980
2) Справочник по теоретическим основам радиоэлектроники. Под.ред. Б. Х. Кривицкого. В 2-х т. — М: Энергия, 1977
3) Сазонов Д.М., Гридин А.М., Мишустин Б.А. Устройства СВЧ — М: Высш. школа,1981
4) Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория) — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III).
5) Сазонов Д. М.Антенны и устройства СВЧ. Учеб.для радиотехнически специальностей вузов. — М.: Высш. шк., 1988. — с. 432.