НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
Институт – Физико-технический
Направление (специальность) - физика
Кафедра – Общей физики
Отчет
По дисциплине: Компьютерные технологии в науке и образовании
По теме: “Программная реализация математической модели нестационарного теплопереноса в однородной пластине
Выполнил студент гр. 0БМ71 _____________ _________Кабдылкаков Е.А.
(Подпись) (Дата) И.О.Фамилия
Проверил ______________________________________________Е.А.Маслов
должность (Подпись) (Дата) И.О.Фамилия
:
Томск – 2017
Содержание
1 Условие задачи. 3
2 Физико-математическая постановка задачи. 3
3. Алгоритм численного решения. 5
4Тестовая проверка программы.. 7
5 Результаты решения задачи (1) – (4) 8
Выводы.. 10
Список литературы.. 10
Программный код на языке Pascal. 11
1Условиезадачи
Изоляционнаябадделитовая(ТУ14-8-248-77)пластинатолщиной L = 0,02 м, являющаяся элементом внутренней стенки плазмохимического реактора, имеет следующие теплофизические свойства: коэффициент теплопроводности λ = 1,2 Вт/(м·ºС), плотность ρ = 5100 кг/м3, теплоемкость Ср = 550 Дж/(кг·ºС). До запуска устройства пластина находилась при постоянной температуре T 0 = 20 ºС. В момент времени t = 0 на внутренней стороне температура стала равной T л = 2000 ºС, а с другой стороны температура всегда поддерживается постоянной Т п = 20 ºС. Определить температуру в центре пластины через 1 минуту.
2 Физико-математическая постановка задачи
Рассматриваетя бадделитовая пластина (см. рисунок 1), с одной стороны пластины прикладывается постоянная температура равной 2000 ºС. С другой стороны поддерживается постоянная температура. Определим температуру в центре пластины через 60секунд, при условии, что начальная температура пластины имела 20 ºС.При постановке задачи были приняты следующие допущения:
1. Вклад радиационной составляющей в теплообмен на внешней поверхности не учитывается.
2. Возможные процессы плавления и окисления материала преграды не рассматриваются.
3. Теплофизические характеристики (λ, ρ, с) пластины постоянны.

Рисунок 1. Область решения задачив Декартовой системе кодинат: L – длина пластины; Tл – температура внутренной стороны пластины; Tп – температура внешней стороны пластины.
Математическая модель, описывающая в рамках сформулированной задачи процесс прогрева КМ, включает одномерное уравнение теплопроводности (1) с соответствующими начальными (2) и граничными условиями (3), (4):
 𝑡> 0,0 <𝑥<𝐿
𝑡> 0,0 <𝑥<𝐿
| (1) |
Начальное условие:

| (2) |
Граничные условия:
Условие (II-рода) неограниченности пластины в направлении оси y:

| (3) |

| (4) |
где T – температура; t – время; ρ – плотность; с – коэффициент удельной теплоемкости; λ – коэффициент теплопроводности [1].
3. Алгоритм численного решения
Прирешениидифференциальногоуравнениявчастныхпроизводныхнаиболеечастоиспользуетсяметодконечныхразностей(МКР).Вместопроизводныхвдифференциальномуравнениииспользуютсяихконечно-разностныеаппроксимации.Припостроениидискретныхаппроксимацийкраевыхдифференциальныхзадачнужностремитьсяувязатьдве,возможно,противоречивыецели:хорошеекачествоаппроксимациииэффективноеустойчивоерешениеполучающихсяприэтомалгебраическихсистем.ПрииспользованииМКРдлязадачтеплопроводноститвердоетелопредставляютввидесовокупностиузлов.Заменяячастныепроизводныедифференциальногоуравнения(1)конечнымиразностямиполучаютсистемулинейныхалгебраическихуравненийдляопределениятемпературы,каклокальнойхарактеристикивкаждомузлесетки.Полученнаясистемаявляетсянезамкнутой,дляеезамыканияиспользуютразностноепредставлениеграничныхусловий.Врезультатеполучаютзамкнутуюсистемулинейныхалгебраическихуравнений,которуюрешаютчисленнымиметодамиспомощьюЭВМ [1].
Разобьёмпластинупотолщинена N равныхпромежутков,т.е.построимконечно-разностнуюсетку(рис.2).На рисунке 2 представлена, конечно-разностная сетка области решения

|
| Рисунок 2. Конечно-разностная сетка |
Определим значение температуры в i -ом узле в момент времени

| (5) |

| (6) |
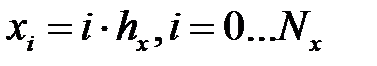
| (7) |

| (8) |
где τ–шаг интегрирования по времени; hx – шаг интегрирование по пространству; n – номер шага по времени; i – номер шага по пространству; Nx – количество шагов по длине; Nt – количество шагов по времени.
Далеезаменимдифференциальныеоператорыв(1)наихконечно-разностныеаналоги [2].Будемпользоватьсянеявнойсхемой:

| (9) |

| (10) |
Врезультатеаппроксимациичастныхпроизводныхсоответствующимиконечнымиразностямидифференциального уравнения (1) получимследующееразностное уравнение (11):


| (11) |
Для решение уравнение методом прогонки нужно привести уравнение (11) к следующему виду:
 . .
| (12) |
Перегруппируем слагаемые в уравнении (11) в порядке представленном в уравнении (12), а именно:


| (13) |
Тогда получимсоответствующие коэффициенты разностного шаблона (12):


| (14) |
4Тестовая проверка программы
В качестве примера применения метода конечных разностей (МКР) рассмотрим краевую задачу на основе одномерного уравнения теплопроводности (1) – (4). Анализируется теплопередача через плоскую бесконечную пластину или изолированный стержень (рис. 1). На одной границе пластины поддерживается постоянная температура TL = 300 °C, на другой границе - температура TR = 100 °C. Начальная температура равна T 0 = 20°C, источники тепловыделения внутри пластины отсутствуют.
Численное решение задачи (1) – (4) представлено на рисунке 3.

Рисунок 3. График изменения значенийтемпературы пластины по OX длятестовой задачи
Зелеными окружностями на рисунке 3 изображены данные полученные в работе [2] при решении задачи (1) – (4).Проведём сравнение результатов полученных численно с результатами работы [2] (см. таблицу 1).
Таблица 1. Значения температуры пластины в четырехточках по оси OX
| x, м | Tcalc, °С | Ttrue, °С | Δ, °С | Δ,% |
| 0,000 | 300,0000 | 300,0000 | 0,00001 | |
| 0,03 | 149,6390 | 150,0000 | -0,36140 | -0,241542 |
| 0,07 | 75,9014 | 76,0000 | -0,09860 | -0,1299318 |
| 0,10 | 100,0000 | 100,0000 | 0,00001 |
Погрешность расчета программы составляет менее 1%, что говорит о точности вычисление программы.
5Результатырешениязадачи (1) – (4)
Спомощью программыбылполученграфикраспределениятемпературыподлинепластинычерез10, 30, 50, 60 с (Рис.4).

Рисунок4.Графикизменениятемпературывцентре пластинепоосиОХ,через 10, 30, 50, 60 с
В таблице 2приведены результаты расчета значение температуры в середине пластины (см.таблица 2).
Таблица 2. Резлуьтаты вычисления температуры центра пластины
| t, c | Tcalc, oC |
| 10,0000 | 21,7136 |
| 30,0000 | 116,7535 |
| 50,0000 | 269,0813 |
| 60,0000 | 340,5201 |
Результаты расчета показывают, что температура в центре пластины увеличивается с увелечением времени. По результатам расчета температуры в центре пластины построен график изменения температуры от времени. На графике проведена линейная апроксимация (Рис. 5).

Рисунок 5. График изменения температуры в центре пластине по оси ОХ по времени
С увелечением времени, температура в центре пластины увеличивается линейно.
Выводы
С помощью метода конечных разностей было расчитано значение температуры в центре бадделитовой пластины в результате температурной разности двух сторон пластины в течении 60 секунд.
Была разработана программа на языке Pascal, в которой нестационарная уравнение теплопроводности решалось методом конечных разностей. Программа был протестирована на краевой задаче на основе одномерного уравнения теплопроводности. Результаты вычисление программы совпадали со значениеми на графика данной в задаче, что подтверждает точность вычисление программы.
С помощью расчета значений темпаратуры центра пластины через 10 с, 30 с, 50 с, 60 с было получена динамика изменения температуры в центре пластины по времени. С увелечением времени значение температуры в центре пластины увеличивалось. Был построен график изменения значение температуры для центра пластины от времени. Температура в центре пластины изменялось линейно, что подтвержадет линейная апроксимация графика.
Список литературы
1. Численные методы. Сборник задач: учеб. Пособие для вузов / В.Ю. Гидаспов, И.Э. Иванов, Д.Л. Ревизников и др.; под ред.У.Г. Пирумова. – М.: Дрофа, 2007. — 144 с.: ил.ISBN 978-5-358-01310-0
2. Кузнецов Г.В., Шеремет М.А. разностные методы решения задач теплопроводности: учебное пособие. / Г.В. Кузнецов, М.А. Шеремет. – М.:Томск: Изд-во ТПУ, 2007. — 172 с.
Программный код на языкеPascal.
Const
lamda=1.2;
ro=5100.0;
cp=550.0;
Lx= 0.02;
Nx= 100;
Time=60;
Nt=60;
T0=20;
Tl=2000;
Tr=20;
type vec= array [0..Nx] of real;
var ai, bi, ci, di, Ti: vec;
i: integer; txt: text;
hx, tau, t, z: real;
procedure TDMA(N:integer; a, b, c, d: vec; var x: vec);
var i: integer; z: real;
P, Q: vec;
Begin
P[0]:= -c[0]/b[0]; Q[0]:=d[0]/b[0];
for i:=1 to N do begin
z:=a[i]*P[i - 1]+b[i];
P[i]:= - c[i]/z;Q[i]:=(d[i] - a[i]*Q[i - 1])/z;
end;
x[N]:=Q[N];
for i:=N - 1 downto 0 do
x[i]:=P[i]*x[i+1]+Q[i];
End;
BEGIN
hx:=Nx; tau:=Nt;
hx:=Lx/hx; tau:=Time/Nt;
for i:= 0 to Nx do
Ti[i]:= T0;
ai[0]:=0.0; bi[0]:=1.0; ci[0]:=0.0; di[0]:=TL;
ai[Nx]:=0.0; bi[Nx]:=1.0; ci[Nx]:=0.0; di[Nx]:=TR;
z:=hx*hx;
for i:=1 to Nx-1 do begin
ai[i]:=-lamda/z;
bi[i]:=2.0*lamda/z+ro*cp/tau;
ci[i]:=-lamda/z;
end;
z:=ro*cp/tau;
t:=0;
While (t<Time) do Begin
t:=t+tau;
for i:=1 to Nx-1 do
di[i]:=z*Ti[i];
TDMA(Nx,ai,bi,ci,di,Ti);
End;
Assign(txt,'T(x).txt');
Rewrite(txt);
for i:=0 to Nx do
writeln(txt,' ',hx*i:16:5,' ',Ti[i]:16:5);
close(txt);
End.