Тема занятия: Расстояние до звёзд. Пространственные скорости звёзд.
ЗАДАНИЕ:
Прочитать материал учебника Воронцов-Вельяминов. Астрономия 11: с.143-147, 150, 184-185
Написать конспект по материалу в этом документе.
Подготовиться к проверочной работе по двум занятиям: «Общие сведения о Солнце. Солнце и жизнь Земли» и «Расстояние до звёзд. Пространственные скорости звёзд»
РАССТОЯНИЯ ДО ЗВЁЗД
Не только в геоцентрических, но и в гелиоцентрической системе мира существовало представление о «сфере неподвижных звёзд». Считалось, что звёзды расположены на шаровой поверхности, т. е. все они отстоят от нас на одном и том же расстоянии и не движутся относительно друг друга. Эти представления ошибочны..
1. Определение расстояний до звёзд. Вы знаете, что при измерении расстояний до тел Солнечной системы применяется метод горизонтального параллакса. Он пригоден и для определения расстояний до ближайших звёзд. Только в качестве базиса используется не радиус Земли, а средний радиус земной орбиты.
ОПР. Угол π, под которым со звезды был бы виден средний радиус а земной орбиты, расположенный перпендикулярно направлению на звезду, называется годичным параллаксом (рис. 1). В тех случаях, когда удаётся определить значение π, расстояние r до звезды вычисляется по формуле r = 
(1)
Угол 𝜋 всегда очень мал (меньше 1"). Поэтому формулу (1) можно записать в виде
r = 
(2)
ОПР. Расстояние до звезды, которое соответствует параллаксу в 1", называется парсеком (от слов «параллакс» и «секунда»; обозначается пк):
1 пк = 206 265 а. е.
| Рис.1. Годичный параллакс |
Очевидно, что расстояние до звезды в парсеках легко вычислить по формуле
(3)
Самая близкая к нам звезда (не считая Солнца!) находится в созвездии Центавра (Проксима Центавра или Кентавра) на расстоянии 1,3 пк, или 270 000 а. е.; её годичный параллакс составляет 0,77". Полтора века назад астрономам, в том числе астроному Пулковской обсерватории В. Я. Струве (1793—1864), удалось впервые определить расстояние до звезды Вега (7,8 пк). Сейчас уже известны параллаксы нескольких тысяч звёзд.
Выясним, сколько километров содержится в парсеке, а также найдём соотношение между парсеком и световым годом — расстоянием, которое свет проходит за год (обозначается св. год, св. лет).
Поскольку 1 а. е. = 1,496 ∙ 108 км, то
1 пк = 206 265 а. е. = 206 265 ∙ 1,496 ∙ 108 км = 3,08 ∙ 1013 км;
1 св. г. = 3 ∙ 105 км/с ∙ 365,25 ∙ 24 ∙ 3600 с = 9,46 ∙ 1012 км;
1 пк=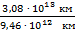 
св.лет = 3,26 св. года;
103 пк = 1 кпк (килопарсек); 106 пк = 1 Мпк (мегапарсек).
Задача 1. Годичный параллакс Веги (α Лиры) равен 0,12". Каково расстояние до неё в парсеках и световых годах?
| Дано: π =0,12" r пк -? r св.лет -? | Решение: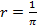 
 пк = 8,33 пк;
r св.лет = 3,26 св.г∙8,33=27,1 св.года.
|
Ответ: r пк = 8,33 пк; r св.лет = 27,1 св.года.
2. Видимые и абсолютные звёздные величины. Уже из первого знакомства со звёздным небом вы знаете о том, что яркость звёзд неодинакова. Со времён древнегреческого астронома Гиппарха (II в. до н. э.) используется понятие «звёздная величина». Считая, что расстояния до звёзд одинаковы, предполагали, что чем звезда ярче, тем она больше. Наиболее яркие звёзды отнесли к звёздам первой величины (сокращённое обозначение 1m, от лат. magnitudo — величина), а едва различимые невооружённым глазом — к шестой (6m). Сейчас мы знаем, что звёздная величина характеризует не размеры звезды, а её блеск, т. е. освещённость, которую создаёт звезда на Земле.
Но шкала звёздных величин сохранилась. Блеск звезды 1m больше блеска звезды 6m ровно в 100 раз. Следовательно, разность в 5 звёздных величин соответствует различию в блеске ровно в 100 раз. Обозначим через х число, показывающее различие в блеске в одну звёздную величину, тогда х 5 = 100.
Найдём значение х из этого уравнения:
5 lg х = lg 100, откуда 5 lg х = 2, или lg х = 0,4, тогда х = 2,512.
Если обозначить блеск звезды, звёздная величина которой равна m1, через I1, а блеск звезды, звёздная величина которой равна m2, через I2, то
(4)
Светила, блеск которых превосходит блеск звёзд 1m, имеют нулевые и отрицательные звёздные величины (0m, −1m и т. д.). К ним относятся несколько наиболее ярких звёзд и планет, а также, конечно, Солнце и Луна. Шкала звёздных величин продолжается и в сторону звёзд, не видимых невооружённым глазом. Есть звёзды 7m, 8m и т. д. Для более точной оценки блеска звёзд используются дробные звёздные величины: 2,Зm; 7,1m; 6,2m; 14,5m и т. д.
Задача. Во сколько раз Капелла ярче Денеба?
Из таблицы (см. Приложение) найдём звёздную величину Капеллы (m1 = +0,2m) и Денеба (m2 =+1,Зm).
Решение: Запишем основную формулу
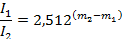
Прологарифмируем:
- = (m2 – m1) lg 2,512,
а так как lg 2,512 = 0,4,
то для Капеллы и Денеба
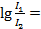0,4 ∙ 1,1 = 0,44; 
= 2,75.
Ответ: = 2,75.
Так как звёзды находятся от нас на различных расстояниях, то их видимые звёздные величины ничего не говорят о светимостях (мощности излучения) звёзд. Поэтому в астрономии, кроме понятия «видимая звёздная величина», используется понятие «абсолютная звёздная величина».
Звёздные величины, которые имели бы звёзды, если бы они находились на одинаковом расстоянии (r 0 = 10 пк), называются абсолютными звёздными величинами (М).
Пусть какая-нибудь звезда удалена от нас на расстояние r. Обозначим её видимую звёздную величину через m, абсолютную — через М. Воспользовавшись формулой (4), запишем:
где I и I 0 — блеск звезды (точнее, создаваемая ею на Земле освещённость) на расстояниях r и r 0 = 10 пк. Поскольку освещённость изменяется обратно пропорционально квадрату расстояния, то 
или 
Поэтому 
Отсюда, логарифмируя, найдём:
2 − 2lg r = 0,4(М− m), или М− m = 5− 5 lg r
Тогда М = m + 5− 5 lg r (5)
По формуле (5) можно вычислить абсолютную звёздную величину, если известны видимая звёздная величина и расстояние до звезды. Абсолютная звёздная величина Солнца M⨀ = +4,8 m.
Если абсолютная звёздная величина звезды определена другим способом, например по спектру звезды, то из формулы (5) можно найти расстояние до звезды:
=0,2(m − М) +1 (6).
Вопросы и задания для самоконтроля
1. Что используется в качестве базиса при определении годичных параллаксов звёзд? Почему? 2. Какие единицы применяются при измерении расстояния до звёзд? Каково соотношение между этими единицами? 3. Какие два метода определения расстояний до звёзд вы знаете?
ПРОСТРАНСТВЕННЫЕ СКОРОСТИ ЗВЁЗД
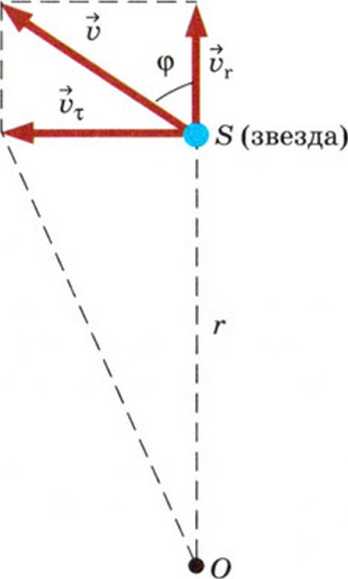
Введение. Итак, звёзды находятся от нас на различных расстояниях, т. е. никакой «сферы звёзд» не существует. По не существует и неподвижных звёзд. Астрономические наблюдения доказывают, что звёзды движутся. Скорость, с которой звезда движется в пространстве относительно Солнца, назовём пространственной скоростью. Обозначим вектор пространственной скорости одной из звёзд через 
(рис. 2). Его можно представить как сумму двух составляющих векторов, один из которых (тангенциальная скорость 
) перпендикулярен лучу зрения (т. е. направлению звезда — наблюдатель), а другой направлен по лучу зрения (лучевая скорость 
.). Тогда по теореме Пифагора модуль пространственной скорости будет равен
(7)
(наблюдатель)
Рис.2. Пространственная скорость звезды
|
и .
10. Собственные движения и тангенциальные скорости звёзд. Уже в XVIII в. стало ясно, что экваториальные координаты звёзд в течение длительных промежутков времени изменяются. Одна из причин этого явления — движение звёзд в пространстве. Угловое перемещение звезды на небесной сфере за год называется собственным движением. Оно выражается в секундах дуги в год и обозначается буквой μ. Наибольшим собственным движением обладает звезда Барнарда (в созвездии Змееносца), у которой μ = 10,3". Зная μ, можно вычислить модуль тангенциальной скорости 𝑣𝜏. Действительно, расстоянию r до звезды соответствует годичный параллакс звезды π. Если π выражено в радианах, то r = а /π где а = 1 а. е. Собственному движению звезды μ (тоже выраженному в радианах) соответствует линейное смещение rμ Учитывая сказанное выше, r μ = а 
. Зная перемещение звезды за год, легко найти её скорость 𝑣𝜏, разделив это перемещение на время t0, равное году:
𝑣𝜏 = а 
Так как 1 а. е. = 1,496 ∙ 108 км, a t0 = 3,16 ∙ 107 с, то тангенциальная скорость, выраженная в километрах в секунду, будет
𝑣𝜏 = 4,74∙ -. (8)