Аксиоматика и доказательство формул
Система логических аксиом логики первого порядка состоит из аксиом исчисления высказываний дополненной двумя новыми аксиомами:
и 
,
где 
— формула, полученная в результате подстановки терма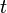 
вместо каждой свободной переменной 
, встречающейся в формуле 
.
Правил вывода 2:
· Modusponens:Правило обобщения (англ.):
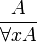
Свойства
· полнота (это означает, что для любой замкнутой формулы выводима либо она сама, либо её отрицание);
· непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием).
Использование
Возьмем рассуждение «Каждый человек смертен. Конфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» черезЧЕЛОВЕК(x) и «x смертен» через СМЕРТЕН(x). Тогда утверждение «каждый человек смертен» может быть представлено формулой: 
x(ЧЕЛОВЕК(x) →СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой
( x(ЧЕЛОВЕК(x) →СМЕРТЕН(x)) 
ЧЕЛОВЕК(Конфуций)) →СМЕРТЕН(Конфуций)
Пример 1 Доказать, что формула 
общезначима
1) {FA,TB,FC,FA,FB} – замкнутая;
2) {FA,TB,FC,TA} – замкнутая;
3) {FA,TB,FC,TC} – замкнутая;
4) {TA,TA,FA,FC} – замкнутая;
5) {TA,TB,FA,FC} – замкнутая;
6) {FB,TA,FA,FC} – замкнутая;
7) {TC,TA,FA,FC} – замкнутая;
8) {FB,TB,FA,FC} – замкнутая;
9) {TC,TB,FA,FC} – замкнутая.
Все таблицы замкнутые, значит, формула является общезначимой.Если при исследовании формул наобщезначимость, итоговые таблицы этой формулы с индексом F все замкнуты, то она являетсяобщезначимой. Аналогично, если формула исследуется с индексом Т и все итоговые таблицы замкнуты, то она являетсяпротиворечием.В противном случае формула являетсянейтральной.
Пример2 Установить, является ли формула 
общезначимой.
Выпишем итоговые таблицы:
1){TA,FB,TA,FB} незамкнутая;
2){TA,FB,FA,TB} замкнутая;
3){FB,TA,FB} незамкнутая;
4){TA,TA,FB} незамкнутая;
5){FA,FA,TB} замкнутая;
6){TA,FB,TB} замкнутая.
Среди итоговых таблиц есть незамкнутые, следовательно, формула не является общезначимой.
Если все итоговые таблицы формулы с индексом F-замкнуты, то формула является общезначимой.
11. Выразить на языке модальной (временной, эпистемической) логики логическую структуру данного высказывания.
12. Построить модель для указанной формулы (модальной, эпистемической, темпоральной) логики.
13. Привести пример высказывания, которое бы выполнялось в данной модели (модальная, темпоральная, эпистемическая логика).
14. Описать результат информационного обновления.
15. Формализовать решение задачи средствами динамической эпистемической логики (по типу задач о «чумазых детях»).
Билет 1. Предмет логики. Понятия логической формы, логического следования, логического закона. Логика традиционная и математическая.
Логика – это теория правильных рассуждений. Является одной из древнейших наук. Как стройная система знаний она сформировалась в IVв. до н. э. в трудах Аристотеля. Логика исследует логические формы, отвлекаясь от их конкретного содержания, анализирует мышление со стороны его формальной правильности.
Предметом логики является знание, полученное из ранее проверенных истин в соответствии с определенными законами. Ее задача заключается в том, чтобы установить, следует ли вывод из определенных посылок с необходимостью либо вероятно. Другой задачей является формализация и систематизация правильных способов рассуждений.
Формальная логика представлена сегодня двумя науками - традиционной и математической (символической) логикой.
Традиционная логика - это первая ступень логики выводного знания. Она изучает общечеловеческие формы мысли (понятия, суждения), формы связи мыслей в рассуждении (умозаключения), зафиксированные в системе формально-логических законов (тождества, противоречия, исключенного третьего и достаточного основания).
Математическая логика - вторая после традиционной логики ступень в развитии формальной логики, применяющая математические методы и специальный аппарат символов и исследующая мышление с помощью исчислений (формализованных языков). Большая, чем в традиционной логике, степень абстрагирования и обобщения позволяет современной символической логике познавать новые закономерности мышления, возникающие при решении сложных логических конструкций в математике, кибернетике.
Логическая форма – это структура мысли или способ связи элементов ее содержания. Выражения, истинные в силу своей логической формы, называют логически истинными. Отсюда следует понятие логического закона.
Логическое следование – отношение между высказываниями по форме.
Логический закон – это такая логическая форма, которая принимает значение «истина» при любой интерпретации параметров, входящих в ее состав.
Билет 2. Язык как информационная знаковая система. Синтаксис, семантика, прагматика. Принципы построения формализованных логических языков.
Язык – это знаковая система, предназначенная для фиксации, переработки и передачи информации от одного субъекта к другому. Языки подразделяются на естественные и искусственные.
Формализованный язык логики – искусственный язык логики, предназначенный для воспроизведения логических форм контекстов естественного языка, а также выражения логических законов и способов правильных рассуждений в логических теориях, строящихся в данном языке.
Построение формализованного языка начинается с задания его алфавита – совокупности исходных, примитивных символов. В алфавит включаются логические символы, нелогические символы и технические символы. Задаются различные типы правильно построенных выражений, формулы.
Включают так называемые правила преобразования – процедуры дедукции, точные правила переходов от одних последовательностей символов к другим. В этом случае формализованный язык, по существу, отождествляется с логическим исчислением.
Языки силлогистики позволяют фиксировать логические формы атрибутивных высказываний.
Синтаксис интересуется поведением знаков в составе языка как некоторых материальных объектов, отвлекается от наличия интерпретатора и от того, что знак обозначает. Исследуются отношения знаков друг к другу: способы их комбинирования, образования из них языковых конструкций, преобразования одних знаковых комбинаций в другие.
Семантика исследует отношения между знаками и обозначаемыми объектами, т. е. знаки и смыслы знаков. Выделяются различные категории знаков в зависимости от типов их значений, а также от типов выражаемых этими знаками смыслов.
Прагматический анализ языка состоит в исследовании отношений между знаками и интерпретаторами, использующими эти знаки. При таком подходе решается важная задача – установление зависимости значения и смысла знака от тех или иных особенностей интерпретатора и внеязыкового контекста, сопутствующего употреблению данного знака.
Билет 3. Традиционная силлогистика: способ анализа и условия истинности простых категорических суждений. Распределенность терминов в простых категорических суждениях. Традиционная силлогистика и логика предикатов.
Силлогистика – это теория выводов из простых категорических суждений. (Аристотедь, схоласты). Силлoгизмы подразделяются нa coвepшeнные (зaключeниe c лoгичecкoй нeoбxoдимocтью cлeдyeт из eгo пocылoк по пpинципy: «Ecли X, тo Y; ecли Y, тo Z; cлeдoвaтeльнo, ecли X, тo Z»)и нecoвepшeнные (прабавляютк имeющимcя пocылкaм дoп. пocылкy, либo пpoизводят дoп. преобразования, чтобы стать совершенным).
Традиционная силлогистика рассматривает единичное по аналогии с общим.
Способ анализа и условия истинности простых категорических суждений – см. с 246 – 249 (Бочаров, Маркин).
Простой кaтeгopичecкий cиллoгизм (cиллoгизм) - этo дeдyктивнoe yмoзaключeниe, в кoтopoм из двyx кaтeгopичecкиx выcкaзывaний вывoдитcя нoвoe кaтeгopичecкoe выcкaзывaниe.
Простые категорические суждения (пропозиции):
1. Атрибутивные (о свойствах)
2. Реляционные (об отношениях)
3. Экзистенциальные (о существовании)
Выpaжeния «Bce... ecть...», «Heкoтopыe… ecть...» и т.д. - лoгичecкиe пocтoянныe, mеpмuнaмы cuллoгuзмa. Пpимep: Все М есть Р. Все S есть М. Все S есть Р.
Bce жидкocти yпpyги.
Boдa – жидкocть.
Boдa yпpyгa.
В кaждoм cиллoгизмe дoлжнo быть тpи тepминa: мньший, бльший и cpeдний. Mеньшим mepмuнoм нaзывaeтcя cyбъeкт зaключeния («вoдa»S). Бльший - пpeдикaт зaключeния («yпpyгa»P). Tepмин, пpиcyтcтвyющий в пocылкax, нo oтcyтcтвyющий в зaключeнии -средний («жидкость»M).
Логические константы (союзы) определяют виды сложных суждений и обозначаются специальными символами:
- конъюнкция " и " образует соединительное суждение (а Ù b);
- дизъюнкция " или " образует разделительное суждение (а v b);
- строгая дизъюнкция " либо " образует исключающе-разделительное суждение (а Ú b);
- импликация " если..., то " (
) образует условное суждение (а b);
- эквиваленция " тогда и только тогда, когда " 
- сокращённая запись 
;
- отрицание " неверно, что " образует отрицательное сложное суждение (ā) или (a).
Также см.: https://iph.ras.ru/uplfile/logic/log17/Li_17_Ilyin.pdf
В суждениях S и Р могут распределены (если объем термина полностью включается в объем другого термина или полностью исключается из него) не распределены (если объем термина частично включается в объем другого термина или частично исключается из него).
Также см.: https://allrefs.net/c12/470de/p28/
Предикат – повествовательное предложение, содержащее предметные переменные, определенные на соответствующих множествах. При замене переменных конкретными значениями (элементами этих множеств) предложение обращается в высказывание, т.е. принимает значение «истина» или «ложь».
Язык логики предикатов - это система символов, создающие алфавит К нему относятся символы, введенные в логике высказываний, и новые символы, обозначающие сроки, введены в логике предикатов
Непосредственные силлогистические умозаключения. Выводы по логическому квадрату.
Непосредственные умозаключения делятся на следующие типы: превращение, обращение, противопоставление предикату и умозаключение по логическому квадрату.
«a» - общеутвердительное, SaP;обращается в PaS, PiS
«e» - общеотрицательное, SeP; обращается в PeS
«i» - частноутвердительное, SiP; обращается в PiS
«o» - частноотрицательное, SoP; не обращается.
Логический квадрат служит мнемоническим целям, способствуя запоминанию логических отношений между высказываниями с одинаковыми субъектами и предикатами
Это отношения подчинения, когда из одного высказывания логически следует другое (Всякий Sесть P=>Некоторый Sесть P). Отношение подчинения имеет место между высказываниями aи I (a =>i), eи o (e =>o).
Это отношение контрарности между высказываниями типа aи e (они не могут быть одновременно истинными, но могут быть одновременно ложными). Существует закон контрарного противоречия.
Это отношение субконтрарности между Iи o, которые могут быть одновременно истинными, но не могут быть одновременно ложными. Отсюда закон субконтрарного третьего.
Отношения контрадиторности или противоречия, расположенные по диагоналям квадрата. Это означает, что высказывания не могут быть одновременно истинными и одновременно ложными. Существуют:
1. Закон противоречия для a и o
2. Закон противоречия для e и I
3. Закон исключенного третьего для a и o
4. Закон исключенного третьего для e и I
Превращение – вид непосредственного умозаключения, при котором изменяется качество посылки без изменения её количества, при этом предикат заключения является отрицанием предиката посылки.
Обращение – непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения, т.е. в заключении субъектом является предикат, а предикатом – субъект исходного суждения. Подчиняется правилу распределённости терминов в суждении. Различают простое (чистое)(если субъект и предикат исходного суждения или оба распределены, или оба не распределены) обращение и обращение с ограничением (исходном суждении субъект распределён, а предикат не распределён или, наоборот, субъект не распределён, а предикат распределён).
Операция противопоставления предикату – последовательное применение к исходному высказыванию операции превращения и к полученному результату – обращения. Операция противопоставления предикату не выполняется для высказываний I.
Операция противопоставления субъекту выполняется наоборот (обращение ->превращение).
Для того, чтобы сделать умозаключения по логическому квадрату, необходимо:
1. Определить тип суждения-посылки и значение его истинности
2. Сформулировать три другие типы суждений с теми же S и Р и определить значение истинности полученных суждений-выводов
3. Проверить соответствие их значений истинности при установке четырех типов отношений между суждениями
Например, пусть дана истинная посылка А: «Все войны есть продолжение политики». Из нее следуют выводы:
1) Е - «Ни одна война не является продолжением политики» - ложный;
2) I - «Некоторые войны являются продолжением политики» - истинный;
3) О - «Некоторые войны не являются продолжением политики» - ложный.
Смысл умозаключений по логическому квадрату состоит в том, что знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.
См. https://edu.dvgups.ru/METDOC/CGU/FILOSOF/LOGIKA/METOD/MOTOVNIK/IV.htm
Билет 5. Простой категорический силлогизм, его состав, фигуры и модусы. Общие правила силлогизма. Проверка силлогизмов с использованием круговых диаграмм.
Простой категорический силлогизм - такое умозаключение, в котором заключение и посылки являются простыми категорическими суждениями. Категорические суждения - такие, в которых мысль утверждается или отрицается вполне определенно, без всяких условий, и которые имеют субъектно-предикатную структуру.
Пример:
Все кошки ловкие.
Маруся – кошка.
Маруся ловкая.
Структура силлогизма:
· Понятия, входящие в состав силлогизма, называются терминами силлогизма.
· Меньший термин – это субъект заключения. Его содержит меньшая посылка.
· Больший термин – предикат заключения. Его содержит большая посылка.
· Общий для обеих посылок термин – средний термин.
В примере:
Кошка – средний термин, М. Общий
Ловкий – больший термин, Р. предикат заключения
Маруся – меньший термин, S. субъект заключения
Все М есть Р.
Sесть M.
S есть P.
· Модусы, для которых между посылками и заключением существует отношение логического следования, называются правильными. Всего существует 24 правильных модуса. (см. табл. 3 с. 257, Бочаров, Маркин)
Существуют общие правила силлогизма. Они включают в себя правила посылок и правила терминов. А именно:
· Для терминов:
1. Средний термин должен быть распределен хотя бы в одной из посылок.
2. Если крайний термин не распределен в посылке, то он не должен быть распределен в заключении.
· Для посылок:
1. По крайней мере одна из посылок должна быть утвердительной.
2. Если обе посылки утвердительные, то заключение тоже должно быть утвердительным.
3. Если имеется отрицательная посылка, то и заключение должно быть отрицательным.
Чтобы проверить правильность рассуждения, можно использовать круговые схемы, на которых все посылки одновременно принимают значение истины.
Категорический силлогизм – вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, связанных средним термином, при соблюдении правил вывода необходимо следует заключение.
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В простом категорическом силлогизме только 3 термина:
Фигурами категорического силлогизма называются формы силлогизма, различающиеся по положению среднего термина (М) в посылках. Имеется четыре фигуры категорического силлогизма:
https://edu.dvgups.ru/METDOC/CGU/FILOSOF/LOGIKA/METOD/MOTOVNIK/IV.htm
Билет 6. Сокращенный силлогизм (энтимема).
При осуществлении определенного аргументационного процесса, обычно пользуются не развернутой формой силлогизма, а используют так называемые энтимемы.
Энтимема – это сокращенная форма рассуждения с пропуском некоторых посылок и заключения.
Энтимемы бывают корректными и некорректными. Энтимема считается корректной, если выполнено два условия:
1. Она может быть восстановлена до правильного модуса категорического силлогизма.
2. Все посылки в восстановленном правильном модусе оказываются истинными утверждениями.
Согласно теории аргументации, аргументация корректна только тогда, когда все аргументы истинны.
Проверка правильности энтимемы: см. с. 261 – 263, Бочаров, Маркин.
Силлогизм с пропущенной посылкой или заключением называется сокращённым силлогизмом или энтимемой. "энтимема" с греческого означает "в уме".
Использование энтимем обусловлено тем, что пропущенная часть силлогизма или содержит известное положение, которое не нуждается в устном или письменном выражении, или в контексте выраженных частей умозаключения она легко подразумевается.
Пример: "Воробьёв – гимназист, поэтому он обязан посещать занятия". Здесь пропущена большая посылка – "Все гимназисты обязаны посещать занятия". Так как она представляет собой общеизвестное положение, то формулировать эту посылку не обязательно. Пропущены могут быть и меньшая посылка, и заключение. "Все гимназисты обязаны посещать занятия, значит, и Воробьёв обязан посещать занятия" – пропущена меньшая посылка, или: "Все гимназисты обязаны посещать занятия, а Николаев – гимназист" – пропущено заключение. Пропущенные части подразумеваются.
Поскольку в энтимеме выражены не все части умозаключения, возможную скрывающуюся ошибку обнаружить труднее, чем в полном силлогизме. Для проверки правильности рассуждения следует найти пропущенные части умозаключения и восстановить энтимему в полный силлогизм.
Сложные и сложносокращённые силлогизмы (сориты)
Сложным силлогизмом называются два или несколько простых категорических силлогизмов, связанных друг с другом так, что заключение одного из них становится посылкой другого.
Различают прогрессивные и регрессивные полисиллогизмы.
В ходе рассуждения полисиллогизм принимает обычно сокращённую форму. Полисиллогизм, в котором пропущены некоторые посылки, называется соритом (от греческого "куча"). Различают два вида соритов:
1. Прогрессивный 2. Регрессивный сорит
К сложносокращённым полисиллогизмам относится также эпихейрема ("нападение"). Эпихейремой называется сложносокращённый полисиллогизм, посылками которого являются энтимемы.
Энтимема 1: Распространение заведомо ложных, позорящих другое лицо измышлений уголовно наказуемо, т. к. является клеветой.
Энтимема 2: Действия обвиняемого представляют собой распространение заведомо ложных, позорящих другое лицо измышлений, т. к. они выразились в умышленном извращении фактов в заявлении на гражданина Н.
Развернём посылки эпихейремы в полные силлогизмы.
Билет 7. Язык классической логики высказываний. Табличное построение классической логики высказываний. Сокращенные таблицы истинности.
Логика высказываний (пропозициональная логика) – это логическая теория, язык которой содержит один тип нелогических символов – пропозициональные переменные, а также один тип логических символов – пропозициональные связки.
Классическая логика высказываний является наиболее простой логической теорией. Она абстрагируется от содержаний простых высказываний и их внутренней структуры, а учитываются лишь связки между ними и порядок их сочленения в сложные. Особенности ее языка определяют специфику ее законови то, в каких случаях из множества формул логически следует некоторая формула.
Законами классической пропозициональной логики являются формы высказываний, логическая истинность которых обусловлена логическими свойствами содержащихся в них пропозициональных связок.
↓ - «ни, ни»
Язык классической логики предикатов состоит из нелогических (пропорциональные переменные), логических (истинностно-истинностные пропозициональные связки) и технических символов.
Чтобы придать точное значение логическим символам алфавита, нужно сопоставить ей определенную функцию истинности. Это чаще всего делается с помощью таблиц истинности.
Количество высказываний (столбцов) в таблице - степень, в которую нужно возвести 2, чтобы получить количество строк.
Построение таких таблиц осуществляется следующим образом:
1. Выделяются все различные пропозициональные переменные, входящие в состав формулы.
2. В столбик выписываются все возможные наборы значений переменных.
3. В составе формулы выделяются все подформулы (начиная от элементарных и заканчивая самой формулой).
4. Вычисляется значение каждой подформулы при каждом наборе значений переменных.
Таблицы истинности можно создавать в сокращенной форме: отдельно выписываются лишь элементарные подформулы, значения сложных подформул указываются под их главными знаками в составе основной формулы, а непосредственно значение самой формулы указывается под ее главным знаком. (см. с. 97, Бочаров, Маркин).
Билет 8. Выполнимость, тождественная истинность и тождественная ложность высказываний. Логическая, аналитическая и априорная истинность.
Используя метод построения таблиц истинности, можно решать вопрос о том, является ли какая-либо формула языка классической пропозициональной логики законом этой теории.
Законом классической логики высказываний является формула, принимающая значение истины при любых наборах значений входящих в нее пропозициональных переменных. Формулы данного типа называются тождественно-истинными или общезначимыми. В результирующем столбце таблицы в каждой строке получаем истину.
Выделяют еще три класса формул:
· Формула называется тождественно-ложной, если и только если она принимает значение «ложь» при любых наборах значений входящих в нее пропозициональных переменных.
· Формула выполнима тогда и только тогда, когда она принимает значение «истина» по крайней мере при одном наборе значений входящих в нее пропозициональных переменных. К ним относятся все общезначимые формулы.
· Формула опровержима, если и только если она принимает значение ложь по крайней мере при одном наборе значений входящих в нее пропозициональных переменных. К ним относятся все тождественно-ложные формулы.
Истинность многих положений математики и логики напрямую связана с принятыми соглашениями об употреблении терминов (конвенциями). Они позволяют устанавливать истинность предложений априорно, т. е. не обращаясь к эмпирическому опыту. Для логики высказываний процедурой установления априорной истинности является построение таблиц истинности. К предложениям указанного типа могут применять иную терминологию. Например, их называют аналитически истинными (для предложений логики говорят об их логической истинности).
Билет 9. Способы установления отношений между высказываниями и проверка правильности рассуждений по истинностным таблицам.
Логические отношения между высказываниями бывают фундаментальными и производными.
· Фундаментальные отношения:
1. Совместимость по истинности:
Формулы множества Г называются совместимыми по истинности в некоторой логической теории Т, если и только если в Т существует интерпретация нелогических символов, входящих в указанные формулы, при которой каждая формула, входящая в Г, принимает значение истина. В противном случае эти формулы несовместимы по истинности.
2. Совместимость по ложности:
Формулы из множества Г называются совместимыми по ложности в теореме Т, если и только если в Т существует интерпретация нелогических символов, входящих в указанные формулы, при которой каждая формула из Г принимает значение «ложь». В противном случае эти формулы несовместимы по ложности.
3. Логическое следование:
Из множества формул Г логически следует формула B в некоторой логической теории Т, если и только если в Т не существует интерпретации нелогических символов, входящих в Г и В, при которой каждая формула из Г принимает значение «истина», а формула В – значение «ложь». В противном случае формула В не следует из Г.
Практически эти отношения можно установить с помощью таблиц истинности. Необходимо построить для этих формул совместную таблицу истинности и проверить на ней отношения между формулами.
Алгоритм построения:
1. Выделяют различные пропозициональные переменные, которые входят в состав формул.
2. Задают все возможные наборы их значений.
3. Вычисляют значения каждой из формул на каждом из заданных наборов.
· Производные отношения.
Они определяются на основе фундаментальных отношений. Наиболее употребимые:
1. Отношение противоречия (контрадикторности):
Если и только если они несовместимы по истинности и несовместимы по ложности.
2. Отношение противоположности (контрарности):
Тогда и только тогда, когда они несовместимы по истинности, но совместимы по ложности.
3. Отношение логической эквивалентности:
Если из А следует Б, а из Б следует А.
4. Отношение логического подчинения:
А логически подчиняется Б, если из Б следует А, но из А не следует Б.
5. Отношение логической независимости:
Формулы А и Б логически независимы, если и только если они совместимы по истинности и по ложности и не следуют друг из друга.
Метод таблиц истинности позволяет проверить умозаключения, осуществляемые на естественном языке, средствами классической логики высказываний. Для этого необходимо:
1. Выразить в языке клв логическую форму его посылок и заключения.
2. Построить совместную таблицу истинности.
3. Ответить на вопрос, следует ли логическая форма заключения из логических форм посылок.
4. Умозаключение правильно, если имеет место логическое следование.
Также с помощью таблиц истинности можно устанавливать отношения между высказываниями естественного языка.