Область применения
Данный метод обработки статистических данных широко применяется в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
· Гмурман В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с.
· Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с.
· Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с..
Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд методов.
1  . Графический метод, когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии. Анализируя эту линию, визуально можно определить характер зависимости между признаками x и y. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции.
. Графический метод, когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии. Анализируя эту линию, визуально можно определить характер зависимости между признаками x и y. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции.

4. Линейный коэффициент корреляции применяется в случае линейной зависимости между двумя количественными признаками x и y. В линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:
Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у:
Для измерения тесноты связи между x и y используется линейный коэффициент корреляции:
 ,
,
где xi, yi –индивидуальные значения факторного и результативного признаков;
 ,
,  – средние значения факторного и результативного признаков;
– средние значения факторного и результативного признаков;
 ,
,  – средние квадратические отклонения по факторному и результативному признакам;
– средние квадратические отклонения по факторному и результативному признакам;
n – объём совокупности.
Для расчёта линейного коэффициента корреляции воспользуемся вспомогательной таблицей. - пример:
| № | 
| 
| 
| 
| 
| 
| 
|
| -4,1 | -4,4 | 18,04 | 16,81 | 19,36 | |||
| 6,1 | -4 | -3,4 | 13,6 | 11,56 | |||
| 6,8 | -3,3 | -0,4 | 1,32 | 10,89 | 0,16 | ||
| 7,2 | -2,9 | -2,4 | 6,96 | 8,41 | 5,76 | ||
| 7,4 | -2,7 | -4,4 | 11,88 | 7,29 | 19,36 | ||
| 7,9 | -2,2 | -3,4 | 7,48 | 4,84 | 11,56 | ||
| 8,2 | -1,9 | -2,4 | 4,56 | 3,61 | 5,76 | ||
| 8,5 | -1,6 | -1,4 | 2,24 | 2,56 | 1,96 | ||
| 8,9 | -1,2 | -0,4 | 0,48 | 1,44 | 0,16 | ||
| 9,1 | -1 | 1,6 | -1,6 | 2,56 | |||
| 9,4 | -0,7 | -1,4 | 0,98 | 0,49 | 1,96 | ||
| 9,9 | -0,2 | 0,6 | -0,12 | 0,04 | 0,36 | ||
| 10,5 | 0,4 | 0,6 | 0,24 | 0,16 | 0,36 | ||
| 11,2 | 1,1 | 1,6 | 1,76 | 1,21 | 2,56 | ||
| 11,3 | 1,2 | -0,4 | -0,48 | 1,44 | 0,16 | ||
| 11,5 | 1,4 | 2,6 | 3,64 | 1,96 | 6,76 | ||
| 11,7 | 1,6 | 2,6 | 4,16 | 2,56 | 6,76 | ||
| 12,1 | 1,6 | 3,2 | 2,56 | ||||
| 12,3 | 2,2 | 0,6 | 1,32 | 4,84 | 0,36 | ||
| 12,6 | 2,5 | 1,6 | 6,25 | 2,56 | |||
| 12,7 | 2,6 | 2,6 | 6,76 | 6,76 | 6,76 | ||
| 12,9 | 2,8 | -0,4 | -1,12 | 7,84 | 0,16 | ||
| 2,9 | 3,6 | 10,44 | 8,41 | 12,96 | |||
| 13,2 | 3,1 | 2,6 | 8,06 | 9,61 | 6,76 | ||
| 13,3 | 3,2 | 3,6 | 11,52 | 10,24 | 12,96 | ||
| Итого | 253,7 | 119,32 | 138,66 | 142,2 |
Таким образом,

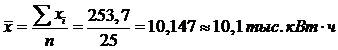
 ,
,

Определим линейный коэффициент корреляции:

1.
5. Подбор уравнения регрессии представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные сх, не учитывать. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у со значениями факторного признака х.
Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими. Они обычно обозначаются  (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.
(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.  = f(x). (Иногда для простоты записи вместо
= f(x). (Иногда для простоты записи вместо  пишут
пишут  .)
.)
Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей.
Для аналитической связи между х и у могут использоваться следующие простые виды уравнений:
 – прямая линия;
– прямая линия;  – парабола;
– парабола;
 – гипербола;
– гипербола; 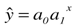 – показательная функция;
– показательная функция;
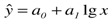 – логарифмическая функция и др.
– логарифмическая функция и др.
Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные — криволинейными зависимостями.
Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака  должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.
должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.
 .
.
Поставив данное условие, легко определить, при каких значениях  ,
,  и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной.
и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной.
 (2)
(2)
Перейдём к построению уравнения регрессии. Так как корреляционное облако показывает наличие линейной связи, поэтому будем использовать функцию:
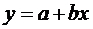
Определим параметры уравнения a и b.
 ,
,
 .
.
Полученное уравнение связи (уравнение регрессии) выражает функциональную зависимость y от x.
Параметр a характеризует значение результативного признака y при значении факторного признака x = 0. В нашем примере a = -2,29, что означает условную производительность труда при нулевой энерговооружённости, то есть мы не можем даже смоделировать современное производство, которое существовало бы без использования электроэнергии.
Параметр b, который называется коэффициентом регрессии, характеризует, в какой мере результативный признак y увеличивается с ростом величины факторного признака x.
В нашем примере прирост энерговооружённости труда на 1 тыс. кВт∙ч в год на одного сотрудника даёт прирост производительности труда на 860 шт. изделий в год на одного сотрудника.
;
Для иллюстрации построим график эмпирической (маркеры-кружочки) и теоретической (маркеры-квадратики) линий регрессии.

Рис.6. График эмпирической и теоретической линий регрессии.
^
6. Теоретическое корреляционное отношение представляет собой универсальный показатель тесноты связи. Измерить тесноту связи между коррелируемыми величинами – это значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака. Ранее были рассмотрены показатели, с помощью которых можно выявить наличие корреляционной связи между двумя признаками x и y и измерить тесноту этой связи: коэффициент Фехнера и линейный коэффициент корреляции.
Наряду с ними существует универсальный показатель – корреляционное отношение (или коэффициент корреляции по Пирсону), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционные отношения. Эмпирическое корреляционное отношение рассчитывается на основе правила сложения дисперсий как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии, т.е.
 . (2)
. (2)
Теоретическое корреляционное отношение  определяется на основе выравненных (теоретических) значений результативного признака
определяется на основе выравненных (теоретических) значений результативного признака  , рассчитанных по уравнению регрессии.
, рассчитанных по уравнению регрессии.  представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отклонением в ряду эмпирических значений. Если обозначить дисперсию эмпирического ряда игреков через
представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отклонением в ряду эмпирических значений. Если обозначить дисперсию эмпирического ряда игреков через  , а теоретического ряда –
, а теоретического ряда –  , то каждая из них выразится формулами:
, то каждая из них выразится формулами:
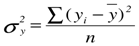 , (2)
, (2)
 . (2)
. (2)
Сравнивая вторую дисперсию с первой, получим теоретический коэффициент детерминации:
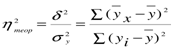 , (2)
, (2)
который показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение:
 . (2)
. (2)
Оно может находиться в пределах от 0 до 1. Чем ближе его значение к 1, тем теснее связь между вариацией y и x. При 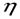 <0,3 говорят о малой зависимости между коррелируемыми величинами, при 0,3<
<0,3 говорят о малой зависимости между коррелируемыми величинами, при 0,3< 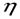 <0,6 – о средней, при 0,6<
<0,6 – о средней, при 0,6< 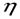 <0,8 – о зависимости выше средней, при
<0,8 – о зависимости выше средней, при 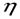 >0,8 – о большой, сильной зависимости. Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. При линейной зависимости
>0,8 – о большой, сильной зависимости. Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. При линейной зависимости  .
.
В нашей задаче расчет необходимых сумм для использования в формуле (2) приведен в последних двух столбцах таблицы 12. Тогда теоретический коэффициент детерминации по формуле (2) равен: 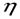 2 теор = 38762,125 / 42818 = 0,9053, то есть дисперсия, выражающая влияние вариации фактора x на вариацию y, составляет 90,53%.
2 теор = 38762,125 / 42818 = 0,9053, то есть дисперсия, выражающая влияние вариации фактора x на вариацию y, составляет 90,53%.
Теоретическое корреляционное отношение по формуле (2) равно: 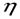 теор =
теор =  = 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами.
= 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами.
^
Контрольные задания по теме
На основе исходных данных контрольных заданий по теме 2 определить наличие и характер корреляционной связи между признаками x и y 6-ю методами.
| При-знак | Вариант | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| x | Рост | Доход | Возраст | IQ | Доход | Возраст | рост/вес | Стаж | Доход | IQ |
| y | Вес | Вес | Доход | Доход | Тетрадь | рост/вес | Кол-во друзей | Доход | Кол-во друзей | Время решения |
Тема 6. Корреляционно-регрессионный анализ
Цель: изучение видов взаимосвязей явлений (функциональная, корреляционная); видов корреляционной зависимости; способов определения тесноты связи; усвоение смысла показателей регрессии.
После изучения вы сможете: определять силу тесноты связи между социально – экономическими показателями, давать интерпретацию параметров управления регрессии.
Информационные источники:
1. Курс теории статистики: Учебник/Под ред. В.Н. Салина, Э.Ю. Чурикова. – М.: Финансы и Статистика, 2006.
2. Годин А.М. Статистика: Учебник. – М.: Дашков и К’, 2008.
3. Статистика: Учебник/Под ред. И.И. Елисеевой. – М.: Крокус, 2008
4. Теория статистики: Учебник/Под ред. Г.П. Громыко. – М.: ИНФРА-М, 2000.
5. Галкина В.А. Статистика: Учебное пособие: М.: РГАЗУ,2002.
Содержание темы: исследование объективно существующих связей; количественные оценки тесноты связи; регрессионный анализ; показатели тесноты связи (параметрические, ранговые).