Действующие программы по математике требуют развития у детей самостоятельности в решении текстовых задач. Каждый выпускник начальной школы должен уметь кратко записывать условия задачи, иллюстрируя ее с помощью рисунка, схемы или чертежа, обосновывать каждый шаг в анализе задачи и ее решении, проверять правильность решения. Умение решать текстовые задачи является одним из основных показателей уровня математического развития ребёнка, глубины усвоения им учебного материала.
Не все учащиеся умеют и любят решать задачи. Это происходит потому, что дети не научены анализировать данные, видеть взаимосвязь между искомым и данным, структурировать ход решения. А при отсутствии потребности в глубоком осмыслении описанных в задаче связей у ребёнка формируется прочная привычка сводить решение к простому вычислению.
Младший школьный возраст является началом формирования учебных действий у детей. В то же время моделирование – это действие, которое выносится за пределы младшего школьного возраста в дальнейшие виды деятельности человека и выходит на новый уровень своего развития. С помощью моделирования можно свести изучение от простого, незнакомого - к знакомому, то есть сделать объект доступным для тщательного изучения.
Для чего же младшим школьникам необходимо овладеть методом моделирования?
Во – первых, введение в содержание обучения понятий модели и моделирования существенно меняет отношение учащихся к учебному предмету, делает их учебную деятельность более осмысленной и более продуктивной.
Во- вторых, целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.
Для того чтобы вооружить учащихся моделированием как способом познания, нужно, что бы школьники сами строили модели, сами изучали какие- либо объекты, явления с помощью моделирования.
Одним из наиболее эффективных для формирования действия моделирования типов заданий являются текстовые задачи. Чтобы решить задачу, надо построить её математическую модель.
Работа над текстовой задачей начинается с того что её читает ученик. Для того чтобы решить задачу, учащийся должен уметь переходить от текста (словесной модели) к представлению ситуации (мысленной модели), а от неё - к записи решения с помощью математических символов (знаково-символической модели).
Все эти модели являются описанием одного и того же объекта - задачи. Они отличаются друг от друга тем,что выполнены на разных языках: языке слов (словесная); языке образов (мысленная); языке математических символов (знаково-символическая).
Слово «модель» в переводе с французского означает «образец».
Модель – это в некотором смысле копия, она может быть упрощена и позволяет лучше, полнее изучать оригинал.
Модель строят на 1-м этапе решения задачи для того, чтобы понять задачу.
По видам средств, используемых для построения, все модели можно разделить на схематизированные и знаковые.
Схематизированные модели делятся на:
1.Вещественные (предметные):
- из оригиналов (тетради, карандаши, конфеты…);
- из копий, внешне похожих на оригиналы (утята, котята, огурцы…);
- из фишек без сохранения сходства с оригиналами.
При вещественном моделировании выполняются конкретные действия руками.
2.Графические, в зависимости от того, какое действие они обеспечивают.
-рисунок(сюжетный, предметный)
-условный рисунок
-схема
- чертеж
К знаковым моделям, выполненным на естественном языке можно отнести краткую запись текстовой задачи, таблицы. Знаковыми моделями текстовых задач, выполненными на математическом языке, являются: формула, выражение, уравнение, система уравнений, запись решения задачи по действиям.
Визуализация текстовой задачи – это использование моделей (средств наглядности) для нахождения значений величин, входящих в задачу, данных и искомых чисел, а также для установления связи между ними.
Методика обучения моделированию текстовых задач включает следующие этапы:
I этап: подготовительная работа к моделированию текстовых задач;
II этап: обучение моделированию текстовых задач;
III этап: закрепление умения решать задачи с помощью моделирования.
Подготовительная работа начинается ещё до школы и продолжается в первом классе. Для этого в работе используем вещественные (предметные) модели:
- из оригиналов (игрушки, тетради, карандаши, конфеты, фрукты, овощи…);
- из копий, внешне похожих на оригиналы (утята, котята, огурцы…);
- из фишек без сохранения сходства с оригиналами.
При вещественном моделировании выполняются конкретные действия руками, инсценировка.
На подготовительном этапе учащиеся учатся иллюстрировать данные задачи с помощью картинок, при этом осуществляют операции объединения множеств и удаления подмножества из данного множества.
Отображая эти действия графически, сначала в виде рисунка, затем в виде модели, учащиеся в дальнейшем подходят к знаково-символической форме: равенству, формуле, уравнению и так далее.
Рисунок изображает реальные предметы, о которых говорится в задаче, или условные предметы в виде геометрических фигур. Знакомство с этой моделью начинаю с начала 1 класса. Во-первых, рисование- любимый вид деятельности малышей, во-вторых, приём хорош для развития моторики рук, в-третьих, рисование является развивающим упражнением.
Рисунок бывает:сюжетный, предметный, условный.
В целях формирования осознанного подхода к составлению и применению моделей в виде рисунка в учебнике к задаче даю следующие задания:
-какой рисунок подходит к данной задаче?
-составь по другому рисунку задачу и реши её.
Эти задания способствуют формированию навыка составления и анализа моделей.
Чертёж. Применяю тогда, когда числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины.
Схема. Можно применять эту модель на материале обратных задач, при решении задач разными способами.
Схема является наиболее предпочтительной моделью при решении задач по ряду причин:
- может быть использована при решении задач со сколь угодно большими числами;
- может применяться при решении задач с буквами;
- позволяет подняться на достаточно высокую ступень абстрактности;
- помогает научить детей решать задачи – а значит научить их устанавливать связи между данными и искомым и в соответствии с этим выбирать, а затем и выполнять арифметические действия.
Блок-схема (разбор задачи аналитическим способом, то есть с вопроса). Изучение этой модели возможно уже в конце 2-го класса, когда все предыдущие модели изучены хорошо, широко и системно используются на уроке.
Краткая запись. С этой моделью начинаю работать в 1-м классе. Удачно вводить краткую запись параллельно с рисунком. Позднее переходим на стандартную краткую запись в зависимости от типа задач.
Таблица.
Таблица- это вид модели, похожий на краткую запись. Она предполагает уже хорошее знание зависимости пропорциональных величин, так как сама таблица этой взаимозависимости не показывает. Данная табличная модель служит формой фиксации анализа сюжетной задачи и является основным средством поиска решения. Пользуясь такой схемой, нетрудно найти план и осуществить решение задачи.
Для формирования умения составлять схемы к условиям задач использую следующие виды заданий:
-нужно перевести текст задачи в чертеж;
-нужно по схеме составить задачу;
-нужно из предложенных вариантов выбрать и соотнести текст задачи и подходящий к нему чертеж.
Таким образом, процесс моделирования задачи повышает мыслительную активность детей, способствует развитию логического, абстрактного мышления, а, значит, делает процесс решения задач более приятным и интересным. Использование графического моделирования при решении текстовых задач обеспечит более качественный анализ задачи, осознанный поиск ее решения, обоснованный выбор арифметических действий и предупредит многие ошибки в решении задач. Также весьма важным является создание моделей на глазах у детей или самими учащимися в процессе решения задачи, поскольку это обеспечивает глубокое понимание задачи, усвоение связей между данными и искомым.



Решите кейсы
1. Почему в основе формирования умения решать задачи, по мнению многих методистов (А.В. Белошистая, Т.Е. Демидова, А.П. Тонких, Л.М. Фридман и др.), лежит такой прием, как моделирование? Дайте характеристику этого приема. Приведите примеры использования различных моделей при решении задач, используя работы перечисленных выше авторов.
Моделирование — это замена действий с обычными предметами действиями с их уменьшенными образцами, моделями, муляжами, макетами, а также их графическими заменителями: рисунка, чертежа, схемами. Словесная форма представления информации в процессе обучения не универсальна и не оптимальна, что объясняет стремление учителей более широко использовать на уроках разнообразные графические средства. Моделирование помогает ребенку лучше сориентироваться в задаче.
Моделирование –целенаправленный информационный процесс, обеспечивающий получение новой информации об объекте, его свойствах и поведении с помощью модели. Модель – упрощенное материальное или информационное представление (образ) реального объекта, частично воспроизводящее объект, его свойства и поведение. Результат моделирования – новая информация о существующем объекте, его свойствах и поведении, либо прогноз свойств и поведения конкретной новой, ранее не существовавшей, модификации объекта.
Белошистая А.В.
Решение текстовых задач геометрическим методом в курсе математики начальной школы Т.Е. Демидова, А.П. Тонких


2. Сделайте краткую запись задачи: «В зале в первом ряду сидели 7 человек, а во втором на 3 человека больше. Сколько человек было в первом и во втором ряду вместе?» Подумайте, какую работу нужно организовать учителя при решении задачи, какие приемы обучения использовать. С какими задачами можно сравнить данную? Сделайте для этих задач краткую запись. Конкретизируйте на примере данной задачи прием преобразования (вопроса, условия, одного из данных).

Учебник 1 класс.
Авторы:
М.И. Моро, С.И. Волкова, С.В. Степанова

Решение задач с ребенком:


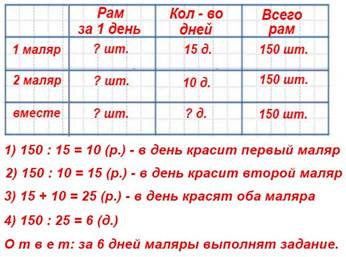
3. Какую ошибку могут допустить обучающиеся при решении задачи: «Нужно покрасить 150 рам. Один маляр может это сделать за 15 дней, другой за 10. За сколько дней выполнят эту работу оба маляра, если будут работать вместе?» Как предупредить появление ошибки? Составьте беседу для разбора задачи.
Дети могут просто сложить количество дней работы двоих моляров. Не подумав, что нужно разделить это число на количество рам, которые нужно покрасить.
Сколько дней нужно одному маляру, чтобы покрасить 150 рам?
Сколько рам покрасит один моляр за 15 дней?
Сколько дней нужно другому маляру, чтобы покрасить 150 рам?
Сколько рам покрасит другой моляр за 15 дней?
Сколько рам нужно будет покрасить обоим малярам?
Сначала надо узнать сколько покрасит один маляр за 1 день и другой маляр за 1 день. Потом мы узнаем сколько они покрасят вместе за 1 день.
Затем, известное количество рам мы должны разделить на количество рам, которые красят два маляра вместе за 1 день.