Алгоритм оптимизации по модульному оптимуму
Под оптимизацией СПР понимают приведение передаточных функций замкнутых контуров в соответствии с некоторыми требованиями, которые накладываются на частотные характеристики контуров, выполнение которых обеспечивает удовлетворительное протекание переходных процессов.
Параметры оптимизированных контуров могут быть получены в результате решения некоторого функционала, удовлетворяющего реализации заданного условия. При этом решение может быть довольно сложным. Поэтому на практике применяют достаточно простой способ, основанный на исследовании формы АЧХ замкнутой системы.
При АЧХ замкнутой системы в виде кривой 1 (рис.10.3) в системе будет иметь место колебательный переходный процесс, причем колебательность процесса определяется величиной резонансного максимума Мр: чем выше Мр, тем больше будет перерегулирование s переходной функции h(t).
Для достижения приемлемого (малого) перерегулирования s нужно, чтобы Мр был минимальным. Этому требованию удовлетворяет АЧХ вида 2, что соответствует характеристике пропорционального звена. Однако, как отмечалось выше, система в этом случае нереализуема.
Поэтому в качестве желаемой АЧХ предпочитают использовать характеристику вида 3. Для ее реализации необходимо выполнение следующих условий:
; 
; …; 
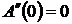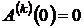, (1)
где параметр k, определяющий количество уравнений, равен количеству варьируемых параметров.
При решении системы уравнений (1) приходится иметь дело с радикалами. Поэтому во избежание этого рассматривают производные квадрата АЧХ:
; 
; …; 
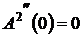. (2)
Выбор параметров САР в соответствии с условиями (2) предложено называть оптимизацией по модульному оптимуму [3].
Вначале ПФ замкнутой системы записывают в нормированном виде:
. (3)
Затем определяют квадрат АЧХ:
, (4)
где 
; (5)
; 
; 
; …; 
;
; 
; 
; …; 
;
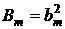Можно показать [3], что из (2) с учетом (4) можно получить следующие условия оптимизации:
; 
; …; 
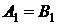. (6)
В частном случае, когда числитель (5) равен единице (
), условие оптимизации принимает вид:
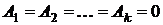. (7)
Оптимизация одноконтурных СПР
Рассмотрим одноконтурные однократноинтегрирующие (т.е., с астатизмом 1-го порядка по управлению), которые без ошибки в установившемся режиме воспроизводят постоянное воздействие.
Методику оптимизации рассмотрим на примерах.
Задача 1. Объект содержит одну малую постоянную времени.
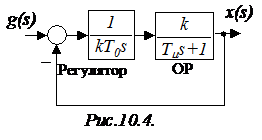В этом случае астатическая система 1-го порядка состоит из последовательно соединенных интегрального регулятора и объекта регулирования, инерционность которого характеризуется малой постоянной времени Tm (рис.10.4).
Определить параметр регулятора T0 из условия модульного оптимума, а также динамические свойства оптимизированной системы.
Решение. Передаточная функция замкнутой системы:
. (8)
Сравнивая передаточную функцию (8) с (3), определяем, что
; 
; 
; 
.
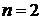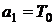Поскольку определению подлежит значение только одного параметра, то по (7) составляем одно условие оптимизации:
,
решая которое относительно Tm, получаем значение параметра:
. (9)
Для определения динамических свойств оптимизированной системы передаточную функцию (8) колебательного звена представим в стандартной форме:
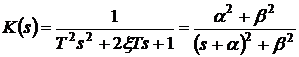, (10)
где 
; 
; 
;
; 
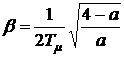. (11)
Передаточной функции (10) соответствует переходная фун-я (рис.10.5):
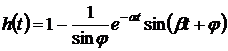, (12)
где 
.
Из (12) можно получить выражения для основных прямых показателей качества переходного процесса [3]:
;
;
. (13)
Графики зависимостей 
и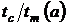 
представлены на рис.10.6.
В соответствии с (9) параметр a =2. При этом показатели (11) оказываются равными:
; 
;
; 
,
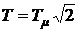а показатели качества (13) –
; 
; 
.
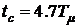Таким образом, оптимизация системы (рис.10.4) по модульному оптимуму в соответствии с (9) привела к тому, что передаточная функция замкнутой системы соответствует колебательному звену с коэффициентом демпфирования . Реакция такой системы на скачкообразное воздействие имеет перерегулирование и время первого согласования с установившимся значением .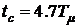
ЛАЧХ оптимизированного разомкнутого контура имеет вид "–1–2" (рис.10.7). При этом частота среза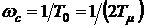 
вдвое меньше частоты сопряжения 
.
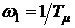Для приводов отдельных механизмов часто принимают a >2, то есть, уходят от настройки системы по модульному оптимуму. Например, при а= 4 мы имеем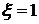 
, а перерегулирование вообще отсутствует (см. рис.10.6). Обычно это электроприводы экскаваторов, в которых колебательность переходных процессов стремятся исключить. Однако следует помнить, что повышение а связано с тем, что Т0 растет. Это приводит к тому, что снижается частота среза wс ЛАЧХ разомкнутого контура, а это говорит об уменьшении быстродействия системы.
Задача 2. Объект содержит одну большую и одну малую инерционность.
В этом случае система состоит из последовательно соединенных пропорционально-интегрального регулятора (используется вместо интегрального регулятора для повышения быстродействия системы) и объекта регулирования (рис.10.8), причем Tb – большая, Tm – малая постоянные времени.
Определить параметры регулятора T0, T1 из условия модульного оптимума.
Решение. Передаточная функция замкнутой системы:
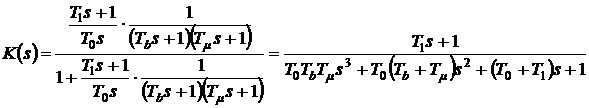. (14)
Сравнение с (9) дает:
; 
; 
; 
; 
; 
.
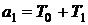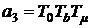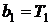Условия оптимизации имеют вид:
решение которых относительно искомых постоянных времени дает:
; 
,
где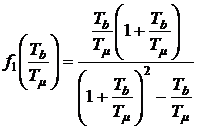 
; 
.
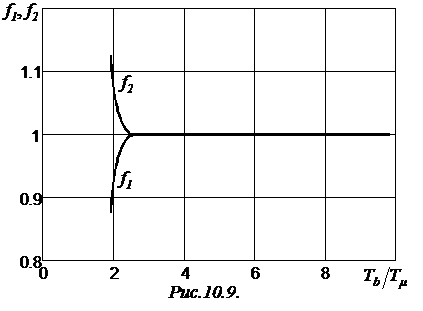Анализируя соответствующие графические зависимости (рис.10.9), приходим к выводу, что если большая постоянная времени в 2 и более раз превышает малую, то 
, и с достаточной степенью точности получим условия оптимизации:
; 
. (15)
Таким образом, если в объекте регулирования присутствуют одна большая Tb и одна малая Tm постоянные времени, то действие большой постоянной времени следует скомпенсировать действием регулятора (введением форсировки).
Это свойство оптимизации можно распространить и на тот случай, когда в объекте присутствуют N больших постоянных времени – тогда все они должны быть скомпенсированы регулятором. Так, если ПФ объекта имеет вид:
,
то при оптимизации одноконтурной системы передаточную функцию регулятора следует выбрать в виде:
.
Задача 3. Объект содержит, помимо больших, несколько малых постоянных времени, распределенных как по прямому каналу регулирования, так и по каналу обратной связи.
Это более общий, наиболее близкий к практике случай. После компенсации коэффициента усиления и больших постоянных времени объекта структурная схема системы приводится к виду, представленному на рис.10.10.
Определить параметры регулятора T0, T1 из условия модульного оптимума.
Решение. Передаточная функция замкнутой системы:
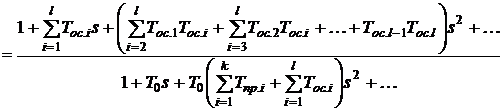. (16)
Условие оптимизации:
.
Решая это уравнение с учетом (16) относительно T0, получаем оптимальное значение постоянной времени:
, (17)
где 
– сумма всех малых инерционностей (прямого канала и канала ОС):
.
Для оценки качества переходного процесса в оптимизированной системе со многими малыми постоянными времени она может быть аппроксимирована [3] простейшей структурной схемой (рис.10.11) с одной эквивалентной постоянной времени
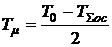, (18)
отражающей инерционность ОР, и эквивалентной постоянной интегрирования разомкнутого контура
. (19)
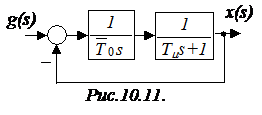Это эквивалентно аппроксимации передаточной функции (16) передаточной функцией
. (20)
Передаточная функция (20), так же, как и передаточная функция (8) соответствует колебательному звену с коэффициентом демпфирования со всеми вытекающими отсюда свойствами.
Такая аппроксимация не искажает информации о первых трех коэффициентах ошибок контура
; 
; 
,
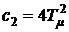и поэтому вполне допустима.
Рассмотрим частный случай, когда инерционности в канале ОС отсутствуют (
). Из уравнений (17) – (19) следует, что в этом случае:
; 
.
Таким образом, при отсутствии инерционностей в цепи ОС эквивалентное значение Tm равно сумме всех инерционностей прямой части системы.
Для другого частного случая предположим, что на входе системы установлен фильтр (апериодическое звено), передаточная функция которого (в общем случае с точностью до постоянного множителя) равна передаточной функции цепи ОС, то передаточная функция системы будет определяться выражением (16), в котором полином числителя будет равен единице. В результате можно получить условие оптимизации:
; 
.
То есть, инерционность такой системы равна сумме инерционностей прямой цепи и цепи ОС. Установка фильтра на входе системы эквивалентна переносу инерционностей из канала ОС в прямой канал.
Оптимизация многоконтурных СПР
Одноконтурные СПР имеют наиболее высокие динамические показатели. Однако при большом количестве больших инерционностей объекта возникают затруднения, связанные с необходимостью реализации сложных передаточных функций регуляторов. Поэтому на практике распространение получили многоконтурные СПР, объект регулирования для каждого контура которых содержит одну (максимум две) большие постоянные времени.
Особенность построения многоконтурных СПР состоит в том, что каждый последующий k -й контур регулирования состоит из замкнутого (k–1)-го контура регулирования, объекта и регулятора. Оптимизацию выполняют, начиная с самого внутреннего контура, который при оптимизации следующего контура представляют аппроксимированной передаточной функцией (20). Большие постоянные времени объекта компенсируются регулятором, поэтому обобщенная структура, например, 2-контурной СПР может быть представлена в виде, показанном на рис.10.12, где обозначено: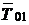 
– эквивалентная постоянная интегрирования аппроксимированного первого контура регулирования; 
– эквивалентная малая постоянная времени первого контура регулирования; 
– постоянная интегрирования разомкнутого второго контура регулирования.
В соответствии с алгоритмом, изложенным выше, можно получить оптимальное значение постоянной интегрирования разомкнутого контура двухконтурной системы:
, (21)
где 
– сумма малых постоянных времени, расположенных в прямом канале 2-го контура;
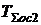– сумма малых постоянных времени, расположенных в канале ОС 2-го контура.
В частном случае, когда ОС 2-го контура безынерционная, вместо (21) может быть использована формула:
.
Этот же результат можно получить если внутренний контур заменим апериодическим звеном с постоянной времени 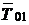, то есть, 
.
Оптимизация третьего и последующих контуров осуществляется аналогичным образом. При этом второй замкнутый контур регулирования представляется колебательным звеном с передаточной функцией:
,
где 
, 
.