Введение
1. Расчёт срока службы привода
2. Выбор двигателя. Кинематический расчет двигателя
3. Выбор материала зубчатой передачи. Определение допускаемых напряжений
4. Расчет зубчатой передачи
5. Расчёт нагрузок валов редуктора
6. Проектный расчёт валов
7. Эскизная компоновка редуктора
8. Проверочный расчет тихоходного вала
9 Конструирование зубчатого колеса
10. Подбор шпонок и проверочный расчет шпонок
Литература
Введение
В производственных машинах необходим большой вращающий момент при угловой скорости, меньшей, чем у двигателя. Для передачи движения от двигателя к производственной машине и изменения при этом угловой скорости и вращающего момента служат различные передаточные механизмы. Зубчатый, или червячный, передаточный механизм, предназначенный для уменьшения угловых скоростей и представляющий систему зубчатых колес в отдельном закрытом корпусе, непроницаемом для масла и пыли и одновременно являющемся масляной ванной для механизма, называется редуктором. Размещение опор валов редуктора в одном общем жестком корпусе обеспечивает постоянство относительного расположения осей валов, а это позволяет применять широкие колеса с малым модулем. Применение малых модулей, в свою очередь, приводит к увеличению точности и уменьшению уровня шума при работе передачи, к снижению стоимости ее изготовления. Обильное смазывание способствует малому износу и повышает КПД редукторной передачи. Наличие корпуса обеспечивает безопасность работы редукторов. Этими достоинствами редукторов объясняется вытеснение ими открытых передач.
По виду звеньев передачи редукторы делятся на цилиндрические (оси ведущего и ведомого валов параллельны), конические (оси валов пересекаются), червячные (оси валов перекрещиваются в пространстве). Встречаются и комбинированные редукторы, представляющие сочетания зубчатых (цилиндрических и конических) и червячных передач.
Одноступенчатый цилиндрический редуктор обычно применяют при передаточном числе U<7. Одноступенчатый редуктор наиболее прост и надежен в работе. Применяется для мощностей до 40000кВт.
Двухступенчатые цилиндрические редукторы обычно применяются при передаточном числах U<40. Первая (быстроходная) ступень редуктора во многих случаях имеет косозубые колеса: тихоходная ступень может быть выполнена с прямозубыми колесами. Не менее часто применяются редукторы, у которых обе ступени имеют колеса одинакового вида (прямозубые, косозубые и шевронные).
Трехступенчатый цилиндрический редуктор обеспечивает передаточное число U<150 и выше. Достоинство данной схемы - симметричное расположение зубчатых колес всех ступеней.
Коническо-цилиндрический двухступенчатый редуктор применяют при пересекающихся осях ведущего и ведомого валов. Передаточное число такого редуктора обычно не выше 25.
При необходимости получения различных угловых скоростей выходного вала в корпусе редуктора размещают несколько пар зубчатых колес с различными передаточными числами и специальный механизм переключения, который может включать по мере надобности ту или иную пару зубчатых колес. Такие передаточные механизмы называют коробками передач.
1. Расчёт срока службы привода
1.1 Принимаем в соответствии с заданием: работу привода в 2 смены, нагрузку малоизменяющуюся, режим реверсивный, продолжительность смены 8 часов
1.2 Определяем ресурс работы привода:
Lh = 365*Lr* tc*Lc = 365*5*8*2 = 29200(чac)
где:
Lr - срок службы привода, лет
tc - продолжительность смены, час
Lc – число смен
1.3 Принимаем время простоя машинного агрегата 15% ресурса, тогда Ln будет представлять собой следующую формулу:
Ln = 0,85 *Lh = 0,85*29200= 24820(чac)
1.4 Составляем табличный ответ решения:
| Lr, лет | tc,мчас | Lc | Ln, Час | Характер нагрузки | Режим работы |
| Малоизме-няющаяся | Реверсивный |
Выбор двигателя. Кинематический расчет двигателя
2.1 Определение мощности и частоты вращения двигателя
2.1.1 Определяем требуемую мощность рабочей машины
Pрм = F*V = 1,2*0,8 = 0,96(кВт)
где
F - значение тяговой силы, кH
V - линейная скорость тяговой цепи, м/сек
2.1.2 Определяем общий коэффициент полезного действия привода:
h = h*h*h*h*h2пк = 0,965*0,965**0,98*0,985*0,9922=0,885
где
hп - КПД редуктора, принимаем 0,965
hоп - КПД открытой передачи, принимаем 0,965
hм - КПД муфты, принимаем 0,98
hпк - КПД подшипников качения, принимаем 0,992
hпс - КПД подшипников скольжения, принимаем 0,985
2.1.3 Определяем требуемую мощность двигателя:
Pном = Pрм / h = 0,96 / 0,885 = 1,09(кВт)
где:
Ррм - мощность рабочей машины, Квт
h - общий КПД
Принимаем двигатель серии 4АМ80B6УЗ с номинальной мощностью Рном = 1,1 (кВт), и частотой вращения при номинальном режиме nном = 920 (об/мин).
2.1.4 Определяем частоту вращения приводного вала рабочей машины:
nрм = 60*1000*V = 60*1000*1,7 = 76,4(об/мин)
р*Д 3,14*200
где
Д- диаметр барабана,мм
V- скорость тягового органа,м/сек.
2.1.5 Определяем передаточное отношение привода для принятого типа двигателя при заданной мощности:
Uном = nном / nрм = 920/ 76,4 = 12, 04(об/мин)
где
nном - номинальная частота вращения двигателя, об/мин;
nрм - частота вращения приводного вала рабочей машины, об/мин.
2.1.6 Принимаем передаточное отношение закрытой передачи по СТ СЭВ 221-75 равным: Uзп = 5,0
2.1.7 Определяем передаточное отношение открытой передачи:
Uоп = Uном / Uзп = 12,04 / 5,0 = 2,41
2.2 Определение силовых и кинематических параметров привода
2.2.1 Определяем мощность валов привода
а) Вал двигателя:
Pдв = Pном =1,1(кВт)
б) Быстроходный вал:
P1 = Pдв*hм*hпк = 1,1*0,98*0,992= 1,07(кВт)
где
hоп - КПД открытой передачи
hм - КПД муфты
в) Тихоходный вал:
Р2 = Р1*h*h = 1,1*0,965*0,992 = 1,02(кВт)
где
hзп - КПД редуктора
h - КПД подшипников качения
г) Вал рабочей машины:
= 2*h*h = 1,1*0,965*0,985 = 0,97(кВт)
где
hоп - КПД открытой передачи
hпс - КПД подшипников скольжения
2.2.2 Определяем угловую скорость валов привода
а) Вал двигателя:
wном = p*nном / 30 = 3,14*920 / 30 = 96,29(рад/с)
где
nном-номинальная частота вращения двигателя
б) Быстроходный вал:
w1 = wном/ Uоп =39,95(рад/с)
Uоп - передаточное число открытой передачи
в) Тихоходный вал:
w2 = w1 / Uзп = 39,95/ 5,0 = 7,99(рад/с)
где
w1 - угловая скорость быстроходного вала
Uзп - передаточное число закрытой передачи в соответствии СТ СЭВ 221-75, принимаем 5,0
г) Вал рабочей машины:
щрм = щ2 = 7,99(рад/с)
где
w2 - угловая скорость тихоходного вала.
2.2.3 Определяем вращающий момент валов привода:
а) Вал двигателя:
Тдв = Рдв / wном = 1100/ 96,29 = 11,42(Н*м)
где
Pдв - мощность на валу двигателя
wном - номинальная угловая скорость
б) Быстроходный вал:
T1 = Тдв*U*h*hпк= 11,42*2,41*0,965*0,992 = 26,35(Н*м)
где
Тдв - вращающий момент двигателя
пк - КПД подшипников качения
hоп - КПД открытой передачи
г) Тихоходный вал:
Т2=Т1*Uзп*hзп*hпк= 26,35*5,0*0,965*0,992 = 126,10(Н*м)
где
Т1 - вращающий момент быстроходного вала
Uзп - передаточное число закрытой передачи
h - КПД закрытой передачи
hк - КПД подшипников качения
в) Вал рабочей машины:
Трм = Т2* hм*hпс = 126,10*0,98*0,985 = 121,73(Н*м)
где
Т2 - вращающий момент тихоходного вала
hс - КПД подшипников скольжения
hм - КПД муфты
2.2.4 Определяем частоту вращения валов привода:
а) Вал двигателя:
nтабл= nном = 920(об/мин)
где
nном - номинальная частота вращения двигателя
б) Быстроходный вал:
n1 = nном /Uоп = 381,74(об/мин)
где
n1 - частота вращения быстроходного вала
nном - номинальная частота вращения двигателя
Uоп - передаточное число открытой передачи
в) Тихоходный вал:
n2 = n1 / Uзп = 381,74/ 5,0 = 76,35(об/мин)
где
n1 - частоту вращения быстроходного вала
Uзп - передаточное число закрытой передачи
г) Вал рабочей машины
nрм = n2 = 76,35(об/мин)
где
n2 - частота вращения тихоходного вала.
2.2.5 Составляем табличный ответ решения задачи:
Таблица. Силовые и кинематические параметры привода
| Тип двигателя 4АМ80В6УЗ; Р=1,1(кВт); n=920(об/мин) | |||||||
| Параметр | Передача | Параметр | Вал | ||||
| Закрытая (редуктор) | открытая | двигателя | Редуктора | Приводной рабочей машины | |||
| быстроходный | тихоходный | ||||||
| Переда-точное число U | 5,0 | 2,41 | Расчетная мощность Р, кВт | 1,1 | 1,07 | 1,02 | 0,97 |
| Угловая скорость w, 1/с | 96,2 | 39,95 | 7,99 | 7,99 | |||
| КПД h | 0,965 | 0,965 | Частота вращения n, об/мин | 381,74 | 76,35 | 76,35 | |
| Вращающий момент Т, Н*м | 11,42 | 26,35 | 126,10 | 121,73 |
3. Выбор материала зубчатой передачи. Определение допускаемых напряжений
3.1 Назначаем твердость, термообработку и материал
а)для шестерни: 40Х, твердость 269…302 НВ, термообработка - улучшение.
б)колесо марка стали 40Х, твердость 235…262 НВ, термообработка
3.2 Определяем среднюю твердость шестерни и колеса:
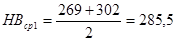 (HB)
(HB)
 (HB)
(HB)
3.3 Определяем число циклов переменных напряжений за весь срок службы для шестерни и колеса:
N1 = 573 *w1* Ln= 573*39,95*24820=5,6816*108
N1 = 573*w2* Ln= 573*7,99*24820=1,1363*108
где
w1 и w2 - угловые скорости быстроходного и тихоходного валов, с-1
Ln - рабочий ресурс двигателя, час
3.2.2 Принимаем число циклов переменных напряжений для шестерни и колеса:
Nно1 = 22,8*106 (млн. циклов)
Nно2 = 16,29*106 (млн. циклов)
где
Nно- число циклов перемены напряжений соответсвующих выносливости циклов
3.2.3 Определяем коэффициент долговечности для шестерни и колеса:
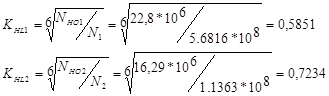
где
Nно - число циклов переменных напряжений соответствующих пределу выносливости
N - число циклов переменных напряжений за весь срок службы привода.
Принимаем KHL1= KHL2 =1, т.к. N > Nно
3.2.4 Определяем допускаемое контактное напряжение для шестерни и колеса, соответствующих числу циклов переменных напряжений:
 (Н/мм2)
(Н/мм2)
 (Н/мм2)
(Н/мм2)
3.2.5 Определяем допускаемое контактное напряжение для зубьев шестерни и колеса:
 (Н/мм2)
(Н/мм2)
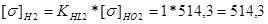 (Н/мм2)
(Н/мм2)
Принимаем [s]H = 514,3 Н/мм2, т.к. рассчитываем по менее прочным зубьям.
3.2.6 Определяем коэффициент долговечности зубьев шестерни и колеса для определения допускаемых напряжений изгиба:
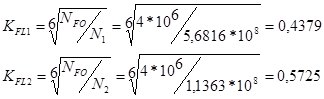
Где NFO1, NFO2 - число циклов переменных напряжений для зубьев шестерни и колеса соответствующему пределу выносливости, для всех сталей принимаем равным 4*106 циклов
N1, N2 - число циклов переменных напряжений за весь срок службы привода
3.2.7 Определяем напряжение изгиба соответствующему пределу изгибной выносливости для зубьев шестерни и колеса:
 (Н/мм2)
(Н/мм2)
 (Н/мм2)
(Н/мм2)
3.2.8 Определяем допускаемое напряжение изгиба зубьев шестерни и колеса:
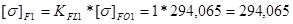 (Н/мм2)
(Н/мм2)
 (Н/мм2)
(Н/мм2)
3.1.9 Примем значения[у]F1 и [у]F2 на 25% меньше расчётного:
 (Н/мм2)
(Н/мм2)
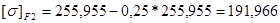 (Н/мм2)
(Н/мм2)
Принимаем 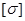 F = 191,966 (Н/мм2), т.к. выбираем по менее прочным зубьям.
F = 191,966 (Н/мм2), т.к. выбираем по менее прочным зубьям.
3.12 Составляем табличный ответ расчета:
| Элемент передачи | Марка стали | Термообработка | НВср | [s]H, Н/мм2 | [s]F, Н/мм2 |
| Шестерня | 40Х | Улучшение | 285,5 | 580,9 | 220,549 |
| Колесо | 40Х | Улучшение | 248,5 | 514,3 | 191,966 |
4. Расчет зубчатой передачи
4.1 Проектный расчет
4.1.1 Определяем межосевое расстояние передачи:
 (мм)
(мм)
где
Ka - вспомогательный коэффициент, для косозубой передачи, принимаем равный 43
UЗП - передаточное число закрытой передачи, равное 5,0
Т2 - вращающий момент на тихоходном валу редуктора, Н*м
yа - коэффициент ширины венца колеса, равное 0,315
[s]н - допускаемое контактное напряжение, H/мм2
Kнb - коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся колес, равный 1
Принимаем:  (мм)
(мм)
4.1.2 Определяем делительный диаметр колеса:
 (мм)
(мм)
где
aw = 102(мм) - межосевое расстояние передачи
UЗП = 5,0 - передаточное число передачи
4.1.3 Определяем ширину венца колеса: b2 = шa* aw = 0,315*102 = 32,13(мм) где
шa = 0,315 - коэффициент ширины венца колеса
aw = 102(мм) - межосевое расстояние передачи
4.1.4 Определяем модуль зацепления:
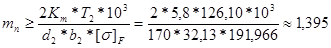 (мм)
(мм)
где
Km - вспомогательный коэффициент для косозубых передач, равный 5,8
Т2 - вращающий момент на тихоходном валу редуктора, Н*м
Принимаем: mn=1,5(мм)
4.1.5 Определяем угол наклона зубьев для косозубых передач:

4.1.6 Определяем суммарное число зубьев шестерни и колеса:
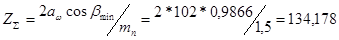 (зубьев)
(зубьев)
где
aw - межосевое расстояние передачи, мм
mn - нормальный модуль зацепления, мм
bmin - угол наклона зубьев
4.1.7 Уточняем фактический угол наклона зубьев:

4.1.8 Определяем число зубьев шестерни:
 (зубьев)
(зубьев)
4.1.9 Определяем число зубьев колеса:
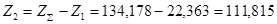 (зубьев)
(зубьев)
4.1.10 Определяем фактическое передаточное число передачи и проверяем его отклонение от заданного:
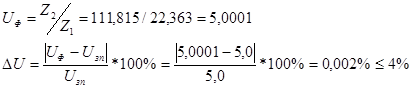
4.1.11 Определяем фактическое межосевое расстояние передачи:
 (мм)
(мм)
4.1.12 Определяем основные геометрические параметры передачи:
а) Определяем делительный диаметр шестерни и колеса:
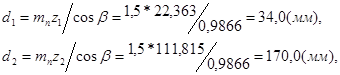
где
mn - нормальный модуль зацепления, мм
Z1 - число зубьев шестерни
Z2 - число зубьев колеса
b - угол наклона зубьев
б) Определяем диаметр вершин зубьев шестерни и колеса:

где
d1 - делительный диаметр шестерни, мм
d2 - делительный диаметр колеса, мм
mn - нормальный модуль зацепления, мм
в) Определяем диаметр впадин зубьев шестерни и колеса:
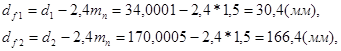
где
d1 - делительный диаметр шестерни, мм
d2 - делительный диаметр колеса, мм
mn - нормальный модуль зацепления, мм
г) Определяем ширину венца шестерни и колеса:
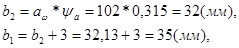
где
aw - межосевое расстояние передачи, мм
yа - коэффициент ширины венца колеса, равен 0,315
4.2 Проверочный расчет
4.2.1 Проверяем межосевое расстояние передачи aw, мм:

где
d1 - делительный диаметр шестерни, мм
d2 - делительный диаметр колеса, мм
aw - межосевое расстояние передачи, мм
4.2.2 Определяем окружную силу в зацеплении Ft, H:
 (Н)
(Н)
где
d2 - делительный диаметр колеса, мм
Т2 - вращающий момент на тихоходном валу редуктора, Н*м
4.2.3 Определяем окружную скорость колеса передачи V 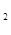 , м / с:
, м / с:
V2 = 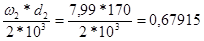 (м/с)
(м/с)
где
w2 - угловая скорость тихоходного вала,рад/с
d2 - делительный диаметр колеса, мм
4.2.3 Определим значение коэффициента, учитывающего распределение нагрузки между зубьями, KНa = 1,125
4.2.4 Определяем значение коэффициента динамической нагрузки, КНu:
КНu = 1,01
4.2.5 Определяем значение коэффициента неравномерности нагрузки по длине зуба, КНb:
шб=  ; КНb=1,1
; КНb=1,1
4.2.7 Проверяем контактное напряжение [у]н, (Н/мм2):
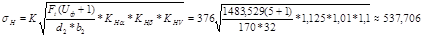 £ 514,3(Н/мм2),
£ 514,3(Н/мм2),
где
K - вспомогательный коэффициент равный 376
Uф = 5,0 - фактическое передаточное число
d2 - делительный диаметр колеса, мм
в2 - ширина венца колеса, мм
4.2.8 Определяем эквивалентные числа зубьев, шестерни и колеса:
Zv1 = 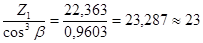 ; Zv2 =
; Zv2 = 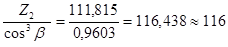
где
Zv1 = 23 – число зубьев шестерни
Zv2 = 116 – число зубьев колеса
в = 9,40
4.2.9 Определяем коэффициент формы зуба шестерни YF1 и колеса YF2:
YF1 = 3,93
YF2 = 3,61
4.2.10 Определяем значение коэффициента распределения нагрузки между зубьями KF2:
KF2= 0,91
4.2.11 Определяем значение коэффициента неравномерности нагрузки KFв:
KFв= 1,095
4.2.12 Определяем значение коэффициента динамической нагрузки KFV:= 1,03
4.2.13 Определяем значение коэффициента наклона зуба Yв:
Yв= 1 - 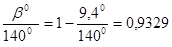
где
в= 9,40 - угол наклона зуба.
4.2.14 Проверяем напряжение изгиба зубьев шестерни и колеса:
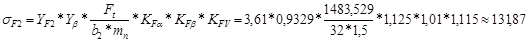
131,87 £ 191,97(Н/мм2)


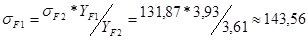 £ 220,55(Н/мм2)
£ 220,55(Н/мм2)

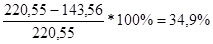
где
[у]F1 = 220,55(Н/мм2) - допускаемое напряжение изгиба зубьев шестерни
[у]F2 = 191,97(Н/мм2) – допускаемое напряжение изгиба зубьев колеса
4.2.15 Составляем табличный ответ расчета
| Проектный расчет | |||||||
| Параметр | Значение | Параметр | Значение | ||||
| Межосевое расстояние аw, мм | Угол наклона зубьев b | 9,40 | |||||
| Модуль зацепления, m | 1,5 | ||||||
| Ширина зубчатого венца: | Диаметр делительной окружности: | ||||||
| шестерни b1, мм | шестерни d1, мм | 34,0 | |||||
| колеса b2, мм | колеса d2, мм | 170,0 | |||||
| Число зубьев: | Диаметр окружности вершин: | ||||||
| шестерни Z1 | 22,363 | шестерни dа1, мм | 37,0 | ||||
| колеса Z2 | 111,815 | колеса dа2, мм | 173,0 | ||||
| Вид зубьев | Косые | Диаметр окружности впадин: шестерни df1, мм колеса df2, мм | 30,4 166,4 | ||||
| Проверочный расчет | |||||||
| Параметр | Допускаемые значения | Расчетные значения | Примечания | ||||
| Контактные напряжения sН, Н/мм2 | 514,3 | 1,63% | |||||
| Напряжения изгиба, Н/мм 2 | sF1 | 220,55 | 143,56 | 34,9% | |||
| sF2 | 191,97 | 131,87 | 31,3% | ||||