Пирамида, формула вычисления объёма пирамиды
Вычислить объём тела – это значит сравнить его с эталоном, например с кубическим сантиметром. Сравнение происходит с помощью формул.
Пирамида – это геометрическая фигура, которая состоит из многоугольника, точки, не лежащей в плоскости многоугольника и всех отрезков, соединяющих эту точку с точками многоугольника.
На рисунке 1 изображена пирамида SABCD. Точка S не лежит в плоскости основания (многоугольника ABCD) и соединена с вершинами многоугольника. Перпендикуляр SH – высота пирамиды.
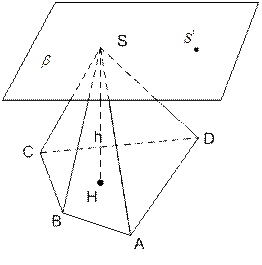
Рис. 1. Пирамида
Формула для вычисления объёма пирамиды:
 , где S – площадь основания пирамиды (ABCD), h – высота пирамиды (
, где S – площадь основания пирамиды (ABCD), h – высота пирамиды (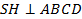 )
)
Если плоскость  , тогда вершину S можно двигать по плоскости β в любом направлении, объём пирамиды при этом не изменится. Фигуры, у которых одинаковые объёмы, называются равновеликими. То есть пирамиды SABCD и
, тогда вершину S можно двигать по плоскости β в любом направлении, объём пирамиды при этом не изменится. Фигуры, у которых одинаковые объёмы, называются равновеликими. То есть пирамиды SABCD и  равновеликие.
равновеликие.

Призма, формула вычисления объёма призмы
Призма – это многогранник, основаниями которого являются равные многоугольники, а боковыми гранями – параллелограммы.
На рисунке 2 изображена наклонная призма. Многогранники  и
и 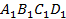 в основаниях лежат в параллельных плоскостях, равны и расположены так, что боковые рёбра (
в основаниях лежат в параллельных плоскостях, равны и расположены так, что боковые рёбра ( ) между собой параллельны.
) между собой параллельны.

Рис. 2. Наклонная призма
Формула для вычисления объёма призмы:
 , где S – площадь основания (
, где S – площадь основания ( или
или 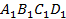 ), h – высота между основаниями, которая получается при опускании перпендикуляра из любой точки основания на плоскость, в которой лежит другое основание этой призмы (
), h – высота между основаниями, которая получается при опускании перпендикуляра из любой точки основания на плоскость, в которой лежит другое основание этой призмы ( ).
).
Если мы рассмотрим пирамиду  , то её объём будет равен:
, то её объём будет равен:
 , где V – объём призмы
, где V – объём призмы 
Задача 1 (нахождение объёма пирамиды)
Дано:  – треугольная призма;
– треугольная призма;  – объём призмы;
– объём призмы; 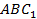 – секущая плоскость (рис. 3).
– секущая плоскость (рис. 3).
Найти: 1.  – объём пирамиды
– объём пирамиды  ; 2.
; 2. 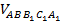 – объём фигуры над секущей плоскостью; 3.
– объём фигуры над секущей плоскостью; 3.  – объём пирамиды
– объём пирамиды  ; 4.
; 4. 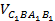 – объём пирамиды
– объём пирамиды 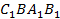
Решение:
1. Найдём объём пирамиды  :
:
 , где
, где  – объём призмы
– объём призмы 
Так как  , то
, то


Рис. 3. Иллюстрация к задаче
2. Для нахождения объёма верхней части из общего объёма вычтем объём нижней части, то есть объём пирамиды  :
:

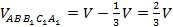
3. Найдём объёмпирамиды  и
и 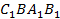 . Для этого рассмотрим боковую грань призмы
. Для этого рассмотрим боковую грань призмы  .Это параллелограмм, следовательно, площадь треугольника
.Это параллелограмм, следовательно, площадь треугольника  равна площади треугольника
равна площади треугольника  . А так как эти треугольники являются основаниями пирамид
. А так как эти треугольники являются основаниями пирамид  и
и 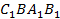 , то такие пирамиды равновеликие, то есть их объёмы равны и в сумме дают объём верхней части
, то такие пирамиды равновеликие, то есть их объёмы равны и в сумме дают объём верхней части  .
.


Ответ: 1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 
Задача 2 (нахождение объёма многогранника с помощью формулы объёма пирамиды)
Дана правильная треугольная призма  (рис. 4), площадь основания которой равна 6, а боковое ребро равно 8. Найдите объём многогранника, вершинами которого являются точки
(рис. 4), площадь основания которой равна 6, а боковое ребро равно 8. Найдите объём многогранника, вершинами которого являются точки  .
.
Дано: 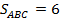 ;
;  ;
; 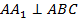 ;
;  – секущая плоскость.
– секущая плоскость.
Найти: 
Решение:
Секущая плоскость делит призму на две фигуры.
1. Найдём объём призмы  .
.
 ,
,  – площадь основания призмы,
– площадь основания призмы, 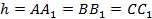 – высота призмы
– высота призмы
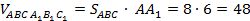

Рис. 4. Иллюстрация к задаче
2. Найдём объём пирамиды 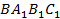 , то есть части призмы, находящейся над секущей плоскостью
, то есть части призмы, находящейся над секущей плоскостью  .
.
 , где
, где  – основание пирамиды,
– основание пирамиды,  – высота пирамиды
– высота пирамиды

3. Искомый нами объём – это объём фигуры  , которая находится под секущей плоскостью
, которая находится под секущей плоскостью  , следовательно, её объём равен:
, следовательно, её объём равен:


Ответ: 
Задача 3 (нахождение объёма пирамиды)
Стороны оснований правильной усечённой треугольной пирамиды равны  и
и  , высота пирамиды равна 4. Найти объём данной пирамиды.
, высота пирамиды равна 4. Найти объём данной пирамиды.
Дано:  ;
;  ;
;  (рис. 5).
(рис. 5).
Найти: 
Решение:
Вспомним формулу вычисления объёма усечённой пирамиды:
1.  , где
, где  – высота усечённой пирамиды,
– высота усечённой пирамиды,  – площадь нижнего основания (
– площадь нижнего основания ( ),
),  – площадь верхнего основания (
– площадь верхнего основания (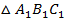 ).
).

Рис. 5. Иллюстрация к задаче
2. Дана правильная усечённая пирамида, следовательно, в основаниях лежат равносторонние треугольники. Площадь равностороннего треугольника равна:
 , где a – длина стороны треугольника
, где a – длина стороны треугольника
Площадь нижнего основания:

Площадь верхнего основания:

3. Подставляем известные значения в формулу объёма усечённой пирамиды:


Ответ: