Отношение. Проценты.
Отношение двух чисел - это частное от деления одного из них на другое.
Отношение показывает, во сколько раз первое число больше второго или какую часть первое число составляет от второго.
Например, в коллекции монет золотые к серебряным в отношении 8: 5,
т.е. 8х – золотых монет и 5х – серебряных монет!!!
Пропорция - это равенство двух отношений. В пропорции различают крайние и средние члены.
8 и 5 называют крайними членами; 4 и 10 - средние члены.
Основное свойство: произведение крайних членов пропорции равно произведению средних.
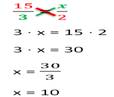Правило (креста) "X": нарисуем карандашом поверх знака равенства крест. Чтобы найти "x", используем основное свойство пропорции.
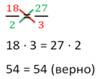
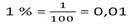Проценты.
Процент - это одна сотая часть от числа.
Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак %.
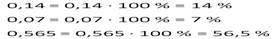
Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
Задача-образец.
В магазин электротоваров привезли лампочки. Среди них оказалось 16 разбитых лампочек, что составило 2% их числа. Сколько лампочек привезли в магазин?
Решение.
Важно!!! Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д.
Краткая запись:
Разбиты – 16 ламп. – 2%
Привезли – х ламп. – 100%
Используя таблицу, составим нужную пропорцию и решим её с помощью правила "креста".
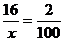, то х = 16 ∙ 100:2, х = 800. Ответ: 800 лампочек.
Действия с десятичными дробями.
При сложении (вычитании) десятичных дробей надо:
1) при необходимости уравнять количество знаков после запятой, добавляя нули к соответствующей дроби,
2) записать дроби так, чтобы их запятые находились друг под другом,
3) сложить (вычесть), не обращая внимания на запятую,
4) поставить запятую в сумме (разности) под запятыми, складываемых (вычитаемых) дробей.
При умножении десятичной дроби на натуральное число ,надо:
1) перемножить числа, не обращая внимания на запятую;
2) в полученном произведении поставить запятую так, чтобы справа от нее было столько же цифр, сколько в десятичной дроби.
При умножении десятичной дроби на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей стоит в множителе.
0,065 • 1000 = 0065, = 65; 3,12 • 10 = 31,20 = 31,2; 3,12 • 100 = 312,00 = 312. Умножение двух десятичных дробей выполняется так:
1) числа перемножаются без учета запятых;
2) запятая в произведении ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых. Например:
1,1 • 0,2 = 0,22; 1,1 • 1,1 = 1,21; 2,2 • 0,1 = 0,22.
Вместо умножения любого числа на 0,1; 0,01; 0,001, можно разделить это число на 10; 100; 1000 и т.д. 22 • 0,1 = 22: 10 = 2,2.
Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.
При делении десятичной дроби на 10, 100, 1000 и т.д. надо перенести запятую в этой дроби влево настолько же знаков, сколько нулей в делителе.
34,9: 10 = 3,49; 746: 100 = 7,46; 28,1: 1000 = 0,0281.
При делении на десятичную дробь, сначала переносим запятую в делимом и делителе вправо на столько знаков, сколько их после запятой в делителе. А затем выполняем деление на натуральное число.
543,96: 0,3 = 5439,6: 3 = 1813,2; 237: 0,03 =23700: 3 = 7900; 7,44: 0,4 = 744:40
Если целая часть десятичной дроби меньше, чем делитель, то в частном сразу ставим 0 в целой части.
Разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д. - то же самое, что умножить её на 10, 100, 1000 и т.д.
7,1: 0,1 = 7,1 • 10 = 71 25,37: 0,001 = 25,37 • 1 000 = 25 370 0,08: 0,1 = 0,08 • 10 =0,8