Пирамида.
Правильная и усеченная пирамида.
Площадь поверхности и объем пирамиды.
I. 
Пирамида. Правильная пирамида.
Пирамидой называется многогранник, состоящий из плоского многоугольника — основания пирамиды, точки, не лежащей в плоскости основания,— вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 1).
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Поверхность пирамиды состоит из основания (плоский многоульник) и боковых граней. Каждая боковая грань — треугольник. Рис.1
S
Общая вершина боковых граней является вершиной пирамиды.
Высотой пирамиды (h)называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Треугольная пирамида называется также тетраэдром.
Вид пирамиды определяется п-угольником, лежащем в ее основании.
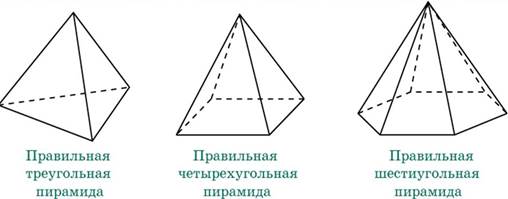Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
В основании правильные многоугольники:
равносторонний квадрат правильный
треугольник шестиугольник
· Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
· Боковые ребра правильной пирамиды являются равными равнобедренными треугольниками.
· 
Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.
Осью (SO ) правильной пирамиды называется прямая, содержащая ее высоту.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой (SK).
II. Усеченная пирамида.
Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Вторая часть пирамиды — это многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды есть подобные (более того) многоугольники, боковые грани — трапеции.
Усеченная пирамида, полученная из правильной, также называется правильной. Боковые грани правильной усеченной пирамиды — равные равнобокие трапеции; их высоты называются апофемами.
Основания усеченной пирамиды — подобные многоугольники.
A1B1, A2B2, … AnBn - усеченная пирамида (см. рисунок).
Отрезки A1B1, A2B2, … AnBn называют боковыми ребрами усеченной пирамиды.
A1A2...An - нижнее основание, а В1В2...Вn – верхнее основание.
A1B1B4 A4, A4B4B3 A3, … – называются боковыми гранями и являются трапециями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды (HH1 и В1O).
Свойства правильной усеченной пирамиды:
- Боковые грани равны;
- Боковые ребра равны;
- Апофемы равны;
- Двугранные углы при каждом основании равны;
- Боковые углы при боковых ребрах равны.
III. Площадь поверхности и объем пирамиды и усеченной пирамиде.
Площадь поверхности и объем пирамиды.
Площадью полной поверхности пирамиды называются сумма площади основания и площадей всех ее граней.
Sполн = Sбок + Sосн
Площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
– площади боковых граней; n – количество граней.
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
– полупериметр основания; l – апофема.
Для вычисления площади боковой поверхности правильной пирамиды существуют еще одна формула:
где P — периметр основания, h — апофема,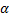 
— двугранный угол при основании.
Объём пирамиды вычисляется по формуле V= 
×Sосн⋅H,
где H — высота пирамиды.
Обрати внимание!
Не путай l — апофему с H — высотой пирамиды!