Алгоритм исключения Гаусса
Рассмотрим один из самых распространенных методов решения систем линейных алгебраических уравнений – метод Гаусса (метод последовательного исключения неизвестных). Он состоит из двух основных этапов: прямой ход и обратный ход.
Простейший вариант метода: схема единственного деления.
Будем считать, что элемент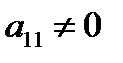 
. Будем называть его главным элементом первого шага.
Найдем множители первого шага 
. Вычтем последовательно из второго, третьего, 
-го уравнения первое умноженное на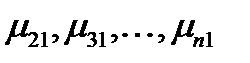 
. Это позволит исключить из этих уравнений неизвестное 
.
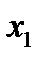В результате получим эквивалентную систему
,
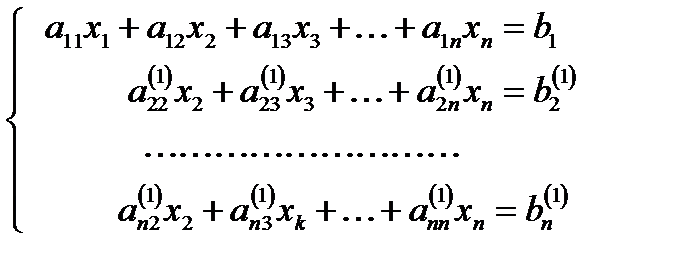где 
, 
.
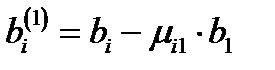На следующем шаге из всех уравнений, начиная с третьего, исключается неизвестное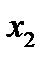 
.
После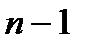 
-го шага получаем систему с верхней диагональной матрицей
.
После этого переходим к обратному ходу: из последнего уравнения находим неизвестное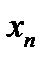 
, подставляя его в предпоследнее уравнение, находим 
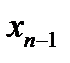и т.д. до первого уравнения.
Заметим, что если один из главных элементов окажется равным нулю, то деление станет невозможным. Но даже если главный элемент близок к нулю это приводит к неконтролируемому росту погрешности, т.к. если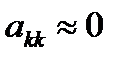 
, то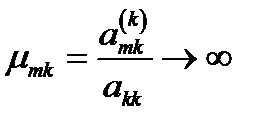 
.
Чтобы избежать этого, каждый цикл всегда начинают с перестановки строк. Среди элементов столбца 
находят главный (наибольший по модулю в 
-м столбце) и перестановкой строк приводят его на главную диагональ. Это схема с выбором главного элемента по столбцам.
Как правило, выбор главного элемента во всей матрице не сильно улучшает погрешность, но заметно усложняет расчет.
Число арифметических операций в методе Гаусса для системы 
составляет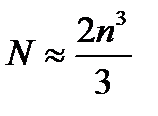 
.
Оценка погрешности и уточнение корня
|
|
Оценить близость какого-либо вектора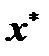 
к решению системы уравнений можно, оценив вектор невязок 
. При этом чаще рассматривается его норма.
Решение систем с несколькими правыми частями. 
- разложение
Рассмотрим, какими преобразованиями матрицы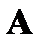 
сопровождается метод Гаусса.
Введя обозначения 
и 
, получим что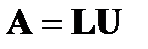 
.
Это и есть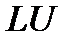 
-разложение матрицы 
.
Теорема 1. Если все главные миноры матрицы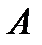 
отличны от нуля, то существуют единственные нижняя треугольная матрица 
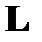и верхняя треугольная матрица 
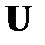такие, что 
.
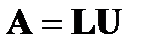Довольно часто на практике случаются ситуации, когда нужно решить несколько систем уравнений с одной матрицей 
и различными правыми частями.
В этом случае разумно провести преобразования, которые повторяются при каждом решении, один раз, и использовать их для различных правых частей.
− разложение дает очень большое преимущество в решении систем уравнений. При нахождении 
− разложения совершенно не использовался вектор правых частей.
Далее получим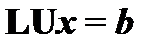 
, обозначим 
, тогда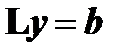 
.
В случае использования метода Гаусса с выбором главного элемента, полученные матрицы не являются 
− разложением матрицы 
. Однако прямой ход по-прежнему равносилен 
− разложению, но не самой матрицы , а матрицы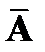 
, полученной из соответствующей перестановкой строк.
Разложение Холецкого (метод квадратных корней)
Используется для симметричной положительно определенной матрицы . Такие матрицы часто встречаются в приложениях (задачи оптимизации, механика твердого тела, теория упругости, уравнения математической физики).
Квадратная матрица называется положительно определенной, если для любого ненулевого вектора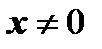 
, выполняется 
.
|
|
Для выяснения положительной определенности матрицы можно проверить одно из условий:
· Все определители угловых миноров матрицы положительны.
· Все собственные значения матрицы положительны.
В основе метода лежит алгоритм построения специального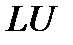 
− разложения матрицы 
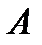, в результате чего она приводится к виду 
.
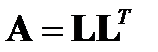Записав матрицу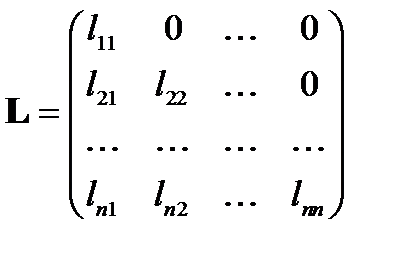 
и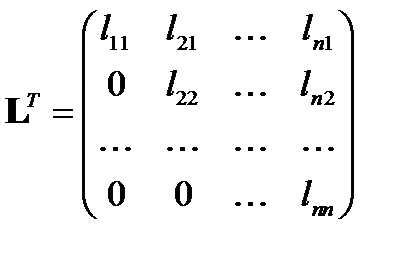 
, перемножим их и приравняем соответствующим элементам матрицы .
, 
, 
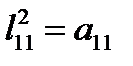
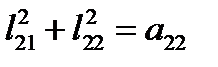
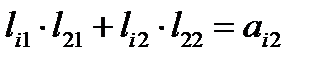Решая систему, последовательно находим
, 
, 
.
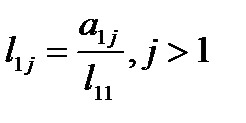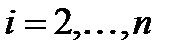
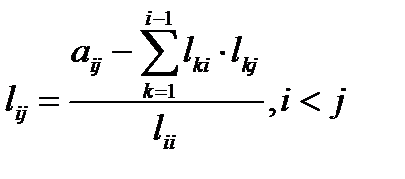Если разложение получено, то решение сводится к последовательному решению двух систем с треугольными матрицам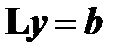и: 
и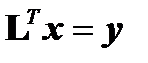 
.
Решение требует порядка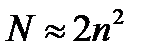 
Этот метод обладает рядом ценных качеств, которые позволяют предпочесть его методу Гаусса:
· При больших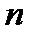 
этот метод требует вдвое меньших вычислительных затрат.
· Безусловным достоинством метода Холецкого является его гарантированная устойчивость.