Двойным интегралом функции f(x,y) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n
6 .Векторное поле: Ротор, Дивергенция, Потенциальное поле, Соленоидальное поле.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
Ротор -вектор вокруг которого закрученность векторных линий максимальна.
Дивергенция -это характеристика наличия в каждой точке источников.
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат.
Соленоидальное поле - это поле в котором Дивергенция в каждой точке равна нулю.
7. Определения ряда. Суммы ряда.
Числовой ряд (или просто рядом) называется выражение вида 
= 
Где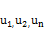 
,… действительные или комплексные числа, называемые членами ряда, 
-общим членом ряда.
Сумма ряда –Если существует конечный предел S=lim 
последовательность частичных сумм ряда, то это предел называют суммой ряда и говорят,что ряд сходится.
8.Необходимый признак сходимости ряда – если ряд сходится то его обший член стримится к нулю.
9. Достаточный признак сходимости Даламбера знакоположительного ряда
Знакоположительным называется такой числовой ряд, все члены которого положительны.
Признак Даламбера.
Если для ряда с положительными членами
существует предел отношения последующего члена к предыдущему
,
то этот ряд сходится при 
и расходится при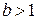 
.
При 
возможны оба случая, т.е. исследование такого ряда по признаку Даламбера не дает однозначного ответа на вопрос о сходимости.
10.Степенной ряд-это частный случай функциональных рядов, в которых члены ряда представляют собой степенные функции аргумента х.
Радиусом сходимости степенного ряда называют такое число (R),при котором ряд сходится если │x│< R,и расходится, если │х│>R.
Интервалом сходимости называют такой интервал от –R до +R,что для всякой точке х, лежащих внутри этого интервала ряд сходится абсолютно, а для точек лежащих вне его, ряд расходится.
11.Ряды Тейлора и Маклорена.
Если функция 
в некотором интервале раскладывается в степенной ряд по степеням 
, то это разложение единственно и задается формулой:
Если в ряде Тейлора положить а=0,то получем разложение функции по степеням х в так называемый ряд Маклорена:
12. Разожение функций sinx,cosx, 
13. Вероятностью события а называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу
Геометрической вероятностью события А называют отношение меры области, благоприятствующей появлению события А, к мере всей области.
14. Теорема умножения вероятностей. Если события 
и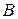 
независимы (т.е. вероятность одного из событий не зависит от появления или непоявления другого), то вероятность произведения событий равна произведению их вероятностей:
.
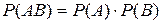Теорема сложения вероятностей. Если события и 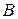несовместны, то вероятность их суммы равна сумме их вероятностей:
.
15. Последовательность 
независимых испытаний, в каждом из которых может произойти некоторое событие (его называют успехом) с вероятностью 
, постоянной при любом испытании, или противоположное ему событие 
(его называют неудачей) с вероятностью 
, называется схемой Бернулли.
Если производится независимых испытаний, в каждом из которых вероятность появления события постоянна и равна 
, то вероятность того, что событие произойдет ровно 
раз определяется формулой Бернулли:
, (5)
где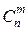 
– число сочетаний из элементов по элементам, которое вычисляется по формуле:
.
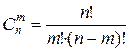16. Выборка - называется совокупность случайно отобранных обьектов.
Средние величины -характеризуют значение признака,вокруг которого проводятся исследования.
Дисперсия -характеризует степень рассеяния индивидуальных значений признака в совокупности от среднего значения.
Среднее квадратичное отклонения показывает на сколько в среднем отклоняется конкретный вариант признака от среднего значения.
17. Случайная величина- это величина которая в результате эксперемента принимает из множества значений только одно случайное значение.
Закон распределения случайной величины это соответствие между возможным значением случайной величины и ее вероятностями.