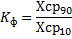Какую строку в таблице выбирать для исследования?
Нужно найти Xср.вз., но не по обычным законам среднего арифметического, а с помощью взвешенных показателей. То есть, нужно использовать так же показатель f – частость (количество единиц в определенном интервале: число работников со стажем от 2 до 5 лет; кол-во регионов с числом школ от 2000 до 3000; кол-во магазинов со средней ценой на молоко от 30 до 40 рублей и т.д.)
В итоге, нам нужно рассчитать общую сумму показателей: f (∑f); и сумму взвешенного показателя:(∑(f*Х)). Затем нужно разделить сумму взвешенного на общую сумму количественных показателей:
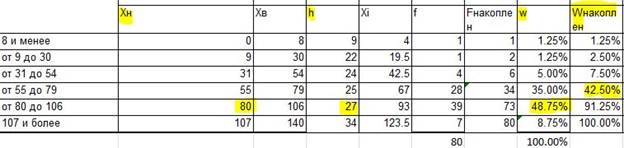
Xср.вз. = ∑ (f*Xi)/∑ (f), где Xi –среднее по Хв и Хн
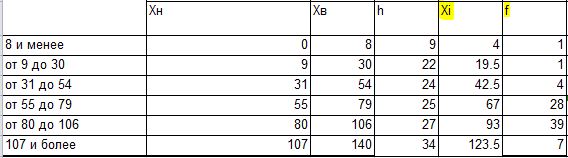
По показателям, данным в таблице, мы увидим, что Хср.вз = 82, данный показатель входит в интервал от 80 до 106, что означает, что эта строка нам и потребуется.
Как рассчитать моду?
Когда мы выбрали строку для исследования, мы можем рассчитать моду:
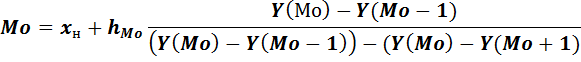
Где hMo определяется показателем h по строке моды,
Y – Частость или плотность (если интервалы X равные – частость, если нет – плотность)
А +1 и -1 – обозначения последующей или предыдущей строки
Частость задается условием, а вот плотность придется вычислять по формуле: f/h
Расчет основных абсолютных статистических показателей:
Как рассчитать медиану?
Строку выберем ту же, что и для моды
Для расчета медианы нам также потребуются показатели доли и накопленной доли
Для того чтобы найти долю, нам потребуется разделить показатель частости f на сумму показателей f: fi/∑fi. Проделав данную операцию для каждой строки, вы найдете долю каждого интервала. Доля обозначается ω. Обратите внимание, что сумма долей должна равняться 100%, если это не так, то отнимите или прибавьте нужные проценты к показателям, желательно сделать это равномерно (учитывая, что для доли, равной 1% прибавление 0,5% исказит показания, поэтому желательно прибавить ошибку расчета к показателю с большей долей). Затем рассчитаем накопленную долю: в первой строке накопленная доля равна доле, накопленная доля следующей равна сумме доли предыдущей и нынешней, третьей – равна доле двух предыдущих и нынешней и так далее:
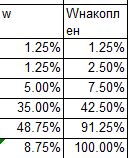
Теперь мы можем приступить собственно к расчету медианы:
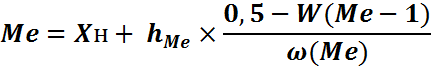
В данном примере медиана равна 84,15. Не забываем, что подставляем мы не проценты, а значения (42,5% = 0,425)
Как рассчитать коэффициент дифференциации?
Прежде чем мы начнем расчеты, нужно понять, что именно представляет собой данный коэффициент. Он показывает отношение максимально загруженной области к минимально загруженной (отношение богатых к бедным, оснащенных к мало оснащённым, опытных к малоопытным).
Формула расчета децилей такая же, как и для медианы, только используем мы вместо значения 0,5 – 0,1 и 0,9 для L1 и L9 соответственно. Обозначение разделения на 10 весьма условно, так как ищем мы показатели по накопленной частости, нам просто нужно найти предпоследнюю строку, и вести расчеты на её основе (или строку, где накопленная частость приближенно равна 90%). L1 находим соответственно по ≈ 10%.
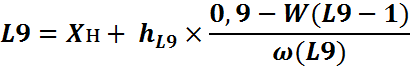
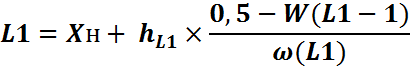
Затем найдем собственно K=L9/L1
В данном примере найденные показатели равны:

В случае, когда данные не сгруппированы (идут сплошной строкой, без интервалов) используем коэффициент Фонда. Среднее по 90% делим среднее по 10%.