Наблюдения называют прямыми в случае, когда результатом этих наблюдений или измерений является сама искомая величина. В случае, когда наблюдаемые величины являются исходными данными для вычисления других параметров, зависящих от этих величин, то к таким наблюдениям применяют термин косвенные наблюдения.
Однако между прямыми и косвенными наблюдениями нет четкой границы. Приведем простой пример. Допустим, что нам нужно знать площадь прямоугольника. В нашем распоряжении есть линейка с нанесенной на ней линейной шкалой. Мы можем с помощью этой линейки измерить стороны и вычислить искомую площадь. Результатом измерений является численное значение площади. Будут ли измерения прямыми, если для вычисления площади приходится перемножать данные измерения? Хочется сказать, что нет, т.к. в данном случае непосредственно площадь не измеряется, а вычисляется. Если бы измерения были выполнены с помощью планиметра, то они были бы прямыми.
С другой стороны, длина отрезка прямой определяется как разность двух отсчетов по линейке. Можно ли такую математическую операцию как вычитание не принимать во внимание и считать измерения сторон прямыми, а перемножение результатом косвенных наблюдений? Условность границы между понятиями прямые и косвенные наблюдения очевидна.
По-видимому, прямыми измерениями можно назвать такие измерения, которые можно неоднократно повторить, и результаты которых могут быть использованы при вычислениях других величин, функционально связанных с результатами прямых измерений. Повторение измерений необходимо для того, чтобы образовать ряд наблюдений для применения статистических методов обработки.
|
|
Некоторая условность в разделении этих двух типов наблюдений (измерений) никак не мешает применению статистических методов оценивания искомых величин, т.к. наблюдения, которые называют косвенными, объединяют оба вида измерений, а прямые измерения можно считать частным случаем косвенных.
Оцениванием называют процедуру определения оценки - приближенной величины - искомого параметра. Для оценивания, например, параметра 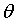 по ряду наблюдений
по ряду наблюдений 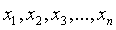 необходимо выполнить вычисления, используя эти наблюдательные данные. Запишем эту процедуру следующим образом:
необходимо выполнить вычисления, используя эти наблюдательные данные. Запишем эту процедуру следующим образом: 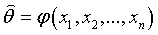 .
.
Функцию 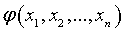 называют статистикой, крышка над
называют статистикой, крышка над 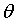 - обозначением параметра будет обозначать оценку.
- обозначением параметра будет обозначать оценку.
Оценку называют несмещенной, если она не содержит систематической ошибки, т.е. 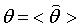 , где треугольные скобки, как и прежде, обозначают осреднение по «бесконечному ансамблю реализаций».
, где треугольные скобки, как и прежде, обозначают осреднение по «бесконечному ансамблю реализаций».
Как правило, несмещенная оценка не единственная, их может быть бесконечное множество. Возникает задача выбора наилучшей из этих оценок. Кажется естественным отобрать ту из них, которая имеет минимальную дисперсию погрешности
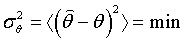 . .
|
3.1. Линейная оценка параметра
Рассмотрим следующую задачу. Требуется определить наилучшую в среднеквадратическом смысле оценку параметра Х, значения которого заданы рядом прямых наблюдений 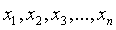 . Линейной оценкой параметр Х будет равен линейной статистике
. Линейной оценкой параметр Х будет равен линейной статистике 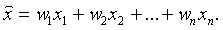
Эта оценка будет несмещенной, если 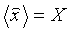 или
или 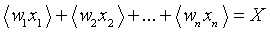 .
.
Поскольку 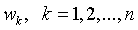 - точные константы, их можно вынести за скобки осреднения
- точные константы, их можно вынести за скобки осреднения  .
.
Примем гипотезу о случайности погрешностей измерений. Если 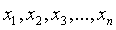 содержат лишь случайную ошибку, то средние их значения равны точному, т.е.
содержат лишь случайную ошибку, то средние их значения равны точному, т.е.  .
.
|
|
Теперь условие несмещенности принимает вид 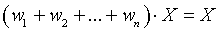 , или при
, или при 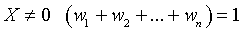 .
.
Это и есть условие несмещенности линейной оценки. Таким образом, имеем одно уравнение для определения n неизвестных. Число решений - бесконечно, вернее 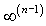 , где (n-1) - число степеней свободы выбора коэффициентов. Действительно, если (n - 1) коэффициентам
, где (n-1) - число степеней свободы выбора коэффициентов. Действительно, если (n - 1) коэффициентам 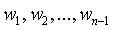 задать любые произвольные значения, то последний коэффициент определится однозначно
задать любые произвольные значения, то последний коэффициент определится однозначно 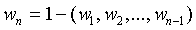 .
.
Воспользуемся вторым условием - минимума дисперсии погрешности оценки. Рассмотрим два случая.
3.1.1. Независимые и равноточные наблюдения
В этом случае дисперсии ошибок всех наблюдений равны 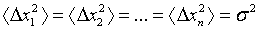 .
.
Для независимых наблюдений дисперсия суммы равна сумме дисперсий. Поэтому 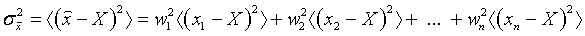 .
.
Вследствие равноточности имеем 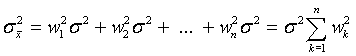 .
.
Нужно найти минимум функции 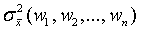 при условии, что
при условии, что 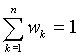
Поступим следующим образом. Определим 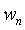 через остальные коэффициенты и подставим в выражение для дисперсии
через остальные коэффициенты и подставим в выражение для дисперсии 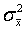
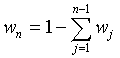 , , 
|
Теперь задачу можно решить как задачу поиска абсолютного минимума: 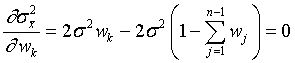 .
.
Отсюда 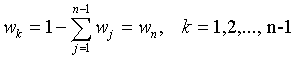 .
.
Итак, все коэффициенты равны одному и тому же числу. Легко понять, что это число 1/n. Таким образом, 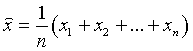 .
.
Вывод: арифметическое среднее есть несмещенная и наилучшая в среднеквадратическом смысле оценка величины, полученная по равноточным и независимым наблюдениям.
3.1.2. Независимые и неравноточные наблюдения
Теперь будем считать, что каждое наблюдение 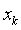 содержит погрешности, дисперсии которых не обязательно равны. Пусть
содержит погрешности, дисперсии которых не обязательно равны. Пусть 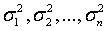 соответственно дисперсии погрешностей
соответственно дисперсии погрешностей 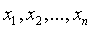 . Теперь дисперсия линейной оценки будет равна
. Теперь дисперсия линейной оценки будет равна 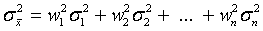 .
.
Определим минимум 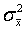 при условии, что
при условии, что 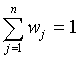 . Поступим по аналогии с предыдущими рассуждениями:
. Поступим по аналогии с предыдущими рассуждениями:
|
|
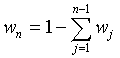 , , 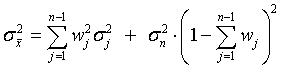 , , 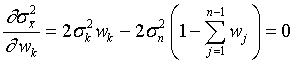
|
Поскольку 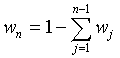 , то получим уравнение
, то получим уравнение 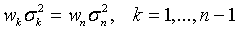 .
.
Полученное равенство говорит о том, что все произведения вида 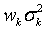 равны между собой и не зависят от индекса k. Кроме того, сумма
равны между собой и не зависят от индекса k. Кроме того, сумма 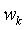 должна равняться единице.
должна равняться единице.
Пусть 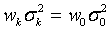 , где
, где 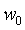 - некоторый нормировочный множитель, а
- некоторый нормировочный множитель, а 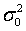 - константа, имеющая размерность дисперсии. Отсюда
- константа, имеющая размерность дисперсии. Отсюда 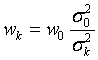 ,
, 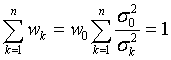 .
.
Обозначим 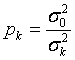 ,
, 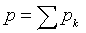 . Теперь определим
. Теперь определим 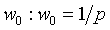 . Итак,
. Итак, 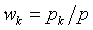 . Наилучшая линейная оценка в этом случае равна
. Наилучшая линейная оценка в этом случае равна 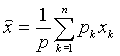 , где
, где 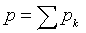 ,
, 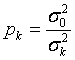 .
.
Величины pk носят название веса наблюдения, ибо формула для определения 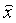 аналогична той, которую применяют для вычисления центра тяжести, если «вес» точки с координатой xk будет равен pk. Постоянная
аналогична той, которую применяют для вычисления центра тяжести, если «вес» точки с координатой xk будет равен pk. Постоянная 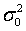 может быть произвольной, так как ее выбор не влияет на оценку
может быть произвольной, так как ее выбор не влияет на оценку 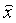 . Ее можно также интерпретировать как дисперсию наблюдения, вес которому мы приписываем равным единице («дисперсия единицы веса»).
. Ее можно также интерпретировать как дисперсию наблюдения, вес которому мы приписываем равным единице («дисперсия единицы веса»).
3.2. Дисперсия ошибок линейных оценок
Получим теперь формулы для дисперсии ошибок линейных оценок. Рассмотрим два варианта: все наблюдения независимы, но они либо равноточны, либо неравноточны.
3.2.1. Независимые и равноточные наблюдения
Поскольку арифметическое среднее - оценка равноточных наблюдений - является несмещенной, то погрешность арифметического среднего равна арифметическому среднему погрешности измерений 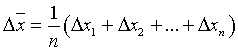 , а дисперсия ошибки среднего арифметического равна
, а дисперсия ошибки среднего арифметического равна 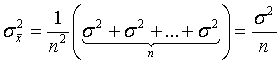 .
.
Таким образом, с увеличением числа наблюдений искомого параметра точность оценки увеличивается, дисперсия ошибки арифметического среднего убывает обратно пропорционально n.
Стандартное отклонение ошибки арифметического среднего 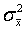 убывает как квадратный корень из
убывает как квадратный корень из 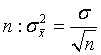 .
.
Отсюда вывод: для того, чтобы увеличить точность оценки на один порядок (в 10 раз), нужно увеличить объем данных на два порядка (в 100 раз) и т.д. Возникает естественно вопрос, можно ли таким способом увеличивать точность беспредельно? Математика на этот вопрос дает утвердительный ответ. Да, можно измерять отрезки прямой с точностью до одного микрометра линейкой с миллиметровыми делениями. Для этого нужно выполнить 1000000 измерений, при этом измерение должно содержать только строго случайные погрешности. Последнее условие, конечно, не выполняется, так как полное отсутствие систематических погрешностей на практике обеспечить нельзя.
3.2.2. Независимые и неравноточные наблюдения
Для оценки параметра Х при неравноточных измерениях мы имеем формулу
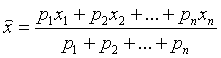 , где , где 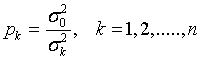
|
Обозначая для краткости 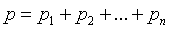 , получим ошибку
, получим ошибку
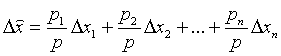
|
Все ошибки  по условию независимы, поэтому
по условию независимы, поэтому
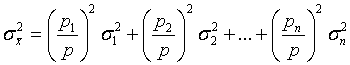
|
Но 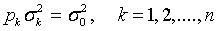 , отсюда
, отсюда
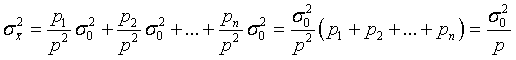
|
Итак, дисперсия ошибки среднего весового равна «дисперсии единицы веса», поделенная на сумму весов наблюдений 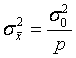 .
.
Учитывая, что дисперсия ошибки каждого наблюдения равна дисперсии единицы веса, деленной на вес этого наблюдения (см. 3.2.1), 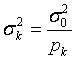 , делаем вывод, что вес среднего весового равен сумме весов наблюдений.
, делаем вывод, что вес среднего весового равен сумме весов наблюдений.
3.3. Оценка дисперсии единицы веса по данным наблюдений
Произвольно взятая константа 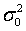 есть не что иное, как дисперсия ошибки наблюдения, которому мы приписываем вес единица. Произвольность этой константы определяется тем, что мы произвольно приписываем вес единица какому-либо реальному или воображаемому наблюдению. В случае равноточных наблюдений обычно вес, равный единице, дают каждому наблюдению. В этом случае
есть не что иное, как дисперсия ошибки наблюдения, которому мы приписываем вес единица. Произвольность этой константы определяется тем, что мы произвольно приписываем вес единица какому-либо реальному или воображаемому наблюдению. В случае равноточных наблюдений обычно вес, равный единице, дают каждому наблюдению. В этом случае 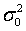 не может быть произвольной величиной. Эта величина не может быть произвольной величиной и в том случае, когда вес наблюдения известен, и выбран обратно пропорционально дисперсии ошибки.
не может быть произвольной величиной. Эта величина не может быть произвольной величиной и в том случае, когда вес наблюдения известен, и выбран обратно пропорционально дисперсии ошибки.
Пусть 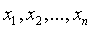 - исходные данные измерений,
- исходные данные измерений, 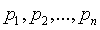 - их веса. Дисперсии ошибок отдельных наблюдений будем считать неизвестными. По определению весов имеем
- их веса. Дисперсии ошибок отдельных наблюдений будем считать неизвестными. По определению весов имеем 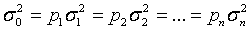 .
.
Очевидно, справедливо равенство 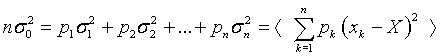 .
.
Следовательно, 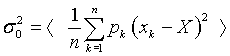 .
.
Таким образом, дисперсия единицы веса равна среднему значению арифметического среднего произведений весов на квадраты погрешностей. Операция, обозначенная треугольными скобками, требует бесконечного повторения набора наблюдений 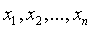 и является лишь теоретической процедурой. Поэтому в качестве оценки дисперсии единицы веса можно принять величину
и является лишь теоретической процедурой. Поэтому в качестве оценки дисперсии единицы веса можно принять величину 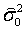 , полученную из единственного ряда наблюдений
, полученную из единственного ряда наблюдений
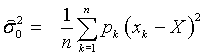
|
Как следует из приведенного равенства для 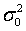 , эта оценка несмещенная
, эта оценка несмещенная 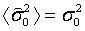 .
.
Для вычисления оценки дисперсии по полученной формуле требуется знать точное значение параметра Х. На практике чаще всего это значение нам неизвестно. Поэтому заменим Х на его оценку 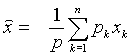 и проверим полученное равенство на несмещенность
и проверим полученное равенство на несмещенность 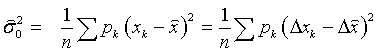 .
.
Здесь и далее суммирование ведется по k от 1 до n. Для краткости пределы суммирования мы будем опускать.
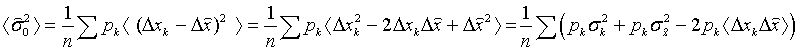
|
Остается определить ковариацию: 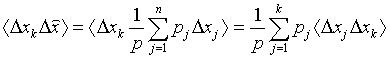 .
.
Вследствие независимости измерений ковариации ошибок с разными индексами равны нулю, а с одинаковыми - дисперсии: 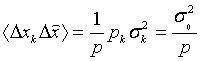
Учитывая, что 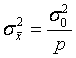 , получим
, получим 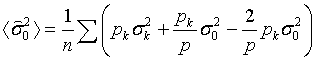 .
.
Таким образом, замена точного значения параметра Х на приближенное 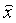 при вычислении оценки дисперсии приводит к тому, что эта оценка оказалась смещенной. Умножая ее на
при вычислении оценки дисперсии приводит к тому, что эта оценка оказалась смещенной. Умножая ее на 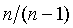 , получим несмещенную оценку дисперсии единицы веса
, получим несмещенную оценку дисперсии единицы веса
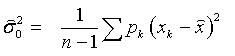
|
Число в знаменателе (n - 1) указывает на то, что наша статистика, принятая для вычисления оценки дисперсии, 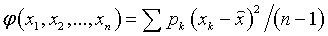 имеет (n - 1) степеней свободы. Одна степень свободы из n потрачена на то, чтобы образовать оценку
имеет (n - 1) степеней свободы. Одна степень свободы из n потрачена на то, чтобы образовать оценку 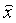 .
.
При равноточных наблюдениях все дисперсии ошибок, а следовательно, и веса наблюдений равны. Пусть pk, тогда 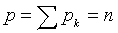 . Получим
. Получим
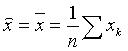 , , 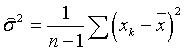
|
Оценку стандартного отклонения для ошибок называют среднеквадратической ошибкой (СКО). Для этой величины, полученной на основании опыта, мы будем применять обозначение 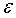 . Таким образом, для равноточных наблюдений имеем,
. Таким образом, для равноточных наблюдений имеем, 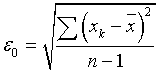 ,
,  для неравноточных наблюдений.
для неравноточных наблюдений.
В случае, когда величина Х известна, то в знаменателях приведенных формул (n -1) нужно заменить на n.
3.4. Выбор весов
Правильный выбор весов наблюдений гарантирует корректность алгоритма определения «наилучшего» значения параметра и его СКО. Однако, величины дисперсий погрешностей каждого отдельного наблюдения, как правило, неизвестны. Тем не менее, в отдельных случаях веса наблюдениям можно назначить совершенно строго.
Например, пусть x1 получено как арифметическое среднее из n1 равноточных измерений, x2 - из n2 таких же измерений и т.д. Тогда, согласно изложенному ранее дисперсии ошибок 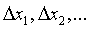 будут соответственно в
будут соответственно в 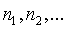 раз меньше, чем дисперсия одиночного измерения. Если функция ошибок одиночного измерения равна
раз меньше, чем дисперсия одиночного измерения. Если функция ошибок одиночного измерения равна 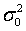 , то
, то  .
.
Легко видеть, что в качестве весов можно взять число рядовых измерений, из которых получили отдельное значение xk. Поскольку веса можно брать с точностью до постоянного множителя, то 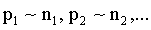 .
.
Второй способ - менее надежный. Он основан на замене дисперсии ошибки n -го наблюдения 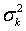 на квадрат его среднеквадратической ошибки
на квадрат его среднеквадратической ошибки 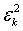 .
.
Недостаток этого метода заключается в том, что квадраты СКО могут значительно отличаться от дисперсий, так как СКО вычисляют, как правило, на основании внутренней сходимости данных при их сравнительно небольшом количестве. Тем не менее, когда ничего другого не остается, полагают