Механическая система – совокупность материальных точек (тел), рассматриваемых как единое целое.
Системы бывают:
a) замкнутые (изолированные), на которые действуют внешние силы (нет взаимодействия с внешней средой);
б) не замкнутые (не изолированные), на которые действуют внешние силы.
Все законы сохранения в основном даются для замкнутых систем.
Законы сохранения импульса – геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
,
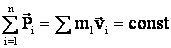где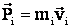 
– импульс тела.
Импульс (количество движения) – мера механического движения. Применение такой меры допустимо, если передача механического движения от одного тела к другому, происходит без превращения в другие формы движения материи.
Механическое движение может переходить в другие виды материи (в тепловое, электромагнитное действие и др.). Переходы осуществляются в строго определенных количествах соотношениях. Общей мерой для всех видов движения материи является энергия.
Энергия – мера количества любых видов движения материи (тела).
Единство материи и движения нашло наиболее общее выражение в формуле Эйнштейна:
∆E = ∆mc²,
где c – скорость света в вакууме,
∆E – изменение энергии.
Эта формула говорит о том, что увеличение или уменьшение энергии (т.е. количества определенной формы движения), всегда происходит с увеличением или уменьшением массы (т.е. количества формы материи).
Поскольку энергия – мера движения, то её можно количественно выразить через параметрическое состояние системы, т.е. энергия – функция состояния.
Работа – мера передачи действия (в частном случае механического) от одного тела к другому в процессе взаимодействия.
|
|
Работа – мера измерения энергии.
Если материальная точка (тело) под действием внешней силы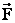 
совершила перемещение 
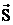, то производится работа A.
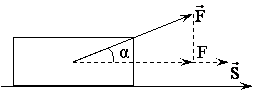
или 
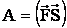
работа равна скалярному произведению силы на перемещение. Работа – скалярная величина.
Из уравнения работы следует:
а) если α = 0, то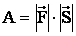 
– максимальна работа совершенная силой направленной вдоль перемещения;
б) если 
, то A > 0 – работа совершается за счёт энергии тела, со стороны которого действует сила;
в) ес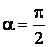ли 
или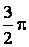 
, то A = 0 – работа совершается за счет энергии движущегося тела против сил сопротивления (в частности сил трения).
Если работа совершается в однородном постоянном силовом поле, то:
- работа по замкнутому пути равна нулю;
- работа не зависит от формы пути, а определяется положением начальной и конечной точек пути.
Мощность – физическая величина, характеризующая скорость работы A:
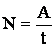
Если сила F = const, то N = F·v, где v – скорость движения.
К механической энергии относят два вида энергии – кинетическую Eк и потенциальную ∆Еп. Чтобы получить выражение энергии в виде функции параметров состояния механического движения, легче это сделать, если учесть, что изменение энергии ∆Е пропорционально работе A:
Выразить работу A =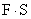 
, где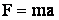 
– действующая сила и перемещение:
,
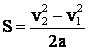где v2 и v1 – конечная и начальная скорость перемещения, получается:
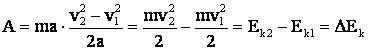
Величина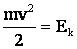 
– называется кинетической энергией тела, а полученный результат для работы силы называют теоремой о кинетической энергии, которая выполняется для сил любой природы, в том числе и для переменных сил.
|
|
Энергия, обусловленная, взаимным расположением тел или частей одного и того же тела и характером их взаимодействия называется потенциальной энергией.
Если материальная точка (тело) перемещается и скорость в начальной и конечной точках траектории равна нулю, значит в результате совершенной работы произошло изменение не кинетической формы энергии, а потенциальной. Изменения потенциальной энергии ∆Еп зависят от относительного изменения взаимного расположения взаимодействующих тел. Потенциальная энергия относится не только к выбранной материальной точек, но и ко всей системе и представляет энергию взаимодействия тел (поднятый над Землёй камень и земля – потенциальная энергия взаимодействия камня и Земли).
Изменение потенциальной энергии ∆Еп также определяется работой, совершаемой силами, действующими на материальную точку при её перемещении.
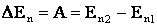
Данное уравнение не дает полного определения величины потенциальной энергии в каждой точке, а определяет лишь изменение потенциальной энергии при переходе от точки к точке. Абсолютная величина Еп зависит от выбора начала отсчета потенциальной энергии (где потенциальная энергия равна нулю).
Выбор уровня с нулевой энергии произволен (или бесконечность, или поверхность Земли и т.д.).
Если работа силы по любой замкнутой траектории равна нулю, то такие силы называют консервативными или потенциальными. К ним относятся силы тяжести, упругости, электростатического взаимодействия. Вид выражения для потенциальной энергии зависит от вида действующей силы:
|
|
а) для силы тяжести:
Еп = mgh,
где h – высота над поверхностью Земли (или выбранного нулевого уровня).
б) для силы упругости:
,
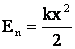где x – смещение от нулевого положения – точки, где x = 0.
Сумма кинетической Ek и потенциальной En энергий тела называют полной механической энергией E:
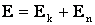
Для замкнутой системы материальных тел выполняются закон сохранения механической энергии – при любых процессах, происходящих в системе тел, её полная механическая энергия остается постоянной:
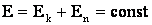
Если система незамкнутая, то изменение полной механической энергии (её уменьшение) равно работе внешних сил (например, работе против сил сопротивления):
.
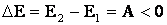В механизмах и машинах нельзя получить больше работы, чем затрачено энергии. К тому же часть энергии теряется (на преодоление силы трения, обращается в тепло), поэтому полезная работа An машины всегда меньше затраченной работы Аз (An < Аз). Величина, показывающая какую долю составляет полезная работа от всей совершенной (затраченной), называется коэффициентом полезного действия (КПД).
КПД(ŋ) равен выраженному в процентах отношению полезной работы к затраченной:
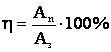
КПД также можно выразить и через мощность:
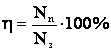
Ударом называется столкновение двух или более тел, при котором взаимодействие длится очень короткое время.
Центральным ударом называется удар, при котором тела до удара движутся вдоль прямой, проходящий через их центры масс.
Абсолютно упругий удар – это удар, в результате которого в обоих взаимодействующих телах не остаётся никаких деформаций и тела после взаимодействия движутся раздельно.
Для случая прямого центрального абсолютно упругого удара выполняются:
а) закон сохранения импульса:
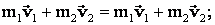
б) закон сохранения кинетической энергии:
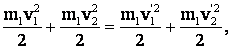
где v2 и v1 – скорости тела до удара,
v΄2 и v΄1 – скорости после удара.
Столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело, называются абсолютно неупругим ударом.
Для случая прямого центрального абсолютного удара применимы:
а) закон сохранения импульса:
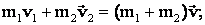
б) закон сохранения кинетической энергии с учетом “потери” энергии Е потерь на деформацию:
,
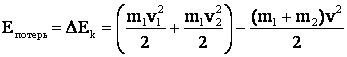где v2 и v1– скорости тела до удара,
v– скорость единого тела после соударения.
Задача №1. Оконная штора массы 1 кг и длины 2 м свертывается в тонкий валик над окном. Какая при этом совершается работа? Трением пренебречь.
| m = 1 кг; ℓ = 2 м; g = 9,8 м/с2. |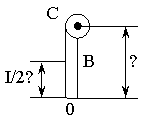 
|
| А –? | |
Решение: при свертывании шторы происходит увеличение ее потенциальной энергии. В начальный момент эта энергия W1:
,
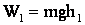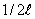где h1 – положение центра тяжести развернутой шторы, который находится в геометрическом центре шторы и отстоит от точки О на величину I/2ℓ, следовательно:
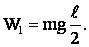
В конечном положении центр тяжести свернутой шторы находится на высоте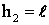 
, потенциальная энергия:
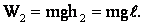
По закону, сохранения энергии:
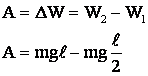
Проверка единиц измерения:
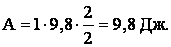
Ответ: работа по свертыванию шторы равна 9,8 Дж.
Задача №2. Какую работу необходимо произвести, чтобы телеграфный столб массой 200 кг, к вершине которого прикреплена крестовина массой 30 кг, перевести из горизонтального положения в вертикальное? Длина столба 10 м.
| m1 = 200 кг; m2 = 30 кг; ℓ = 10 м; g = 9,8 м/с2. |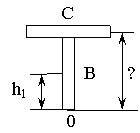 
|
| А –? |
Решение: примем начальную энергию системы столб – перекладина, когда они находятся на земле, за нуль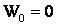 
.
В конечном положении полная энергия, системы будет складываться из потенциальной энергии столба и перекладины:
,
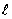
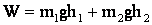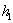где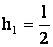 
– положение центра тяжести столба;
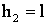– положение центра тяжести перекладины.
Следовательно: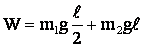 
.
По закону сохранения энергии:
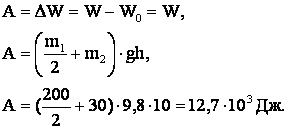
Ответ. 12,7·103 Дж.
Задача №3. Пуля перед ударом о земляную насыпь имела скорость 400 м/с и углубилась на расстояние 0,5 м. Определить силу сопротивления насыпи движению пули, если масса ее 24 г.
| m = 24·10-3 кг; ℓ = 0,5 м; v = 400 м/с. |
| Fc –? |
Решение: к моменту удара о насыпь пуля обладала кинетической энергией:
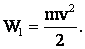
Углубившись на расстояние ℓ пуля остановилась, и ее энергия обратилась в нуль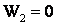 
.
Это изменение энергии произошло за счет работы против силы сопротивления:
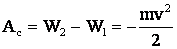
С другой стороны: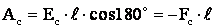 
Откуда 
Проверка единиц измерения:
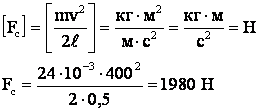
Ответ: 1980 H.
Задача №4. Мотор самолета массой mвыключается во время горизонтального полета со скоростью v1на высоте h. Самолет планирующий полетом достигает земли со скоростью v2, меньшей, чем v1. Определить среднюю силу сопротивления воздуха при спуске самолета, принимая длину спуска равной ℓ.
| m; v1; v2; h; ℓ; g. |
| Fc –? |
Решение: в начальный момент движения полная энергия самолета складывалась из кинетической и потенциальной:
(1)
К моменту приземления потенциальная энергия самолета уменьшилась до нуля, полная энергия в этот момент стала равной только кинетической:
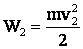(2)
Изменение полной энергии тела произошло за счет работы внешних сил, в нашем случае за счет силы сопротивления. По закону сохранения энергии с учетом работы внесших сил получим:
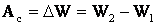(3)
По определению работы:
,
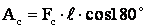где Fc– величина силы сопротивления,
α = 180° – угол между направлением силы и направлением перемещения.
Вектор Fc всегда направлен в сторону, противоположную движению.
Итак: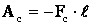 
(4)
Подставляя (1), (2), (4) в (3), получим:
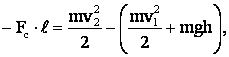
откуда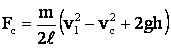 
Задача №5. Какой кинетической энергией обладало тело массой 2 кг, если оно поднялось по наклонной плоскости с углом наклона 30° на высоту 1 м? Коэффициент трения между телом и наклонной плоскостью 0,1.
| m = 2 кг; α = 30°; h = 1 м; k = 0,1; g = 9,8 м/с2. | 
|
| К1 –? |
Решение: в начальный момент тело обладало кинетической энергией К1. В конечный момент – потенциальной: П2 = mgh.
По закону сохранения энергии работа силы трения:
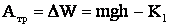
с другой стороны: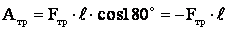 
,
где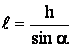 
итак: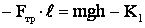 
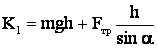(1)
Силу трения скольжения определим через коэффициент трения:
,
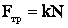где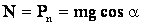 
.
Следовательно: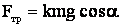 
, (2)
подставляя (2) в (1), получим:
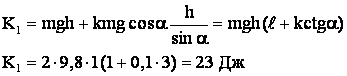
Ответ: кинетическая энергия тела в начале подъема была 23 Дж.
Задача №6. Поезд движется на подъем со скоростью 36 км/ч. Определить мощность, развиваемую локомотива, если сила тяги локомотива рана 300 кН.
| v = 36км/ч = 10м/с; Fт = 300 кН = 3·105 Н. |
| N –? |
Решение: по определению, мощность:
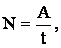
где А – работа силы тяги:
,
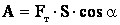т.к. нашем случае угол α = 0, то
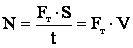
Размерность искомой величины:
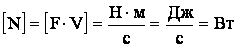
N = 3·105·10 = 3·106 Вт = 3 МВт.
Ответ: мощность локомотива на подъеме 3 MBт.
Задача №7. Два неупругих шара массами 2.кг и 3 кг движутся со скоростями соответственно 8 м/с и 4 м/с. Определить увеличение внутренней энергии шаров при их столкновении, если меньший шар нагоняет больший. Удар считать не упругим.
| m1 = 2 кг; m2 = 3 кг; v1 =8 м/с; v2= 4 м/с. |
| ΔW –? |
Решение: запишем закон сохранения импульса для неупругого удара шаров:
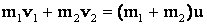
Определим скорость uшаров после взаимодействия
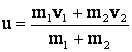(1)
По закону сохранения энергии изменение внутренней энергия шаров будет иметь вид
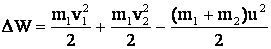(2)
Решив совместно уравнения (I) и (2), будем иметь:
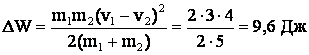
Ответ: Внутренняя энергия шаров увеличится на 9,6 Дж.
Задача №8. Тела с массами 2 кг и 3 кг двигаются навстречу друг другу со скоростями 2 м/с и 1 м/с. Найти скорость тел после абсолютно упругого столкновения. Трением пренебречь.
| m1 = 2 кг; m2 = 3 кг; v1 =2 м/с; v2= 1 м/с. | 
|
| u1, u2 –? |
Решение: схема столкновения изображена на рисунке. При абсолютно упругом ударе двух тел выполняется закон сохранения импульса:
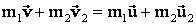
который в проекциях на ось Охимеет вид:
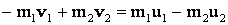(1)
Выполняется также закон сохранения механической энергии, которая в данном случае совпадает с кинетической энергией тел:
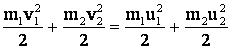(2)
Решаем совместно систему уравнений (1)-(2), которая при подстановке числовых данных имеет вид:
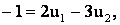(3)
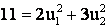(4)
Выражаем из (3) скорость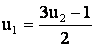 
и подставляем в (4), тогда получаем квадратное уравнение для определения U2:
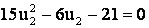
Решение уравнения (5) имеет вид:
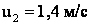
тогда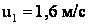 
Заметим, если сценарий столкновения выбирается отличным от изображенного на рис., то ответы будут те же, но с точностью до знаков. При этом в окончательных выражениях знаки минус надо опустить.
Ответ: скорость тел после столкновения равна u1 = 1,6 м/с, u2 = 1,4 м/с.
Задача №9. В шар массой 1,5 кг, подвешенный на тонком стержне длиной 0,7 м, попадает и застревает в нем пуля массой 10 г, летевшая наклонно сверху вниз под утлом 30° к горизонту со скоростью 500 м/с. На какой угол γ откачнется шар с пулей?
| m = 1,5 кг; m1 = 10-2 кг; ℓ = 0,7 м; α = 30°; v= 500 м/с. |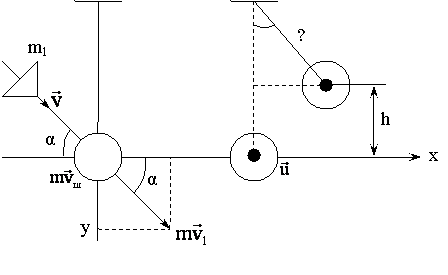 
|
| γ –? |
Решение: в горизонтальном направлении на пулю и шар внешние силы не действуют, поэтому сумма проекций импульсов пули и шара на ось Ox не меняется:
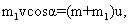
где u – скорость шара сразу после попадания пули.
Отсюда: 
При максимальном отклонении, согласно закону сохранения энергии, имеем:
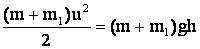
Из последнего уравнения находим h:
.
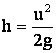Как видно из рисунка: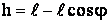 
.
Тогда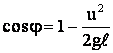 
,
или окончательно имеем:
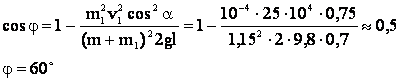
Ответ: угол отклонения составляет 60°.
Задача №10. Человек стоит на покоящейся тележке и бросает горизонтально камень массой 8 кг со скоростью 5 м/с. Определить, какую работу совершит при этой человек, если масса тележки вместе с человеком 160 кг?
| m = 8 кг; М = 160 кг; v = 5 м/с. |
| A –? |
Решение: камень и тележка после взаимодействия приобретают кинетическую энергию. Следовательно, работа человека по закону сохранения энергия, равна сумме кинетических энергий камня и тележки:
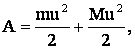
где u – скорость тележки после броска камня.
Эту скорость найдем по закону сохранения импульса:
,
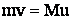откуда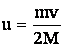 
.
Следовательно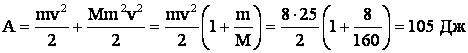 
Ответ: человек совершит работу равную 105 Дж.
Задача №11. Ящик с песком массой 15 кг удерживается пружиной, жесткость которой 30 Н/см. Пуля массой 10 г, движущаяся со скоростью 600 м/с, попадает в ящик и застревает в ней. Определить на сколько при этом сожмется пружина.
| m = 10 г = 10-2кг; М = 15 кг; K = 30 Н/см= 3·103 Н/м; v = 600 м/с. |
| ∆х –? |
Решение: пуля, взаимодействуя с ящиком, сообщает ему скорость u, которую найден по закону сохранения импульса:
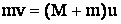
или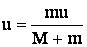 
По закону сохранения энергии кинетическая энергия ящика:
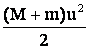
равна потенциальной энергии сжатой пружины:
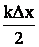
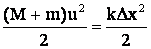
Откуда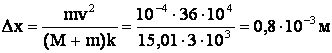 
Ответ: пружина сжимается на 0,8 мм.
Задача №12. Молот массой 5 кг ударяет небольшой кусок железа, лежащий на наковальне. Масса наковальни 100 кг. Массой куска железа пренебречь. Удар неупругий. Определить, к.п.д. удара молота?
| m = 50кг; М = 100 кг. |
| ŋ –? |
Решение: энергию, идущую на деформацию куска железа, следует считать полезной:
W = W1 – W2,
где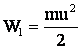 
– энергия молота в момент удара о наковальню;
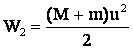– энергия наковальни непосредственно после удара.
Скорость u наковальни после удара определим по закону сохранения импульс:
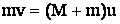
КПД удара молота равен отношению энергии W, затраченной на деформацию куска железа, ко всей затраченной энергии W1:
,
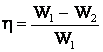или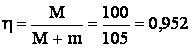 
Ответ: КПД удара ŋ = 95,2%.
Задача №13. Верхний конец стального стержня закреплен неподвижно, к нижнему подвешен груз массой 2000 кг. Начальная длина стержня5 м, сечение 4 см2. Определить абсолютное и относительное удлинение стержня и напряжение материала стержня. Модуль Юнга для стали 2,2·1011Па.
| S = 4 см2 = 4·10-4 м2; M = 2·103 кг; ℓ0 = 5 м; E = 2,2·1011 Па. | 
|
| Δℓ, ε, σ –? |
Решение: деформация стержня происходит под действием силы тяжести подвешенного к стержню груза F = mg. По определению напряжения:
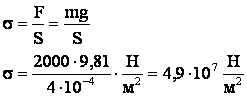
Относительное удлинение найдем из закона Гука:
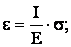
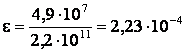
По определению относительного удлинения:
,
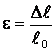откуда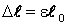 
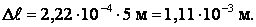
Ответ: ∆ℓ = 1,11·10-3 м = 1,11 мм, ε = 2,23·10-4, σ = 4,9·107 Н/м2.
Задача №14. Определить работу растяжения двух соединенных последовательно пружин жесткостями k1 = 400 H/м и k2 = 250 Н/м, если первая пружина при этом растянулась на ∆ℓ1 = 2 см.
| k1 = 400 H/м; k2 = 250 Н/м; ∆ℓ =2 см = 2·10-2 м. |
| A –? |
Решение: внешняя сила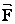 
одинакова по величине для пружин 1 и 2. Тогда, согласно закону Гука:
;
.
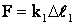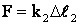Найдем растяжение второй пружины:
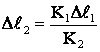(1)
Общая работа А по растяжению пружин равна сумме работ по растяжению каждой пружины:
A = A1+A2 (2)
Учитывая, что работа внешней силы идет на сообщение пружине потенциальной энергии, получим:
;
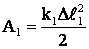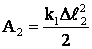(3)
Решим совместно уравнения (1), (2), (3):
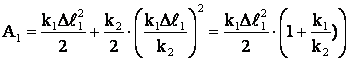
Проверка единиц измерения:
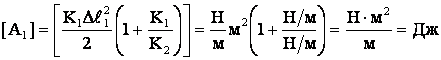
Ответ: работа растяжения пружины равна 0,208 Дж.
Задача №15. Определить КПД установки водоснабжения, если бак водоизмещением 40 м3, размещенный на высоте 10 м, наполняется водой за 12 мин насосом мощностью 7 кВт.
| V = 40 м3; t= 12 мин = 720 сек; N = 7 кВт = 7·103 Вт; ρ = 103 кг/м3; g = 9,8 м/с2. |
| η –? |
Решение: КПД определяется по формуле:
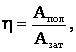
где Апол – полезная работа, в данном случав это работа по наполнению бака водой;
Азат – затраченная работа, работа произведенная насосом.
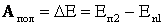, (1)
где En1 = 0, En2 = mgh – потенциальная энергия поднятой воды:
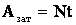(2)
Тогда ŋ с учетом уравнений (1) и (2):
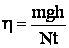
Зная, что плотность равна:
,
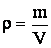имеем: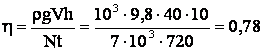 
Проверка единиц измерения:
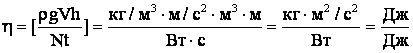
Ответ: КПД установки 78%.