Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава III, § 2, п. 34), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
Мы продолжаем знакомство с многогранниками.
На прошлом занятии вы познакомились с частным видом пирамиды –правильной пирамидой.
Напомню, что пирамида называется правильной, если в её основании лежит правильный многоугольник. Высотой такой пирамиды называется отрезок, проведённый из вершины в центр основания.
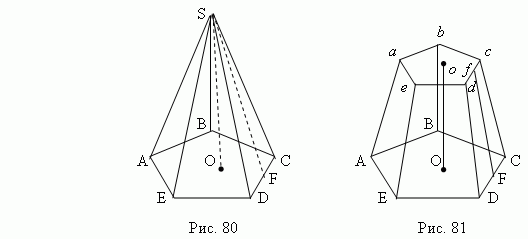
Изобразим произвольную пирамиду SA1 A2… An.
Проведём секущую плоскость параллельно основанию, пересекающую боковые рёбра пирамиды в точках В1 В2… Вn.
Секущая плоскость разбила пирамиду на два многогранника, один из которых так же является пирамидой., а другой называется усечённой пирамидой.
Часть пирамиды, между основанием и сечением, параллельным основанию пирамиды, назовём усечённой пирамидой.
Усечённая пирамида имеет два основания -
параллельные, подобные многоугольники.
Отрезки, соединяющие вершины оснований называются боковыми рёбрами усечённой пирамиды.
На чертеже изображена усечённая пирамида ABCDA1 B1 C1 D1.
Высотой пирамиды называется перпендикуляр, проведённый из любой точки основания к плоскости другого.
ABCDA1 B1 C1 D1-усечённая пирамида, ABCD и A1 B1 C1 D1 –основания, А А1В1 В - боковая грань,
А А1-боковое ребро, ОО1-высота, B1E – высота боковой грани.
Очевидно, что все боковые грани усечённой пирамиды являются трапециями.
Если усечённая пирамида получена путём сечения параллельно основанию правильной пирамиды, то усеченная пирамида будет так же правильной.
Основания правильной усечённой пирамиды –это правильные многоугольники, а боковые грани- равнобедренные трапеции.
Высота боковой грани называется апофемой.
Сумма площадей боковых граней называется площадью боковой поверхности усечённой пирамиды. Для правильной усечённой пирамиды площадь боковой поверхности равна произведению апофемы на полусумму периметров оснований.
Задача 1. В пирамиде проведено сечение параллельно основанию через середину высоты. Площадь основания равна Q. Найти площадь сечения.
Решение: так как сечение проходит через середины боковых ребер, то каждая сторона многоугольника (сечения) является средней линей боковой грани и равна половине стороны многоугольника, находящегося в основании. То есть можно сказать, что основание и сечение, подобные многоугольники, к=2. А площади подобных фигур относятся квадрат коэффициента подобия. Значит, площадь сечения равна Q/4.
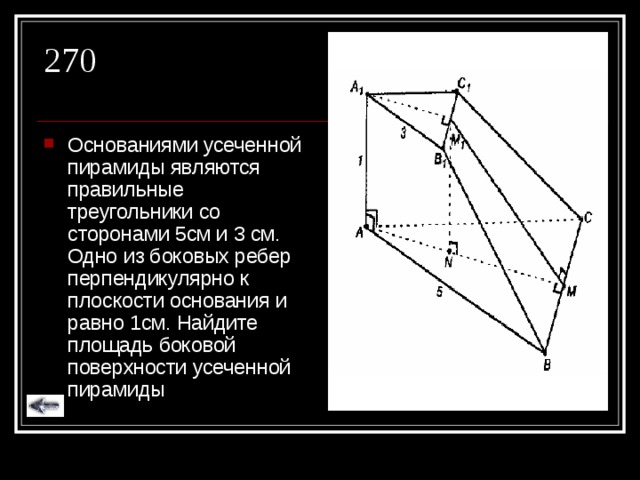Задача 2. Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 см и 3 см. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности усеченной пирамиды.
Решение: две грани усеченной пирамиды будут являться прямоугольными трапециями и будут равны между собой, их площадь равна 
см2. Третья грань является равнобедренной трапецией, найдем высоту этой грани, а затем и площадь. Боковое ребро пирамиды равно 
см, высота боковой грани равна 
см, площадь боковой грани равна 
см2. Таким образом, площадь боковой поверхности усеченной пирамиды равна 16 см2.
Задача 3.
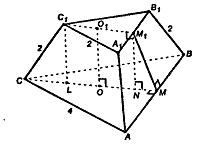Стороны оснований правильной треугольной усечённой пирамиды равны 4 дм и 2 дм. Точки О и О1-центры оснований пирамиды. Найти высоту и апофему пирамиды, если боковое ребро равно 2 дм.
Для начала проведём краткий анализ задачи: так как усечённая пирамида правильная, то боковые рёбра-равные равнобедренные трапеции. В основании лежат правильные треугольники, значит все углы этих треугольников будут по 60 градусов.
Решение:
1. Дополнительное построение: построим СМ перпендикулярно АВ, С1М1 перпендикулярно А1В1 и соединим точки М1 и М.
По теореме о трёх перпендикулярах М1М перпендикулярен АВ(одновременно М1М перпендикулярна А1В1), значит М1М-апофема.
2. Поскольку точки О и О1-центры оснований пирамиды, то ОО1-высота h.
Дополнительное построение: построим С1L перпендикулярно СМ и М1 N так же перпендикулярно СМ.
Тогда С1L= ОО1= М1 N=h(как расстояния между параллельными прямыми).
3.Треугольники АВС и А1 В1 С1-правильные, значит ОС и О1С1-радиусы описанных окружностей треугольников АВС и А1 В1 С1.
Найдем ОС и О1С1по формуле для нахождения радиуса описанной окружности 
дм. 
дм.
4. Найдем длину отрезка СL как разность между длинами отрезков ОС и О1С1: 
дм.
5. Из прямоугольного треугольника СС1L найдём
С1 L по теореме Пифагора: 
Так как С1L= ОО1=h, следовательно высота h равна 
6. Т. к. C1O1 в 2 раза больше O1M1, то O1M1=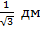 
.
Аналогично OM= 
дм.
7. Рассмотрим прямоугольный треугольник M1NM и найдем длину отрезка M1М по теореме Пифагора: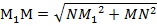 
; MN= ОМ – ОN. ON= O1M1= 
. 
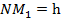
Ответ: 
, О1О= 
дм
Самостоятельная работа
1. Определить высоту правильной усечённой четырёхугольной пирамиды, если даны боковое ребро с и стороны а и b нижнего и верхнего оснований.
2. В правильной четырёхугольной усечённой пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Определить боковое ребро этой усечённой пирамиды.
Контрольные вопросы:
1. Какой многогранник называется усечённой пирамидой?
2. Сколько оснований имеет усечённая пирамида?
3. Формула для вычисления площади боковой поверхности правильной усечённой пирамиды?