1°. Собственные и присоединенные векторы линейного преобразования.
Пусть 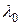 – некоторое собственное значение преобразования
– некоторое собственное значение преобразования 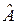 , т. е. справедливо следующее определение.
, т. е. справедливо следующее определение.
Определение 1. Вектор 
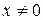 называется собственным вектором преобразования
называется собственным вектором преобразования 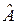 , отвечающим собственному значению
, отвечающим собственному значению 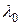 , если
, если
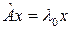 , т.е. , т.е. 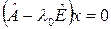 . .
| (1) |
Рассмотрим совокупность всех векторов, удовлетворяющих условию (1) при фиксированном 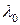 .Ясно, что совокупность этих векторов является подпространством пространства
.Ясно, что совокупность этих векторов является подпространством пространства 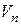 .
.
Мы обозначим его 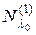 . Легко видеть, что
. Легко видеть, что 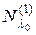 инвариантно относительно преобразования
инвариантно относительно преобразования 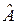 (проверьте!).
(проверьте!).
Заметим, что подпространство 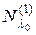 состоит из всех собственных векторов преобразования
состоит из всех собственных векторов преобразования 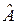 , отвечающих собственному значению
, отвечающих собственному значению 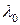 , к которым добавлен еще нулевой вектор.
, к которым добавлен еще нулевой вектор.
Определение 2. Вектор 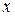 называется присоединенным вектором первого порядка преобразования
называется присоединенным вектором первого порядка преобразования 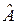 , отвечающим собственному значению
, отвечающим собственному значению 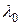 , если вектор
, если вектор 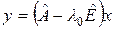 является собственным вектором преобразования
является собственным вектором преобразования  .
.
Пусть 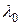 – собственное значение преобразования
– собственное значение преобразования 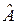 . Рассмотрим подпространство, состоящее из всех векторов
. Рассмотрим подпространство, состоящее из всех векторов 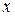 , для которых выполнено условие
, для которых выполнено условие
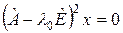 , ,
| (2) |
т.е. ядро преобразования 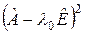 Обозначим это подпространство
Обозначим это подпространство 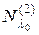 . Очевидно, что
. Очевидно, что 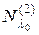 является инвариантным подпространством пространства
является инвариантным подпространством пространства 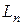 . В самом деле, пусть
. В самом деле, пусть 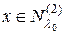 , т.е.
, т.е. 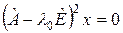 . Нам надо доказать, что и вектор
. Нам надо доказать, что и вектор 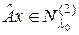 , т.е. что
, т.е. что 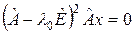 . Это следует из того, что преобразование
. Это следует из того, что преобразование 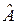 перестановочно с
перестановочно с 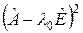 , т.е.
, т.е. 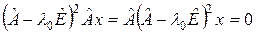 .
.
Рассмотрим несколько более подробно структуру пространства 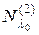 . В нем есть векторы двух типов.
. В нем есть векторы двух типов.
Если 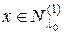 , т.е.
, т.е. 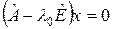 , то тогда и
, то тогда и 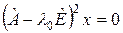 , т.е.
, т.е. 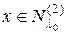 . Таким образом,
. Таким образом, 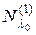 целиком содержится в
целиком содержится в 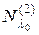 . Если
. Если 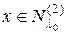 , но
, но 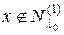 , т.е.
, т.е. 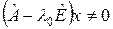 ,
, 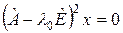 , то
, то 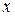 – присоединенный вектор первого порядка. Действительно, в этом случае
– присоединенный вектор первого порядка. Действительно, в этом случае 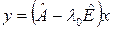 есть собственный вектор.
есть собственный вектор.
Таким образом, подпространство 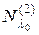 получается, если к подпространству
получается, если к подпространству 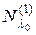 добавить присоединенные векторы первого порядка.
добавить присоединенные векторы первого порядка.
|
|
Аналогично вводим подпространство 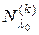 , состоящее из всех векторов
, состоящее из всех векторов 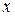 , для которых
, для которых
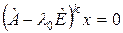 . .
| (3) |
Это подпространство инвариантно относительно преобразования 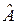 . Ясно, что подпространство
. Ясно, что подпространство 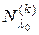 содержит предыдущее подпространство
содержит предыдущее подпространство 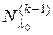 .
.
Определение 3. Вектор 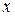 называется присоединенным вектором
называется присоединенным вектором 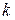 –го порядка, если вектор
–го порядка, если вектор 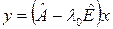 является присоединенным вектором
является присоединенным вектором 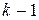 – го порядка.
– го порядка.
По индукции можно показать, что если 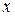 – присоединенный вектор
– присоединенный вектор 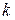 – го порядка, то
– го порядка, то 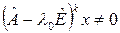 ,
, 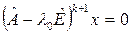 . Другими словами, присоединенным вектором
. Другими словами, присоединенным вектором 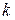 –го порядка называется вектор, принадлежащий
–го порядка называется вектор, принадлежащий 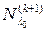 и не принадлежащий
и не принадлежащий 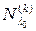 .
.
Пример. Пусть 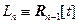 пространство многочленов степени
пространство многочленов степени 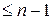 и преобразование
и преобразование  – дифференцирование:
– дифференцирование: 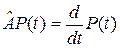 . Легко видеть, что
. Легко видеть, что 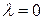 есть собственное значение. Соответствующий ему собственный вектор
есть собственное значение. Соответствующий ему собственный вектор 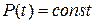 . Найдем для этого преобразования пространства
. Найдем для этого преобразования пространства 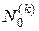 . По определению
. По определению 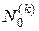 состоит из всех многочленов
состоит из всех многочленов 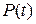 , для которых
, для которых 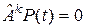 , т.е.
, т.е. 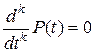 . Это будут все многочлены, степень которых не превышает
. Это будут все многочлены, степень которых не превышает 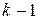 . Присоединенными векторами
. Присоединенными векторами 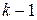 -го порядка будут многочлены, степень которых в точности равна
-го порядка будут многочлены, степень которых в точности равна 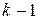 .
.
В этом примере размерность каждого из подпространств 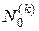 равна
равна 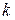 и она растет от
и она растет от 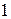 до
до 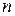 вместе с ростом
вместе с ростом 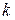 . Подпространство
. Подпространство 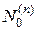 уже совпадает со всем пространством
уже совпадает со всем пространством 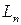 , и если мы захотим определить
, и если мы захотим определить 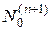 ,
, 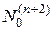 и т.д., то все эти подпространства будут совпадать с
и т.д., то все эти подпространства будут совпадать с 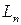 .
.
Легко видеть также, что в этом примере 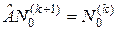 . Это следует из того, что каждый многочлен степени
. Это следует из того, что каждый многочлен степени 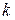 есть производная от многочлена степени
есть производная от многочлена степени 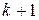 .
.
Упражнение. Показать, что для любого линейного преобразования 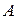 имеет место включение
имеет место включение 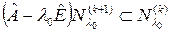 .
.
Пусть  – линейное преобразование, а
– линейное преобразование, а 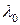 – его собственное значение. Покажем, что подпространства
– его собственное значение. Покажем, что подпространства 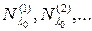 сначала строго возрастают с ростом индекса, а затем, начиная с некоторого номера
сначала строго возрастают с ростом индекса, а затем, начиная с некоторого номера 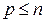 , этот рост прекращается, т.е.
, этот рост прекращается, т.е. 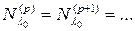 (смотрите приведенный в этом пункте пример).
(смотрите приведенный в этом пункте пример).
|
|
Мы уже показали, что каждое подпространство 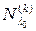 содержит
содержит 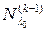 , т.е. что с увеличением номера подпространства
, т.е. что с увеличением номера подпространства 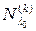 , а значит и из размерности, могут только увеличиваться.
, а значит и из размерности, могут только увеличиваться.
Так как наше пространство конечномерно, то для какого–то 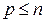 мы впервые получим, что
мы впервые получим, что 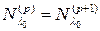 .
.
Докажем, что в этом случае 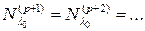 , т.е. что дальнейшего возрастания подпространства не будет.
, т.е. что дальнейшего возрастания подпространства не будет.
Действительно, предположим противное, а именно, что 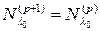 , но для некоторого
, но для некоторого 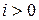 подпространство
подпространство 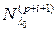 строго больше, чем
строго больше, чем 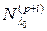 . Тогда существует вектор
. Тогда существует вектор 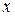 такой, что
такой, что 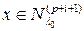 ,
,  . Это значит, что
. Это значит, что
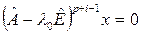 , но , но 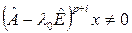 . .
| (4) |
Обозначим через 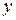 вектор
вектор 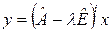 . Тогда первое из выражений (4) означает, что
. Тогда первое из выражений (4) означает, что 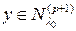 , а второе, что
, а второе, что 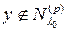 , что невозможно, так как подпространства
, что невозможно, так как подпространства 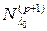 и
и 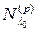 по предположению совпадают.
по предположению совпадают.
Итак, пусть 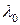 – некоторое собственное значение преобразования
– некоторое собственное значение преобразования  . Основным результатом этого пункта является построение инвариантного подпространства
. Основным результатом этого пункта является построение инвариантного подпространства 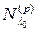 , состоящего из всех собственных и присоединенных векторов, отвечающих этому собственному значению. Его называют корневым подпространством, соответствующим собственному числу
, состоящего из всех собственных и присоединенных векторов, отвечающих этому собственному значению. Его называют корневым подпространством, соответствующим собственному числу 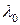 . Кроме того, в п. 3 нам понадобится более детальная структура
. Кроме того, в п. 3 нам понадобится более детальная структура 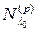 . А именно, обозначая через
. А именно, обозначая через 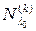 подпространство, состоящее из присоединенных векторов порядка
подпространство, состоящее из присоединенных векторов порядка 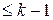 , мы получили возрастающую цепочку инвариантных подпространств
, мы получили возрастающую цепочку инвариантных подпространств
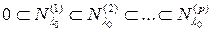 . .
| (5) |
Все члены этой цепочки различны. Подпространство 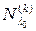 состоит при этом из всех векторов
состоит при этом из всех векторов 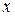 , для которых
, для которых 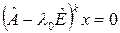 , т.е. это есть ядро преобразования
, т.е. это есть ядро преобразования 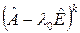 .
.
|
|
Преобразование 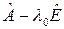 переводит каждое из подпространств цепочки (5) в предшествующее.
переводит каждое из подпространств цепочки (5) в предшествующее.
2о. Прямая сумма подпространств
Пусть  и
и 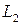 – два подпространства линейного пространства
– два подпространства линейного пространства 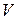 .
.
Определение 4. Будем говорить, что векторное пространство 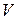 представляет собой прямую сумму подпространств
представляет собой прямую сумму подпространств 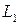 и
и 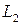 , если
, если 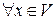 может быть единственным образом представлен в виде суммы
может быть единственным образом представлен в виде суммы 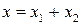 , где
, где 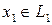 ,
, 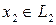 .
.
Обозначение. 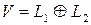 .
.
В этом случае говорят, что 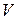 разложимо в прямую сумму подпространств.
разложимо в прямую сумму подпространств.
Обобщение. Если 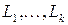 – подпространства
– подпространства 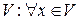 мжет быть единственным образом представлен в виде
мжет быть единственным образом представлен в виде 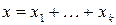 , где
, где 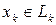 , то сумма
, то сумма 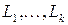 называется прямой суммой и обозначается
называется прямой суммой и обозначается 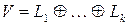 .
.
Пример. Пусть 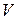 –
– 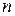 –мерное линейное пространство с базисом
–мерное линейное пространство с базисом 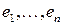 . Пусть
. Пусть 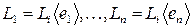 , т.е.
, т.е. 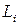 – линейная оболочка, натянутая на вектор
– линейная оболочка, натянутая на вектор 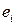 :.Тогда
:.Тогда 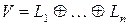 .
.
Возможность других представлений следует из
Теорема 1. Для того, чтобы пространство 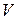 было прямой суммой своих подпространст
было прямой суммой своих подпространст 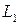 и
и 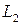 достаточно, чтобы
достаточно, чтобы 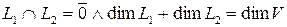 .
.
Доказательство. Пусть  – базис
– базис 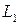 и
и 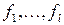 – базис в
– базис в 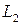 и
и 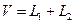 . Докажем, что
. Докажем, что 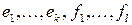 – базис в
– базис в 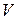 . Так как по условию
. Так как по условию 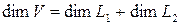 , то достаточно показать, что
, то достаточно показать, что 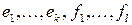 – линейно независимы. Рассмотрим линейную комбинацию этих элементов и приравняем её к нулю:
– линейно независимы. Рассмотрим линейную комбинацию этих элементов и приравняем её к нулю:
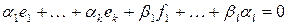
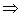
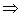
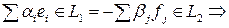
т.к. слева  , а справа
, а справа 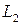 , а
, а 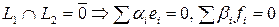
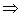
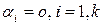 ,
, 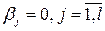
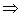 вектора
вектора 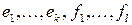 – линейно независимы.
– линейно независимы.
Таким образом, 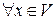 может быть разложен по базису:
может быть разложен по базису:
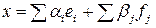 ,
,
где 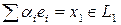 и
и 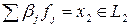 , т.е.
, т.е. 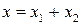 .
.
Осталось показать, что такое представление единственно. 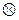
Пусть 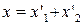 и
и 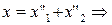
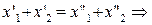
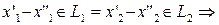 т.к.
т.к. 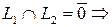
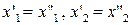 . ■
. ■
Замечание. Если 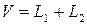 , но сумма не прямая, то представление
, но сумма не прямая, то представление 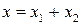 не единственно. Например,
не единственно. Например,
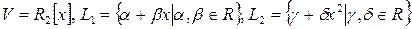
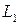 и
и 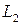 – подпространства и
– подпространства и 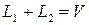 . На
. На 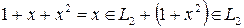 и
и 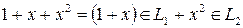 . Иначе дело обстоит, если
. Иначе дело обстоит, если 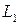 – такое же, а
– такое же, а 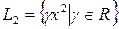 .
.
3°. Выделение подпространства, в котором преобразование  имеет только одно собственное значение.
имеет только одно собственное значение.
Пусть 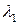 – некоторое собственное значение преобразования
– некоторое собственное значение преобразования  . В этом пункте мы покажем, что пространство
. В этом пункте мы покажем, что пространство 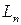 можно разложить в прямую сумму двух инвариантных подпространств, в первом из которых преобразование
можно разложить в прямую сумму двух инвариантных подпространств, в первом из которых преобразование  имеет лишь одно собственное значение
имеет лишь одно собственное значение 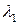 , а во втором у преобразования
, а во втором у преобразования  уже нет собственного значения
уже нет собственного значения 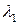 .
.
Не ограничивая общности, можно считать, что 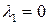 .
.
Действительно, пусть 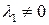 . Рассмотрим преобразование
. Рассмотрим преобразование 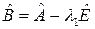 . Оно уже имеет собственное значение, равное нулю[1]. Очевидно, что инвариантные подпространства преобразований
. Оно уже имеет собственное значение, равное нулю[1]. Очевидно, что инвариантные подпространства преобразований  и
и 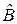 совпадают.
совпадают.
Итак, впредь мы считать, что преобразование имеет собственное значение 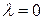 . Рассмотрим введенное в п. 1 инвариантное подпространство
. Рассмотрим введенное в п. 1 инвариантное подпространство 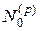 , состоящее из всех собственных и присоединенных векторов преобразования
, состоящее из всех собственных и присоединенных векторов преобразования  , отвечающих собственному значению
, отвечающих собственному значению 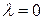 . Как мы помним, оно является ядром преобразования
. Как мы помним, оно является ядром преобразования 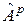 , т.е. состоит их всех векторов
, т.е. состоит их всех векторов 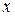 , для которых
, для которых 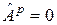 .
.
В качестве второго слагаемого прямой суммы мы возьмем подпространство 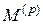 – образ пространства
– образ пространства 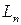 при том же преобразовании
при том же преобразовании 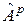 .
.
Легко видеть, что 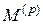 также инвариантно относительно преобразования
также инвариантно относительно преобразования  . Действительно, если
. Действительно, если 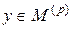 , т.е.
, т.е. 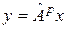 , то
, то  , т.е.
, т.е.  также принадлежит
также принадлежит 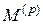 .
.
Теорема 2. Пространство 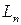 можно разложить в прямую сумму инвариантных подпространств
можно разложить в прямую сумму инвариантных подпространств 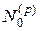 и
и 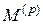 . При этом подпространство
. При этом подпространство 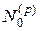 состоит только из собственных и присоединенных векторов, отвечающих собственному значению
состоит только из собственных и присоединенных векторов, отвечающих собственному значению 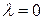 , а в подпространстве
, а в подпространстве 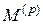 преобразование
преобразование  обратимо (т.е.
обратимо (т.е. 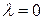 не является собственным значением преобразования
не является собственным значением преобразования  в подпространстве
в подпространстве 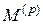 ).
).
Доказательство. Для доказательства первого утверждения нам достаточно показать, что пересечение подпространств 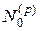 и
и 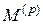 равно нулю. Допустим противное, т.е. пусть существует такой вектор
равно нулю. Допустим противное, т.е. пусть существует такой вектор 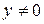 такой, что
такой, что 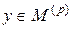 и
и 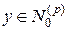 . Так как
. Так как 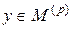 , то
, то
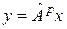 . .
| (6) |
Далее, так как 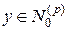 , то
, то
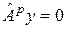 . .
| (7) |
Но из (6) и (7) следует, что существует такой вектор 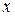 , для которого
, для которого 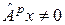 и в то же время
и в то же время  . Это значит, что
. Это значит, что 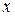 есть присоединенный вектор преобразования
есть присоединенный вектор преобразования  с собственным значением
с собственным значением 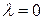 , не принадлежащий подпространству
, не принадлежащий подпространству 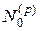 , что невозможно, так как
, что невозможно, так как 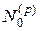 состоит из всех таких векторов.
состоит из всех таких векторов.
Таким образом, мы доказали, что пересечение 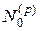 и
и 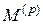 равно нулю. Так как сумма размерностей этих подпространств равна
равно нулю. Так как сумма размерностей этих подпространств равна 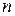 (это ядро и образ преобразования
(это ядро и образ преобразования 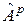 ), то отсюда следует, что пространство
), то отсюда следует, что пространство 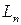 раскладывается в прямую сумму этих подпространств:
раскладывается в прямую сумму этих подпространств:
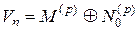 . .
| (8) |
Докажем теперь второе утверждение теоремы, т.е. что в подпространстве 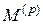 преобразование
преобразование  не имеет нулевого собственного значения. Действительно, если бы это было так, то в
не имеет нулевого собственного значения. Действительно, если бы это было так, то в 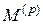 существовал бы вектор
существовал бы вектор 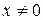 такой, что
такой, что 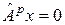 . Но это равенство означает, что
. Но это равенство означает, что 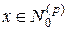 , т.е. является общим вектором
, т.е. является общим вектором 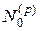 и
и 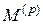 , а мы доказали, что таким вектором может быть только нуль. ■
, а мы доказали, что таким вектором может быть только нуль. ■
Теперь мы можем освободиться от предположения, что выделенное подпространство отвечает нулевому собственному значению, и считать установленным следующий факт.
Если 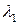 – некоторое собственное значение преобразования
– некоторое собственное значение преобразования  , то пространство
, то пространство 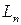 можно разложить в прямую сумму инвариантных подпространств
можно разложить в прямую сумму инвариантных подпространств 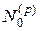 и
и 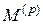 , в первом из которых преобразование
, в первом из которых преобразование  имеет только собственное значение
имеет только собственное значение 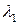 , а во втором все собственные значения
, а во втором все собственные значения  отличны от
отличны от 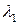 .
.
Применяя полученный результат к преобразованию  в пространстве
в пространстве 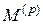 и к некоторому собственному значению
и к некоторому собственному значению 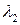 этого преобразования, мы «отщепим» инвариантное подпространство, отвечающее собственному значению
этого преобразования, мы «отщепим» инвариантное подпространство, отвечающее собственному значению 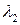 . Продолжая этот процесс, пока не будут исчерпаны все собственные значения преобразования
. Продолжая этот процесс, пока не будут исчерпаны все собственные значения преобразования  , мы получим доказательство следующей теоремы:
, мы получим доказательство следующей теоремы:
Теорема 3. Пусть преобразование  пространства
пространства 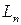 имеет
имеет 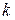 различных собственных значений
различных собственных значений  . Тогда
. Тогда 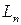 можно разложить в прямую сумму
можно разложить в прямую сумму 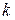 инвариантных подпространств
инвариантных подпространств 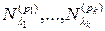 :
:
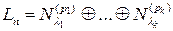 . .
| (9) |
Каждое из подпространств 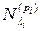 состоит только из собственных и присоединенных векторов, отвечающих собственному значению
состоит только из собственных и присоединенных векторов, отвечающих собственному значению 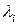 .
.
Другими словами, для каждого 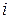 существует такое число
существует такое число 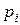 , что для всех
, что для всех 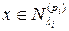 выполнено
выполнено 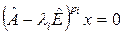 .
.
У нас осталась еще одна, впрочем, не менее важна задача – выбрать в каждом подпространстве базис, в котором матрица преобразования имеет жорданову нормальную форму. Это будет сделано в следующем пункте.
3°. Приведение к нормальной форме матрицы с одним собственным значением.
В случае если пространство состоит только из собственных векторов, базис в пространстве можно выбирать произвольно и матрица преобразования в этом базисе имеет диагональный вид.
В общем случае, чтобы выбрать базис, в котором матрица преобразования имеет наиболее простой вид, мы будем строить цепочки собственных и присоединенных векторов, выбрав некоторый базис в подпространстве 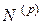 и последовательно применяя к векторам этого базиса преобразование
и последовательно применяя к векторам этого базиса преобразование  .
.
Определение 5. Векторы из пространства 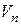 называются линейно независимыми относительно подпространства
называются линейно независимыми относительно подпространства 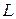 , если их линейная комбинация, отличная от нуля, не принадлежит
, если их линейная комбинация, отличная от нуля, не принадлежит 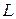 .
.
Заметим, что всякие линейно зависимые векторы из 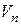 линейно зависимы относительно любого подпространства.
линейно зависимы относительно любого подпространства.
Определение 5. Базисом пространства 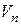 относительно подпространства
относительно подпространства 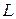 называется такая система
называется такая система  линейно независимых векторов из
линейно независимых векторов из 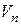 , которая после пополнения каким-нибудь базисом из
, которая после пополнения каким-нибудь базисом из 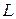 образует базис во всем пространстве.
образует базис во всем пространстве.
Такой базис легко построить. Для этого достаточно выбрать какой-нибудь базис в 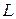 , дополнить его до базиса во всём пространстве и затем отбросить векторы исходного базиса из
, дополнить его до базиса во всём пространстве и затем отбросить векторы исходного базиса из  . Число векторов в таком относительном базисе равно разности размерностей пространства и подпространства.
. Число векторов в таком относительном базисе равно разности размерностей пространства и подпространства.
Всякую систему линейно независимых векторов относительно 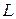 можно дополнить до базиса относительно
можно дополнить до базиса относительно 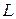 . Для этого нужно к выбранным векторам добавить какой–нибудь базис подпространства
. Для этого нужно к выбранным векторам добавить какой–нибудь базис подпространства 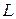 . Получится некоторая система векторов из
. Получится некоторая система векторов из 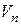 , которые, как легко проверить, линейно независимы. Чтобы получить базис относительно
, которые, как легко проверить, линейно независимы. Чтобы получить базис относительно 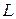 , нужно дополнить эту систему до базиса во всем пространстве
, нужно дополнить эту систему до базиса во всем пространстве 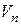 , а затем отбросить базис подпространства
, а затем отбросить базис подпространства 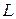 .
.
Итак, пусть преобразование 
 в пространстве
в пространстве 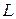 имеет только одно собственное значение. Не ограничивая общности, можно предположить, что оно равно нулю.
имеет только одно собственное значение. Не ограничивая общности, можно предположить, что оно равно нулю.
Рассмотрим снова цепочку (5) подпространств, полученных в п.1:
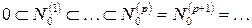 ,
,
где подпространство 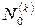 есть ядро преобразования
есть ядро преобразования 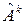 . Так как преобразование
. Так как преобразование  в пространстве
в пространстве 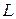 не имеет отличных то нуля собственных значений, то, очевидно,
не имеет отличных то нуля собственных значений, то, очевидно, 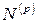 совпадает при этом со всем пространством
совпадает при этом со всем пространством 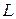 .
.
Выберем в максимальном из этих подпространств 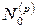 базис относительно содержащегося в нем подпространства
базис относительно содержащегося в нем подпространства 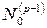 . Пусть векторы этого базиса будут
. Пусть векторы этого базиса будут
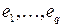 . .
| (10) |
Очевидно, что это будут присоединенные векторы 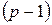 –го порядка. Мы уже видели (см. упражнение на стр.211), что
–го порядка. Мы уже видели (см. упражнение на стр.211), что 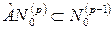 . Поэтому векторы
. Поэтому векторы
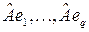
лежат в 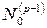 . Покажем, что эти векторы линейно независимы в
. Покажем, что эти векторы линейно независимы в 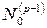 относительно лежащего в нем подпространства
относительно лежащего в нем подпространства  .
. 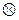 Действительно, пусть не все
Действительно, пусть не все 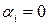 и
и
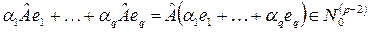 . .
| (11) |
Тогда вектор 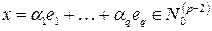 , а это противоречит предположению, что векторы
, а это противоречит предположению, что векторы 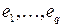 линейно независимы над
линейно независимы над 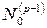 .
.
Дополним векторы 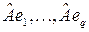 до базиса в
до базиса в 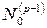 относительно
относительно  . Мы получим тогда
. Мы получим тогда 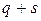 векторов
векторов 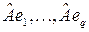 ,
, 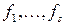 , которые представляют собой максимальное число линейно независимых присоединенных векторов порядка
, которые представляют собой максимальное число линейно независимых присоединенных векторов порядка 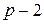 .
.
Снова применим к этим векторам преобразование  и полученную систему векторов из
и полученную систему векторов из  дополним, как и выше, до базиса в
дополним, как и выше, до базиса в  относительно
относительно 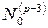 . Продолжая этот процесс, мы дойдем до подпространства
. Продолжая этот процесс, мы дойдем до подпространства 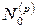 и выберем базис в этом пространстве, состоящий из максимального числа линейно независимых собственных векторов.
и выберем базис в этом пространстве, состоящий из максимального числа линейно независимых собственных векторов.
Расположим полученные векторы в следующую таблицу
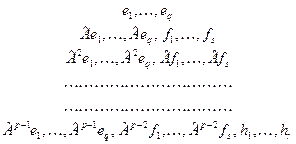 . .
| (12) |
Векторы нижней строчки образуют базис в подпространстве 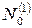 . Векторы двух нижних строчек образуют базис в
. Векторы двух нижних строчек образуют базис в 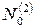 , так как это есть базис
, так как это есть базис 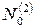 относительно
относительно 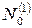 в соединении с базисом
в соединении с базисом 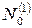 . Векторы трех нижних строчек образуют базис в
. Векторы трех нижних строчек образуют базис в 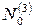 и т.д. Наконец, все векторы таблицы образуют базис в
и т.д. Наконец, все векторы таблицы образуют базис в 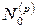 , т.е. во всем пространстве
, т.е. во всем пространстве 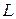 .
.
Покажем, что в этом базисе матрица преобразования  имеет жорданову нормальную форму. Действительно, рассмотрим произвольный столбец таблицы (12), например, для определенности первый.
имеет жорданову нормальную форму. Действительно, рассмотрим произвольный столбец таблицы (12), например, для определенности первый.
Обозначим для удобства 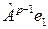 через
через 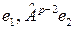 – через
– через 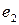 и т.д. и рассмотрим действие преобразования
и т.д. и рассмотрим действие преобразования  на каждый из этих векторов. Так как
на каждый из этих векторов. Так как 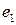 – собственный вектор, отвечающий нулевому собственному значению, то
– собственный вектор, отвечающий нулевому собственному значению, то 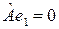 .
.
Дальше, по определению,
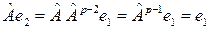
и аналогично
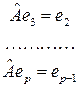 .
.
Таким образом, преобразование  переводит векторы первого столбца снова в себя, т.е. подпространство
переводит векторы первого столбца снова в себя, т.е. подпространство 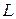 , натянутое на эти векторы, инвариантно относительно
, натянутое на эти векторы, инвариантно относительно  . Матрица преобразования
. Матрица преобразования 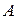 в подпространстве
в подпространстве 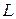 в базисе
в базисе 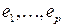 имеет вид
имеет вид
 . .
| (13) |
Матрица (13) есть жорданова клетка, отвечающая собственному значению 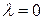 . Обозначается
. Обозначается 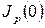 . Аналогичное инвариантное подпространство отвечает каждому из столбцов таблицы (12), и размерность каждого такого подпространства равна числу векторов в соответствующем столбце. Так как матрица преобразования
. Аналогичное инвариантное подпространство отвечает каждому из столбцов таблицы (12), и размерность каждого такого подпространства равна числу векторов в соответствующем столбце. Так как матрица преобразования 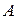 в базисе, состоящем из векторов какого-либо столбца таблицы (12), имеет вид (13), то матрица преобразования во всем пространстве
в базисе, состоящем из векторов какого-либо столбца таблицы (12), имеет вид (13), то матрица преобразования во всем пространстве 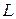 в базисе, состоящем из всех векторов таблицы (12), состоит из жордановых клеток, число которых равно числу столбцов в этой таблице, а размер каждой клетки равен числу векторов соответствующего столбца.
в базисе, состоящем из всех векторов таблицы (12), состоит из жордановых клеток, число которых равно числу столбцов в этой таблице, а размер каждой клетки равен числу векторов соответствующего столбца.
Если вместо преобразования  рассмотреть преобразование
рассмотреть преобразование 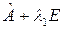 , то, так как матрица преобразования
, то, так как матрица преобразования 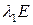 диагональна, мы получим тот же результат для преобразования пространства
диагональна, мы получим тот же результат для преобразования пространства 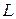 , имеющего только одно собственное значение, равное произвольному числу
, имеющего только одно собственное значение, равное произвольному числу 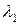 . Соответствующие жордановы клетки матрицы преобразования
. Соответствующие жордановы клетки матрицы преобразования 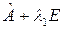 будут иметь вид:
будут иметь вид:
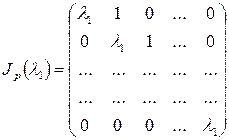 . .
| (14) |
Вспоминая теперь, что для произвольного преобразования  мы можем разложить пространство
мы можем разложить пространство 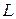 в сумму инвариантных подпространств, в каждом из которых преобразование
в сумму инвариантных подпространств, в каждом из которых преобразование  имеет только одно собственное значение (см. формулу (11)), мы получаем отсюда полное доказательство теоремы.
имеет только одно собственное значение (см. формулу (11)), мы получаем отсюда полное доказательство теоремы.
Теорема 4. Пусть задано произвольное линейное преобразование  в комплексном пространстве
в комплексном пространстве 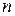 измерений. Предположим, что у
измерений. Предположим, что у  имеется
имеется 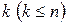 линейно независимых собственных векторов
линейно независимых собственных векторов
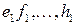 ,
,
соответствующих собственным значениям 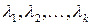 . Тогда существует базис, состоящий из
. Тогда существует базис, состоящий из 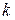 групп векторов *):
групп векторов *):
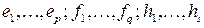 , ,
| (1) |
В котором преобразование  имеет следующий вид:
имеет следующий вид:
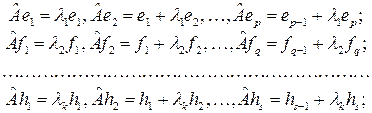 , ,
| (2) |
5o. Примеры.
Найти жорданову форму матрицы и матрицу перехода к жордановому базису для преобразования, заданного в исходном базисе матрицей
а) 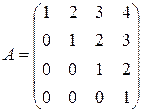 .
.
Характеристический многочлен 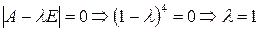 – собственное значение.
– собственное значение. 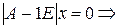
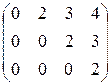 ~
~ 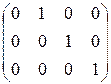
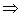 единственный собственный вектор
единственный собственный вектор 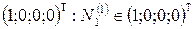 .
.
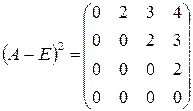
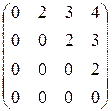 =
= 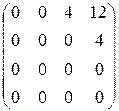 .
.