Линейное преобразование, сопряженное данному
1º. Определения, свойства.
Здесь изучаются линейные преобразования в евклидовых пространствах, т.е. в линейных пространствах со скалярным произведением.
Определение 1. Линейное преобразование 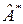 евклидово пространство называется сопряженным данному преобразованию
евклидово пространство называется сопряженным данному преобразованию 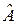 , если
, если  E
E 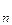 :
:
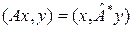 (1)
(1)
Лемма 1. а) Если произведение данной строки на произвольный столбец равно нулю, то строка равна нулю;
б) Если произведение произвольной строки на данный столбец равно нулю, то столбец состоит из нулей.
Доказательство:
а) Рассмотрим строку 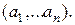 Ее произведением на столбец
Ее произведением на столбец 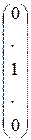 –
– 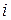 –ая строка равно
–ая строка равно 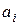 и равно 0
и равно 0 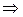
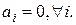
б) Аналогично. ■
Пусть E 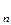 –
– 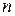 –мерное евклидово пространство и пусть для симметричного преобразования
–мерное евклидово пространство и пусть для симметричного преобразования 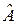
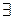 сопряженное ему преобразование
сопряженное ему преобразование 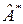 .
.
Пусть 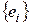 – базис в E
– базис в E 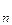 . Выясним, как связаны матрицы
. Выясним, как связаны матрицы 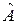 и
и 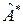 . Пусть в базисе
. Пусть в базисе 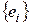 они имеют матрицы
они имеют матрицы 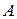 и
и 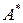 . Тогда (1) примет вид:
. Тогда (1) примет вид:
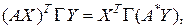
где 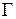 – матрица Грама базиса
– матрица Грама базиса 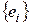 . Тогда
. Тогда
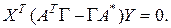
в силу леммы 1 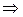
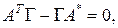 (2)
(2)
где 0 – нулевая матрица.
Если базис 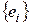 – ортонормированный, то
– ортонормированный, то 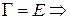
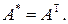 (3)
(3)
Утверждение 1. Каждое линейное преобразование в евклидовом пространстве имеет сопряженное преобразование, причем единственное.
Доказательство:
В E 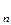 выберем ортонормированный базис
выберем ортонормированный базис 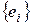 . Пусть
. Пусть 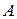 – матрица линейного преобразования
– матрица линейного преобразования 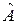 и пусть
и пусть 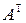 – матрица некоторого преобразования
– матрица некоторого преобразования 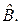 Тогда условие (1) с преобразованием
Тогда условие (1) с преобразованием 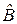 приводит к следующему:
приводит к следующему:
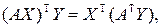
т.е. 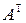 – матрица сопряженного преобразования. Если бы было два преобразования, сопряженных
– матрица сопряженного преобразования. Если бы было два преобразования, сопряженных 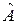 , то в силу (3) их бы матрицы совпадали. ■
, то в силу (3) их бы матрицы совпадали. ■
Свойства сопряженных операторов.
1°. 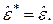
2°. 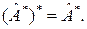 Следует из того, что
Следует из того, что 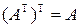 и утверждения 1.
и утверждения 1.
3°. 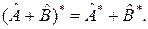
4°. 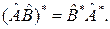
5°. 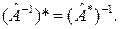
Доказательство: самостоятельно.
Утверждение 2. Если подпространство 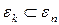 инвариантно относительно
инвариантно относительно 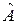 , ортогональное к нему дополнение
, ортогональное к нему дополнение 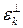 инвариантно относительно
инвариантно относительно 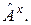
Доказательство:
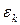 инвариантно относительно
инвариантно относительно 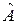
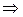
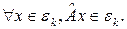
Пусть 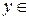
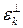

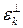 . ■
. ■
Утверждение 3. Характеристический многочлен сопряженного преобразования совпадает с характеристическим многочленом самого линейного преобразования.
Доказательство:
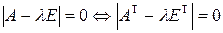 , т.к.
, т.к. 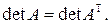
2º. Самосопряженные преобразования.
Определение 2. Линейное преобразование 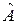 евклидова пространства называется самосопряженным или симметрическим, если
евклидова пространства называется самосопряженным или симметрическим, если 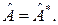
Утверждение 4. Преобразование является самосопряженным 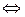 его матрица в любом ортонормированном базисе симметрическая (т.е. удовлетворяет условию
его матрица в любом ортонормированном базисе симметрическая (т.е. удовлетворяет условию 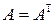 ).
).
Теорема 1. Характеристические числа самосопряженного линейного оператора вещественны.
Доказательство:
Пусть 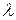 – собственное значение самосопряженного линейного оператора
– собственное значение самосопряженного линейного оператора 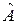 , т.е.
, т.е. 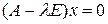 . Для вещественной матрицы
. Для вещественной матрицы 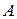
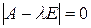 имеет наряду с
имеет наряду с 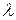 корень
корень 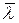 . Покажем, что
. Покажем, что 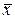 – соответствующий собственный вектор. Действительно,
– соответствующий собственный вектор. Действительно, 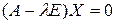
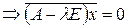
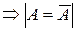
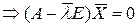 . Покажем далее, что
. Покажем далее, что 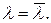
Имеем 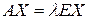

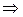 выполняя транспонирование
выполняя транспонирование
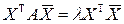 (*)
(*)
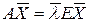
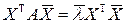
 (**)
(**)
Вычитая (*)–(**), имеем: 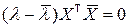 . Т.к.
. Т.к. 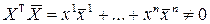 – вещественное число
– вещественное число 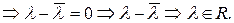 ■
■
Следствие. Если 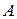 – симметричная матрица, то все корни уравнения
– симметричная матрица, то все корни уравнения 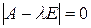 – вещественные.
– вещественные.
Теорема 2. Собственные векторы самосопряженного преобразования 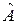 , принадлежащие различным собственным значениям, ортогональны.
, принадлежащие различным собственным значениям, ортогональны.
Доказательство:
Пусть 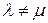 и
и 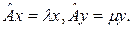 Тогда
Тогда 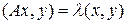 и
и 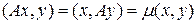
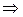
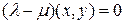
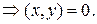 ■
■
Теорема 3. Если 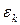 – инвариантное подпространство относительно самосопряженного преобразования
– инвариантное подпространство относительно самосопряженного преобразования 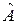 , то его ортогональное дополнение
, то его ортогональное дополнение 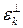 – тоже инвариантное подпространство.
– тоже инвариантное подпространство.
Доказательство:
Пусть 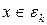 , т.е.
, т.е. 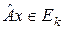 . Пусть
. Пусть 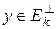 , т.е.
, т.е. 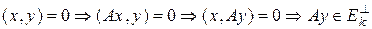 . ■
. ■
Теорема 4. Пусть 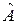 – самосопряженное линейное преобразование в
– самосопряженное линейное преобразование в 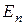 . Тогда в
. Тогда в 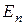 существует ортонормированный базис из собственных векторов.
существует ортонормированный базис из собственных векторов.
Доказательство:
Методом математической индукции по числу измерений 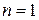 . Очевидно, т.к.
. Очевидно, т.к. 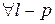 – собственный для
– собственный для 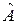
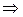 искомый базис – вектор длины 1.
искомый базис – вектор длины 1.
Пусть для 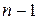 верно. Докажем для
верно. Докажем для 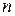 . По теореме 1
. По теореме 1 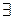 хотя бы одно собственное значение
хотя бы одно собственное значение 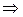
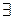 хотя бы одно одномерное инвариантное подпространство
хотя бы одно одномерное инвариантное подпространство 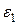 . Пусть
. Пусть 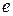 – единичный вектор в нем. По теореме 3 ортогональное дополнение
– единичный вектор в нем. По теореме 3 ортогональное дополнение 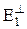 – инвариантное подпространство размерности
– инвариантное подпространство размерности 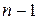 .
.
Пусть 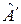 – сужение
– сужение 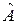 на
на 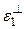 (
(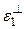 =
= 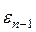 ). Тогда
). Тогда 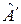 – самосопряженный на
– самосопряженный на 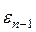 , т.к.
, т.к.  выполнено для
выполнено для 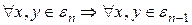
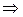
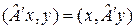 . Более того, если
. Более того, если 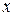 – собственный вектор для
– собственный вектор для 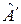 , то он собственный для
, то он собственный для 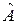 .
.
По предположению индукции в 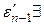
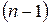 – мерный ортонормированный базис из собственных векторов для
– мерный ортонормированный базис из собственных векторов для 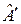
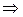
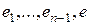 – ортонормированный базис из E
– ортонормированный базис из E 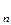 (
(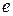
 вектору
вектору 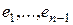 , а они ортогональны по предположению индукции). ■
, а они ортогональны по предположению индукции). ■
Следствие. Если 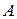 – симметрическая матрица, то
– симметрическая матрица, то 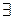 ортогональная матрица
ортогональная матрица 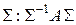 – диагональная матрица.
– диагональная матрица.
Доказательство:
Следует из того, что в базисе собственных векторов матрица принимает диагональный вид. ■
Для построения такого базиса находят собственные вектора. Если собственные вектора принадлежат разным собственным значениям, то по теореме 2 они ортогональны, если 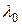 – кратный корень, то полученные собственные вектора нужно ортогонализовать и нормировать.
– кратный корень, то полученные собственные вектора нужно ортогонализовать и нормировать.