| Приставка | Множитель | |
| Наименование | Обозначение | |
| экса | Э | 1018 |
| пэта | П | 1015 |
| тера | Т | 1012 |
| гига | Г | 109 |
| мега | М | 106 |
| Кило | К | 103 |
| Гекто | Г | 102 |
| Дека | Да | 101 |
| Деци | Д | 10-1 |
| Санти | С | 10-2 |
| Милли | М | 10-3 |
| Микро | Мк | 10-6 |
| Нано | Н | 10-9 |
| Пико | П | 10-12 |
| Фемто | Ф | 10-15 |
| Атто | А | 10-18 |
- Греческий алфавит
| Обозначения букв | Названия букв |
| A, a | Альфа |
| B, b | Бета |
| G, g | Гамма |
| D, d | Дэльта |
| E, e | Эпсилон |
| Z, V | Дзета |
| H, h | Эта |
| Q, J | Тэта |
| I, i | Иота |
| K, æ | Каппа |
| L, l | Лямбда |
| M, m | Мю |
| N, n | Ню |
| X, x | Кси |
| O, o | Омикрон |
| P, p | Пи |
| R, r | Ро |
| S, s | Сигма |
| T, t | Тау |
- 59 -
| Воздух | 1,29 |
| Гелий | 0,18 |
| Кислород | 1,43 |
- Коэффициент поверхностного натяжения.
| Жидкость | Коэффициент, мН/м |
| Вода | |
| Мыльная пена | |
| Ртуть | |
| Спирт |
- Эффективный диаметр молекулы
| Газ | Диаметр, м |
| Азот | 3,0×10-10 |
| Водород | 2,3×10-10 |
| Гелий | 1,9×10-10 |
| Кислород | 2,7×10-10 |
- Относительные атомные массы (округленные значения) Ar и порядковые номера Z некоторых элементов.
| Элемент | Символ | Ar | Z |
| Азот | N | ||
| Алюминий | Al | ||
| Аргон | Ar | ||
| Барий | Ba | ||
| Ванадий | V | ||
| Водород | H | ||
| Вольфрам | W | ||
| Гелий | He | ||
| Железо | Fe | ||
| Золото | Au | ||
| Калий | K | ||
| Кальций | Ca | ||
| Кислород | O | ||
| Магний | Mg | ||
| Марганец | Mn | ||
| Медь | Cu | ||
| Молибден | Mo | ||
| Натрий | Na | ||
| Неон | Ne | ||
| Никель | Ni | ||
| Олово | Sn | ||
| Платина | Pt | ||
| Ртуть | Hg | ||
| Сера | S | ||
| Серебро | Ag | ||
| Углерод | C | ||
| Уран | U | ||
| Хлор | Cl |
– 6 –
Модуль углового ускорения

Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
 , at = eR, an = w2 R,
, at = eR, an = w2 R,
где  – модуль линейной скорости; at и аn – модули тангенциального и нормального ускорений; w – модуль угловой скорости; e – модуль углового ускорения; R – радиус окружности.
– модуль линейной скорости; at и аn – модули тангенциального и нормального ускорений; w – модуль угловой скорости; e – модуль углового ускорения; R – радиус окружности.
Модуль полного ускорения
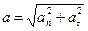 , или а = R
, или а = R  .
.
Угол между полным а и нормальным аn ускорениями

Кинематическое уравнение гармонических колебаний материальной точки
х = A cos(wt + j),
где х – смещение, А – амплитуда колебаний, w – угловая или циклическая частота, j – начальная фаза. Скорость и ускорение материальной точки, совершающей гармонические колебания:
 ; а = – Aw2 соs(wt + j).
; а = – Aw2 соs(wt + j).
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания
 ;
;
б) начальная фаза результирующего колебания

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,
х = А1 соswt; у= A2 соs(wt+j):
a) у=  , если разность фаз j=0;
, если разность фаз j=0;
– 7 –
б) у= 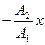 , если разность фаз j=±p;
, если разность фаз j=±p;
в)  =1, если разность фаз j=±p/2
=1, если разность фаз j=±p/2
Уравнение плоской бегущей волны
y = A cosw(t-x/  )
)
где у — смещение любой из точек среды с координатой х в момент t,  — скорость распространения колебаний в среде.
— скорость распространения колебаний в среде.
Связь разности фаз Dj колебаний с расстоянием Dх между точками среды, отсчитанным в направлении распространения колебаний:
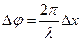
где λ – длина волны.
Импульс материальной точки массой m, движущейся со скоростью  ,
,
p =m 
Второй закон Ньютона
dp = F dt,
где F – результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости
F = – kx,
где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;
б) сила тяжести
P = mg;
в) сила гравитационного взаимодействия
 ,
,
где G – гравитационная постоянная, m1 и m2 – массы взаимодействующих тел, r –расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через
– 58 –
ПРИЛОЖЕНИЯ
- Основные физические постоянные (округленные значения).
| Физическая постоянная | Обозначение | Значение |
| Нормальное ускорение свободного падения | G | 9,81м/c2 |
| Гравитационная постоянная | Γ | 6,67×10-11м3/(кг×с2) |
| Постоянная Авогадро | NA | 6,02×1023 моль-1 |
| Универсальная газовая постоянная | R | 8,31 Дж/(моль×К) |
| Молярный объем идеального газа при нормальных условиях (стандартный объем) | Vm | 22,4×10-3 м3/моль |
| Постоянная Больцмана | K | 1,38×10-23Дж/K |
- Некоторые астрономические величины
| Наименование | Значения |
| Радиус Земли | 6,37×106 м |
| Масса Земли | 5,98×1024 кг |
| Радиус Солнца | 6,95×108 м |
| Масса Солнца | 1,98×1030 кг |
| Радиус Луны | 1,74×106 м |
| Масса Луны | 7,33×1022 кг |
| Расстояние от центра Земли до Центра Солнца | 1,49×1011 м |
| Расстояние от центра Земли до центра Луны | 3,84×108 м |
- Плотность твердых тел, жидкостей и газов (при нормальных условиях).
| Вещество | Плотность, кг/м3 |
| Алюминий | 2,70×103 |
| Барий | 3,50×103 |
| Ванадий | 6,02×103 |
| Висмут | 9,80×103 |
| Железо | 7,88×103 |
| Литий | 0,53×103 |
| Медь | 8,93×103 |
| Никель | 8,90×103 |
| Свинец | 11,3×103 |
| Серебро | 10,5×103 |
| Цезий | 1,90×103 |
| Цинк | 7,15×103 |
| Вода (при 40С) | 1,00×103 |
| Глицерин | 1,26×103 |
| Ртуть | 13,6×103 |
| Сероуглерод | 1,26×103 |
| Спирт | 0,80×103 |
| Водород | 0,09 |
– 57 –
d=0,8мм, опущенную в воду на малую глубину. Считать смачивание полным.
272. Какую работу А надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от V1=8см3 до V2=16см3? Считать процесс изотермическим.
273. Какая энергия Е выделится при слиянии двух капель ртути диаметром d1=0,8мм и d2=1,2мм в одну каплю?
274. Определить давление р внутри воздушного пузырька диаметром d=4мм, находящегося в воде у самой ее поверхности. Считать атмосферное давление нормальным. Пространство между двумя стеклянными параллельными пластинками с площадью поверхности S=100см2 каждая, расположенными на расстоянии l = 20 мкм друг от друга, заполнено водой. Определить силу F, прижимающую пластинки друг к другу. Считать мениск вогнутым с диаметром d, равным расстоянию между пластинками.
275. Глицерин поднялся в капиллярной трубке диаметром канала d=1 мм на высоту h=20мм. Определить поверхностное натяжение a глицерина. Считать смачивание полным.
276. В воду опущена на очень малую глубину стеклянная трубка с диаметром канала d=1мм. Определить массу т воды, вошедшей в трубку.
277. На сколько давление р воздуха внутри мыльного пузыря больше нормального атмосферного давления ро, если диаметр пузыря d=5мм?
278. Воздушный пузырек диаметром d=2,2 мкм находится в воде у самой ее поверхности. Определить плотность r воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.
279. Две капли ртути радиусом r=1,2мм каждая слились в одну большую каплю. Определить энергию Е, которая выделится при этом слиянии. Считать процесс изотермическим.
– 8 –
напряженность 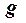 гравитационного поля:
гравитационного поля:
F = m g
г) сила трения скольжения
F=fN,
где f – коэффициент трения, N – сила нормального давления.
Закон сохранения импульса
 ,
,
или для двух тел (i=2)
m1  1+m2
1+m2  2= m1 u 1 + m2 u2 ,
2= m1 u 1 + m2 u2 ,
где  и
и  – скорости тел в момент времени, принятый за начальный;
– скорости тел в момент времени, принятый за начальный;
u1 и u2 – скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно,
 , или
, или 
Потенциальная энергия:
а) упругодеформированной пружины
П= ½ kx2
где k – жесткость пружины, х –абсолютная деформация;
б) гравитационного взаимодействия
 ,
,
где G – гравитационная постоянная, m1 и m2 – массы взаимодействующих тел, r –расстояние между ними (тела рассматриваются как материальные точки),
в) тела, находящегося в однородном поле силы тяжести,
П = mgh
где g — ускорение свободного падения; h — высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R –радиус Земли).
Закон сохранения механической энергии в поле консервативных сил
E=Т+П=const.
– 9 –
Работа А, совершаемая результирующей силой над материальной точкой:
А= F∙∆r∙cosα
и равна изменению кинетической энергии материальной точки:
A=DT=T2 - T1
Основное уравнение динамики вращательного движения относительно неподвижной оси z
Мz =Jze,
где Мz – результирующий момент внешних сил относительно оси z, действующих на тело, e – угловое ускорение, Jz – момент инерции относительно оси вращения.
Моменты инерции некоторых тел массой т относительно оси z, проходящей через центр масс:
а) стержня длиной l относительно оси, перпендикулярной стержню:

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра):
Jz=mR2,
где R – радиус обруча (цилиндра);
в) диска (сплошного цилиндра) радиусом R относительно оси, перпендикулярной плоскости диска:
Jz= ½ mR2.
Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z:
Lz=Jzw,
где w – угловая скорость тела.
Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z:
Jzw=const,
где Jz – момент инерции системы тел относительно оси z, w – угловая скорость вращения тел системы вокруг оси z.
– 56 –
262. Идеальный газ совершает цикл Карно. Температура Т1 теплоотдатчика в четыре раза (n = 4) больше температуры теплоприемника. Какую долю w количества теплоты, полученного за один цикл от теплоотдатчика, газ отдаст теплоприемнику?
263. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, КПД которого h=0,4, если работа изотермического расширения равна A1=8Дж.
264..Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q2=14кДж. Определить температуру Т1 теплоотдатчика, если при температуре теплоприемника T2=280К работа цикла A=6кДж.
265. Газ, являясь рабочим веществом в цикле Карно, получил от теплоотдатчика теплоту Q1=4,38кДж и совершил работу А=2,4 кДж. Определить
температуру теплоотдатчика, если температура теплоприемника T2 =273 К.
266. Газ, совершающий цикл Карно, отдал теплоприемнику 67% теплоты, полученной от теплоотдатчика. Определить температуру T2 теплоприемника, если температура теплоотдатчика Т1=430 К.
267. Во сколько раз увеличится коэффициент полезного действия h цикла Карно при повышении температуры теплоотдатчика от Т1=380К до Т2=560 К? Температура теплоприемника T2 = 280 К.
268. Идеальная тепловая машина работает по циклу Карно. Температура теплоотдатчика Т1 = 500 К, температура теплоприемника T2 = 250К. Определить термически КПД h цикла, а также работу А1 рабочего вещества при изотермическом расширении, если при изотермическом сжатии совершена работа A2=70Дж.
269. Газ, совершающий цикл Карно, получает теплоту Q1=84кДж. Определить работу А газа, если температура Т1 теплоотдатчика в три раза выше температуры T2 теплоприемника.
270. В цикле Карно газ получил от теплоотдатчика теплоту Q1=500Дж и совершил работу A=100Дж. Температура теплоотдатчика Т1=400К. Определить температуру Т2 теплоприемника.
271. Найти массу m воды, вошедшей в стеклянную трубку с диаметром канала
- 55 -
р2=0,5МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление р3 газа в конце процесса.
254. Кислород массой m=200г занимает объем V1=100л и находится под давлением р1=200кПа. При нагревании газ расширился при постоянном давлении до объема V2=300л, а затем его давление возросло до р3=500кПа при неизменном объеме. Найти изменение внутренней энергии DU газа, совершенную газом работу A и теплоту Q, переданную газу. Построить график процесса.
255. Объем водорода при изотермическом расширении при температуре T=З00К увеличился в п=3 раза. Определить работу А, совершенную газом, и теплоту Q, полученную при этом. Масса т водорода равна 200 г.
256. Азот массой m=0,1кг был изобарно нагрет от температуры T1=200К до температуры T2=400К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение DU внутренней энергии азота.
257. Во сколько раз увеличится объем водорода, содержащий количество вещества n=0,4моль при изотермическом расширении, если при этом газ получит количество теплоты Q=800Дж? Температура водорода T=300К.
258. Какая работа А совершается при изотермическом расширении водорода массой m=5г, взятого при температуре T=290К, если объем газа увеличивается в три раза?
259. Какая доля w1 количества теплоты Q, подводимого к идеальному двухатомному газу при изобарном процессе, расходуется на увеличение DU внутренней энергии газа и какая доля w2 — на работу А расширения? Рассмотреть три случая, если газ: 1) одноатомный; 2)двухатомный; 3) трехатомный.
260. Определить работу А, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q=21кДж. Найти также изменение DU внутренней энергии газа.
261. Идеальный газ совершает цикл Карно при температурах теплоприемника T2=290К и теплоотдатчика Т1=400К. Во сколько раз увеличится коэффициент полезного действия h цикла, если температура теплоотдатчика возрастет до Т1= 600 К?
– 10 –
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z:
Т = ½ Jzw2, или  .
.
Примеры решения задач
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct3, где A =2 м, В =1 м/с, С= –0.5 м/с3. Найти координату х, скорость  x и ускорение аx точки в момент времени t =2с.
x и ускорение аx точки в момент времени t =2с.
Решение. Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t:
х = (2+1×2 – 0.5  23) м = 0.
23) м = 0.
Мгновенная скорость относительно оси х есть первая производная от координаты по времени:
 .
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
 .
.
В момент времени t = 2с
 x = (1-3×0,5×22) м/с= – 5 м/с; ах = б(— 0,5)×2 м/с2= – 6 м/с2.
x = (1-3×0,5×22) м/с= – 5 м/с; ах = б(— 0,5)×2 м/с2= – 6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону j=А+Вt+Ct2, где А=10 рад, В =20 рад/с, С= – 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r =0,1 м от оси вращения, для момента времени t=4 с.
 Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения аt, направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории (рис. 1):
Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения аt, направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории (рис. 1):
а = at +an.
Так как векторы ат и аn взаимно перпендикулярны, то модуль ускорения
– 11 –
 . (1)
. (1)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами аt = er, аn = w2r,
где w – модуль угловой скорости тела; e – модуль его углового ускорения. Подставляя выражения at и ап в формулу (1), находим
 . (2)
. (2)
Угловую скорость w найдем, взяв первую производную угла поворота по времени:  .
.
В момент времени t=4c модуль угловой скорости
w=[20 + 2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
e=dw/dt = 2С = — 4 рад/с2.
Подставляя значения w, e и r в формулу (2), получаем
а = 0,1  м/с2= 1,65 м/с2.
м/с2= 1,65 м/с2.
 Пример 3. Ящик массой т1 = 20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a=30° к рельсам.
Пример 3. Ящик массой т1 = 20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a=30° к рельсам.
Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел.
Но эта система не замкнута, так как на нее действуют внешние силы: силы тяжести m1g и m2g и сила реакции N2 (рис. 2). Поэтому применить закон сохранения импульса к системе ящик – тележка нельзя. Но так как проекции указанных сил на направление оси х, совпадающей с направлением рельсов, равны
нулю, то проекцию импульса системы на это направление можно считать
– 54 –
242. Определить среднюю длину свободного пробега  молекулы азота в сосуде вместимостью V=5л. Масса газа m = 0,5 г.
молекулы азота в сосуде вместимостью V=5л. Масса газа m = 0,5 г.
243. Водород находится под давлением р=20мкПа и имеет температуру T=300К. Определить среднюю длину свободного пробега  молекулы такого газа.
молекулы такого газа.
244. При нормальных условиях длина свободного пробега  молекулы
молекулы
водорода равна 0,160 мкм. Определить диаметр d молекулы водорода.
245. Какова средняя арифметическая скорость  молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега
молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега  молекулы кислорода при этих условиях равна 100 нм?
молекулы кислорода при этих условиях равна 100 нм?
246. Кислород находится под давлением р=133нПа при температуре T=200К. Вычислить среднее число <z> столкновений молекулы кислорода при этих условиях за время t= 1 с.
247. При каком давлении р средняя длина свободного пробега  молекул азота равна 1м, если температура газа t=10°С?
молекул азота равна 1м, если температура газа t=10°С?
248. В сосуде вместимостью V=5л находится водород массой m=0,5 г. Определить среднюю длину свободного пробега  молекулы водорода в этом сосуде.
молекулы водорода в этом сосуде.
249. Средняя длина свободного пробега  молекулы водорода при некоторых условиях равна 2мм. Найти плотность r водорода при этих условиях.
молекулы водорода при некоторых условиях равна 2мм. Найти плотность r водорода при этих условиях.
250. В сферической колбе вместимостью V=3л, содержащей азот, создан вакуум с давлением р=80мкПа. Температура газа T=250К. Можно ли считать вакуум в колбе высоким? Примечание. Вакуум считается высоким, если длина свободного пробега молекул в нем много больше линейных размеров сосуда.
251Определить количество теплоты Q, которое надо сообщить кислороду объемом V=50л при его изохорном нагревании, чтобы давление газа повысилось на Dр=0,5МПа.
251. При изотермическом расширении азота при температуре T=280К объем его увеличился в два раза. Определить: 1) совершенную при расширении газа работу A; 2) изменение DU внутренней энергии; 3) количество теплоты Q, полученное газом. Масса азота m=0,2кг.
252. При адиабатном сжатии давление воздуха было увеличено от р1=50кПа до
– 53 –
<vкв> а также средние кинетические энергии <eп> поступательного движения молекулы азота и пылинки.
230. Определить среднюю кинетическую энергию <eп> поступательного движения и <eвр> вращательного движения молекулы азота при температуре Т= 400К. Определить также полную кинетическую энергию Eк молекулы при тех же условиях.
231. Определить молярную массу М двухатомной газа и его удельные теплоемкости, если известно, что разность ср — сV удельных теплоемкостей этого газа равна 260 Дж/(кг×К).
232..Найти удельные ср и сV, а также молярные Сp и СV теплоемкости углекислого газа.
233. Определить показатель адиабаты g идеального газа, который при температуре Т=350К и давлении р = 0,4 МПа занимает объем V = 300л и имеет теплоемкость CV=857 Дж/К.
234. В сосуде вместимостью V=6л находится при нормальных условиях двухатомный газ. Определить теплоемкость СV этого газа при постоянном объеме.
235. Определить относительную молекулярную массу Мr и молярную массу М газа, если разность его удельных теплоемкостей ср — cV=2,08 кДж/(кг×К).
236. Определить молярные теплоемкости газа, если его удельные теплоемкости cV=10,4 кДж/(кг×К) и ср= 14,6 кДж/(кг×К).
237. Найти удельные cV и ср и молярные СV и Сp теплоемкости азота и гелия.
238. Вычислить удельные теплоемкости газа, зная что его молярная масса М=4×10-3 кг/моль и отношения теплоемкостей Ср/СV=1,67.
239. Трехатомный газ под давлением р=240кПа и температуре t=20°C занимает объем V=10л. Определить теплоемкость Ср этого газа при постоянном давлении.
240. Одноатомный газ при нормальных условиях занимает объем V=5л. Вычислить теплоемкость этого газа при постоянном объеме.
241. Найти среднее число <z> столкновений за время t=1с и длину свободного пробега  молекулы гелия, если газ находится под давлением р=2кПа при температуре T =200 К.
молекулы гелия, если газ находится под давлением р=2кПа при температуре T =200 К.
– 12 –
постоянной, т. е.
Р1x+ р2x = p`1x + p`2x, (1),
где р1x и р2x – проекции импульса ящика и тележки с песком в момент падения ящика на тележку; p’1x и p'2x – те же величины после падения ящика. Рассматривая тела системы как материальные точки, выразим в равенстве (1) импульсы тел через их массы и скорости, учитывая, что р2x= 0 (тележка до взаимодействия с ящиком покоилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью и:
m1  1x = (m1+ т2) и, или m1
1x = (m1+ т2) и, или m1  1 cosa= (m1 +m2) и,
1 cosa= (m1 +m2) и,
где  1– модуль скорости ящика перед падением на тележку;
1– модуль скорости ящика перед падением на тележку;  1x =
1x =  1cosa – проекция этой скорости на ось х.
1cosa – проекция этой скорости на ось х.
Отсюда  (2)
(2)
Модуль скорости  определим из закона сохранения энергии:
определим из закона сохранения энергии:
m1gh = ½ m1 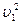 , где h =lsina, откуда
, где h =lsina, откуда
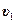 =
= 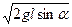 .
.
Подставив выражение 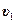 в формулу (2), получим
в формулу (2), получим

После вычислений найдем
 м/c.
м/c.
Пример 4. При выстреле из пружинного пистолета вертикально вверх пуля массой m=20 г поднялась на высоту h=5 м. Определить жесткость k пружины пистолета, если она была сжата на ∆ х=10 см. Массой пружины и силами трения пренебречь.
Решение. Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия E системы в начальном состоянии (в данном случае перед выстрелом)
– 13 –
равна полной энергии Е в конечном состоянии (когда пуля поднялась на высоту h), т.е.
Е1=Е2, или Т1+П1=Т2+П2, (1)
где Т1, Т2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состояниях.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид
П1=П2. (2)
Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высота подъема пули будет отсчитываться от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е. П1= ½ k(∆x) 2, а в конечном состоянии – потенциальной энергии пули на высоте h, т.е. П2=mgh.
Подставив выражения П1 и П2 в формулу (2), найдем ½ k(∆x)2 =mgh, откуда
k=2mgh/x2. (3)
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы (единицу какой-либо величины принято обозначать символом этой величины, заключенным в квадратные скобки):
 (1кг×1м×с-2×1м)/1м2=(1кг×м×с-2)/1м=1Н/м.
(1кг×1м×с-2×1м)/1м2=(1кг×м×с-2)/1м=1Н/м.
Убедившись, что полученная единица является единицей жесткости (1Н/м), подставим в формулу (3) значения величин и произведем вычисления:

Пример 5. Шар массой m1, движущийся горизонтально с некоторой скоростью  , столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
– 52 –
Dр=100кПа. Определить массу т израсходованного кислорода. Процесс считать изотермическим.
220. Определить плотность r водяного пара, находящегося под давлением р=2,5кПа и имеющего температуру Т=250 К.
221. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию <e> молекулы этого газа при температуре Т = 300К, если количество вещества n этого газа равно 0,5 моль.
222. Определить суммарную кинетическую энергию EK поступательного движения всех молекул газа, находящегося в сосуде вместимостью V=3л под давлением p=540 кПа.
223. Количество вещества гелия n= 1,5 моль, температура Т= 120 К. Определить суммарную кинетическую энергию Eк поступательного движения всех молекул этого газа.
224. Молярная внутренняя энергия Um некоторого двухатомного газа равна
6,02 кДж/моль. Определить среднюю кинетическую энергию <eвр> вращательного движения одной молекулы этого газа. Газ считать идеальным.
225. Определить среднюю кинетическую энергию <eвр> одной молекулы водяного пара при температуре Т =500 К.
226. Определить среднюю квадратичную скорость <vкв> молекулы газа, заключенного в сосуд вместимостью V=2л под давлением р=200кПа. Масса газа m=0,3 г.
227. Водород находится при температуре T=300 К. Найти среднюю кинетическую энергию <eвр> вращательного движения одной молекулы, а также суммарную кинетическую энергию Eк всех молекул этого газа; количество водорода n=0,5моль.
228. При какой температуре средняя кинетическая энергия <eп> поступательного движения молекулы газа равна 4,14×10-21 Дж?
229. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6×10-10 г. Газ находится при температуре T=400 К. Определить средние квадратичные скорости
– 51 –
208. В баллоне вместим