МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ОП.02 Электротехника
15.02.07 Автоматизация технологических процессов и производств (по отраслям)
Березники
2019 год
| РАССМОТРЕНО на заседании ЦМК ОП и СЭД протокол № ____ от «____» ________ 20___г. Председатель ЦМК ___________ С.Е. Малинина | УТВЕРЖДЕНО Методическим советом Протокол № ___ от «____» _________ 20___ г. |
Разработал: Чуйнов Владимир Геннадьевич, преподаватель спецдисциплин.
Рецензент: Гагарина Екатерина Борисовна, преподаватель электротехнических дисциплин.
Методические указания рекомендованы к использованию при подготовке к занятиям и самостоятельной работы на уроке студентов очной формы обучения и организации самостоятельной работы студентов заочной формы обучения в период выполнения домашних контрольных работ.
Разработано в соответствии Федеральным государственным образовательным стандартом по специальности среднего профессионального образования 15.02.07 Автоматизация технологических процессов и производств (по отраслям)
Могут быть использованы и для работы при подготовке к занятиям со студентами специальностей 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 08.02.09 Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий, а также может быть использована в дополнительном профессиональном образовании (повышении квалификации и переподготовке работников) и профессиональной подготовке по профессиям рабочих: 19861 Электромонтер по ремонту и обслуживанию электрооборудования.
СОДЕРЖАНИЕ
Введение 4
1 Электрические цепи постоянного тока 5
1.1 Закон Ома 5
1.2 Последовательное соединение потребителей 6
1.3 Параллельное соединение потребителей 6
1.4 Законы Кирхгофа 7
1.5 Потенциальная диаграмма 9
2 Расчет электрических цепей постоянного тока 10
2.1 Метод узловых и контурных уравнений 10
2.2 Метод контурных токов 11
3 Электрические цепи синусоидального тока 11
3.1 Цепь с активным сопротивлением 11
3.2 Цепь с индуктивностью 12
3.3 Цепь с емкостью 13
4 Расчет электрических цепей синусоидального тока 14
4.1 Цепь с активным сопротивлением и индуктивностью 14
4.2 Цепь с активным сопротивлением и емкостью 15
4.3 Неразветвленная цепь с активным сопротивлением, емкостью и индуктивностью 16
5 Разветвленная цепь синусоидального тока 17
5.1 Активный и реактивный токи 17
5.2 Проводимости 17
5.3 Параллельное соединение индуктивности и емкости 18
6 Трехфазные цепи 19
6.1 Соединение обмоток генератора и приемников в звезду 19
6.2 Соединение обмоток генератора и приемников в треугольник 21
7 Задания для самостоятельного решения 22
8 Методические указания к оформлению контрольной работы 28
Список источников 29
ВВЕДЕНИЕ
Основной целью изучения дисциплины «Электротехника» является усвоение электромагнитных законов; изучение электромагнитных процессов, протекающих в электрических цепях, изучение основных принципов построения, функционирования и расчета электрических цепей постоянного и переменного тока, ознакомление с принципом работы электроизмерительных приборов, различных электротехнических устройств.
Задачи изучения МДК 01.01 «Электрические машины» направлены на формирование следующих компетенций:
ПК1.1 – Организовывать и осуществлять эксплуатацию электроустановок промышленных и гражданских зданий.
ПК1.2 – Организовывать и производить работы по выявлению неисправностей электроустановок промышленных и гражданских зданий.
ПК1.3 – Организовывать и производить ремонт электроустановок промышленных и гражданских зданий.
ПК2.1 – Организовывать и производить монтаж силового электрооборудования промышленных и гражданских зданий с соблюдением технологической последовательности.
ПК2.2 – Организовывать и производить монтаж осветительного электрооборудования промышленных и гражданских зданий с соблюдением технологической последовательности.
ПК2.3 – Организовывать и производить наладку и испытания устройств электрооборудования промышленных и гражданских зданий.
ПК3.2 – Организовывать и производить наладку и испытания устройств воздушных и кабельных линий.
ПК3.3 – Организовывать и производить эксплуатацию электрических сетей.
ПК3.4 – Участвовать в проектировании электрических сетей.
ПК4.1 – Организовывать работу производственного подразделения.
ПК4.2 – Контролировать качество выполнения электромонтажных работ.
В результате освоения учебной дисциплины обучающийся должен уметь:
- выполнять расчеты электрических цепей;
- выбирать электротехнические материалы на основе анализа их свойств для конкретного применения;
- пользоваться приборами и снимать их показания;
- выполнять поверки амперметров, вольтметров и однофазных счетчиков;
- выполнять измерения параметров цепей постоянного и переменного ток
В результате освоения учебной дисциплины обучающийся должен знать:
- основы теории электрических и магнитных полей;
- методы расчета цепей постоянного, переменного однофазного и трехфазного токов;
- методы измерения электрических, неэлектрических и магнитных величин;
- схемы включения приборов для измерения тока, напряжения, энергии, частоты, сопротивления изоляции, мощности;
- правила поверки приборов: амперметра, вольтметра, индукционного счетчика;
- классификацию электротехнических материалов, их свойства, область применения.
1 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.1 Закон Ома
Ток, проходящий по участку цепи, прямо пропорционален напряжению U, приложенному к этому участку, и обратно пропорционален его сопротивлению R.

где U – напряжение цепи, В;
I – ток в цепи, А;
R – сопротивление цепи, Ом.
Закон Ома для полной цепи будет выглядеть следующим образом:

где R0 – сопротивление источника, Ом;
R – сопротивление потребителя, Ом;
Е – электродвижущая сила, В.

Рисунок 1.1 – Замкнутая электрическая цепь
Электрическое сопротивление проводника:
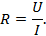
Единицей измерения сопротивления является Ом. Сопротивление зависит от длины проводника l, площади поперечного сечения S и материала проводника ρ.
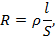
где ρ – удельное сопротивление, Ом·мм2;
l – длина проводника, м;
S – площадь поперечного сечения, мм2.
Величину, обратную удельному сопротивлению называют удельной проводимостью.
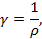
где γ – удельная проводимость, (м/Ом∙мм2).
Величину обратную сопротивлению называют проводимостью

где G – проводимость, См.
1.2 Последовательное соединение потребителей.
Последовательным соединением участков электрической цепи называют соединение, при котором через все участки цепи проходит один и тот же ток.

Рисунок 1.2 – Последовательное соединение потребителей
При последовательном соединении потребителей с сопротивлениями R1, R2 и R3 напряжение на их зажимах равно

Для данной цепи можно записать


Откуда

Таким образом, общее эквивалентное сопротивление последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.
Ток в цепи последовательно включенных сопротивлений определяется выражением

1.3 Параллельное соединение потребителей
Параллельным соединением участков электрической цепи называется соединение, при котором все участки цепи присоединяются к одной паре узлов, т.е. находятся под действием одного и того же напряжения.
При параллельном соединении сопротивлений токи потребителей соответственно равны


Рисунок 1.3 – Параллельное соединение потребителей
Ток в неразветвленной части цепи будет равен


Тогда

Общее сопротивление параллельно включенных сопротивлений (потребителей) равна сумме обратных величин сопротивлений этих потребителей.
Для трех параллельно включенных потребителей общее их сопротивление будет находиться следующим образом
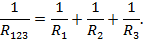
1.4 Законы Кирхгофа
В схемах электрических цепей можно выделить характерные элементы: ветвь, узел, контур.
Ветвью электрической цепи называется ее участок, на всем протяжении которого величина тока имеет одинаковое значение.
Узлом электрической цепи (узловой точкой) называется место соединения электрических ветвей. В узловой точке сходятся как минимум три ветви.

Рисунок 1.4 – Узел электрической цепи
Контуром электрической цепи называют замкнутое соединение, в которое могут входить несколько ветвей.

Рисунок 1.5 – Контур электрической цепи
Ветви, содержащие источник электрической энергии, называются активными, а ветви, не содержащие источников, называются пассивными.
Первый закон Кирхгофа. В разветвленной цепи ток в различных ветвях может иметь различное значение. Сумма токов, входящих в узловую точку разветвленной цепи должна быть равна сумме токов, выходящих из этой точки.
Для узловой точки А (см. рисунок 1.4) можно записать

или

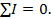
Токи, входящие в узел принято считать положительными, а выходящие из узла - отрицательными.
Первый закон Кирхгофа формулируется следующим образом: алгебраическая сумма токов в ветвях, соединенных в один узел, равна нулю.
Второй закон Кирхгофа устанавливает зависимость между ЭДС и падением напряжения в замкнутом контуре любой электрической цепи. Для данного контура можно записать следующее выражение
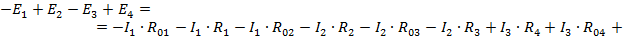

которое и будет являться вторым законом Кирхгофа. Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падения напряжений на всех участках этой цепи.

Для определения знаков в алгебраической сумме направление обхода контура выбирается произвольно. ЭДС источника, совпадающий с выбранным направлением обхода контура, считается положительной, а не совпадающая – отрицательной. Падение напряжения на сопротивлении считается положительным, если ток, протекающий через него совпадает с выбранным направление обхода контура, или отрицательным – если не совпадает.
1.5 Потенциальная диаграмма
При изучении и расчете электрических цепей необходимо определить потенциалы отдельных точек и построить потенциальную диаграмму.

Рисунок 1.6 – Неразветвленная электрическая цепь
На участке AB точка B имеет положительный потенциал, а точка A отрицательный потенциал, поэтому
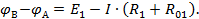
Так как источник работает в режиме генератора, то

На участке BC точка В имеет положительный потенциал, а точка С отрицательный, поэтому

Так как источник работает в режиме потребителя, то

Таким образом, потенциал точки D можно записать

если обходить цепь по направлению тока, или

если обходить цепь против направления тока.
Отсюда можно создать следующее правило: если обходить цепь или участок цепи по направлению тока, тот потенциал в каждой точке определяется потенциалом предыдущей точки плюс ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя и минус падение напряжения на участке между точками цепи. При обходе контура против направления тока знаки ЭДС и падения напряжения изменяются на противоположные.
Это правило удобно применять в тех случаях, когда в цепи имеются участки с несколькими источниками.
Потенциальная диаграмма представляет собой график зависимости потенциалов точек от величины сопротивлений участков между этими точками.
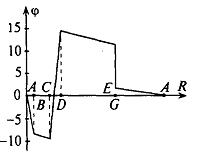
Рисунок 1.7 – Потенциальная диаграмма
Для построения потенциальной диаграммы одну из точек электрической цепи условно заземляют (потенциал принимают равным нулю), а потенциалы остальных точек равны напряжению между ними и заземленной точкой.
2 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
2.1 Метод узловых и контурных уравнений
Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравнений по законам Кирхгофа. При составлении системы уравнений должно учитываться следующее.
1. Число уравнений равно числу токов в цепи. Направление токов в ветвях выбирается произвольно.
2. По первому закону Кирхгофа составляется на одно уравнение меньше, чем узловых точек в схеме.
3. Остальные уравнения составляются по второму закону Кирхгофа.

Рисунок 2.1 – Сложная электрическая цепь
В рассматриваемой цепи имеется пять ветвей, следовательно, пять различных токов, поэтому для расчета необходимо составить пять уравнений. Так как в цепи три узловых точек, то по первому закону Кирхгофа составляется два уравнения. Остальные три уравнения составляются по второму закону Кирхгофа (внутренним сопротивлением источника тока пренебрегаем). Обход по часовой стрелке.
1) 
2) 
3) 
4) 
5) 
2.2 Метод контурных токов
При расчете сложных цепей методом узловых и контурных уравнений приходится решать систему из большого количества уравнений, что значительно затрудняет вычисления. Задачу можно упростить, если воспользоваться методом контурных токов.
Суть метода состоит в том, что в схеме выделяются независимые контуры, в каждом из которых произвольно направлены контурные токи.

Рисунок 2.2 – Сложная электрическая цепь
Отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.


Для определения контурных токов составляют уравнения по количеству равным числу независимых контуров. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров. Для данной схемы (см. рисунок 2.2) необходимо составить четыре уравнения. Со знаком «плюс» записываются ЭДС и падения напряжения, действующие в направлении контурного тока, со знаком «минус» - направленные против контурного тока.

Решением системы уравнений вычисляются значения контурных токов, которые и определяют действительные токи в каждой ветви схемы.
3 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.1 Цепь с активным сопротивлением
Если к активному сопротивлению R приложено синусоидальное напряжение, то и ток в этой цепи изменяется по синусоидальному закону
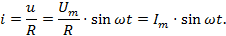
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением.


Рисунок 3.1 – Векторная диаграмма для цепи с активным сопротивлением
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид
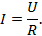
Величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома
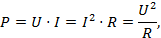
где Р – активная мощность, Вт.
3.2 Цепь с индуктивностью
Если в цепи с катушкой индуктивности L проходит синусоидальный ток, то этот ток создает в катушке синусоидальный магнитный поток Ф, который индуктирует в катушке ЭДС самоиндукции

Эта ЭДС достигает своего амплитудного значения
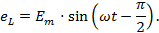
Таким образом, ЭДС самоиндукции в цепи с индуктивностью, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90º.
Напряжение, приложенное к цепи с индуктивностью

Напряжение достигает своего амплитудного значения

Таким образом, напряжение, приложенное к цепи с индуктивностью, как и ток в этой цепи, изменяется по синусоидальному закону, но опережает ток по фазе на угол 90º.

Рисунок 3.2 – Векторная диаграмма для цепи с индуктивностью
Математическое выражение закона Ома для цепи переменного тока с индуктивностью имеет вид

где ω∙L=XL – индуктивное сопротивление, Ом.
Таким образом

Закон Ома для цепи с индуктивностью
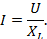
Величина реактивной мощности в цепи с индуктивностью определяется выражением

где QL – реактивная мощность, Вар.
3.3 Цепь с емкостью
Если к конденсатору емкостью С приложено синусоидальное напряжение, то вцепи конденсатора проходит ток

Ток в цепи конденсатора достигает своего амплитудного значения

Тогда

Ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90º.

Рисунок 3.3 – Векторная диаграмма для цепи с емкостью
Математическое выражение закона Ома для цепи переменного тока с емкостью

где  – емкостное сопротивление, Ом.
– емкостное сопротивление, Ом.

Тогда закон Ома для цепи переменного тока с конденсатором можно записать
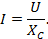
Величина реактивной мощности в цепи конденсатора определяется выражением

4 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
4.1 Цепь с активным сопротивлением и индуктивностью

Рисунок 4.1 – Цепь с активным сопротивлением и индуктивностью и ее векторная диаграмма
Из векторной диаграммы (см. рисунок 4.1) видно, что напряжение, приложенное к катушке, опережает по фазе ток на угол φ. Где φ – это сдвиг фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника по векторной диаграмме (см. рисунок 4.1) можно найти напряжение.

Отсюда можно найти ток

Это равенство является математическим выражением закона Ома для цепи синусоидального тока с активным и индуктивным сопротивлением в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным сопротивлением цепи синусоидального тока.

где Z – полное сопротивление цепи синусоидального тока, Ом.
Тогда закон Ома для любой цепи переменного тока можно записать

4.2 Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью C протекает синусоидальный ток, то он создает падение напряжения на активном сопротивлении

и на емкостном сопротивлении


Рисунок 4.2 – Цепь с активным сопротивлением и емкостью и ее векторная диаграмма
Напряжение сети изменяется по синусоидальному закону, как и ток, и отстает по фазе от тока на угол φ<90º.

Действующее значение напряжения, приложенного к этой цепи, определяется по векторной диаграмме (см. рисунок 4.2)
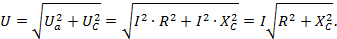
Откуда математическое выражение закона Ома для этой цепи
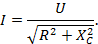
4.3 Неразветвленная цепь с активным сопротивлением, емкостью и индуктивностью
Если в неразветвленной цепи с R, L и C протекает синусоидальный ток, то он создает падение напряжения на всех участках цепи.



Мгновенное значение напряжения цепи определяется по формуле


Рисунок 4.3 – Цепь с активным сопротивлением, емкостью и индуктивностью и ее векторная диаграмма
Так как в рассматриваемой цепи включены два реактивных сопротивления, то возможны три режима работы цепи:
1) XL˃XC;
2) XL<XC;
3) XL=XC.
Знак перед углом сдвига фаз зависит от режима работы цепи. Если в рассматриваемой цепи преобладает индуктивное сопротивление, тот цепь имеет индуктивный характер и напряжение опережает ток по фазе.
Если в цепи преобладает емкостное сопротивление, то цепь имеет емкостной характер и напряжение отстает от тока по фазе.
Из векторной диаграммы (см. рис 4.3) следует

Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкостью

где полное сопротивление цепи

Знак и значение угла φ можно определить следующим образом
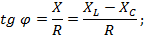

Если XL˃XC, то угол φ положительный, если XL<XC, то угол φ отрицательный.
5 РАЗВЕТВЛЕННАЯ ЦЕПЬ СИНУСОИДАЛЬНОГО ТОКА
5.1 Активный и реактивный токи
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное и индуктивное сопротивление, приложено синусоидальное напряжение, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол φ. Векторная диаграмма в этом случае будет выглядеть следующим образом

Рисунок 5.1 – Треугольник токов
Ток в цепи I раскладывается на две составляющие, одна из которых Ia совпадает с напряжением, а друга IР – сдвинута на 90º.
Составляющая тока Ia называется активной составляющей или активным током. Составляющая тока IP называется реактивной составляющей или реактивным током.
Соотношение между токами определяются из треугольника токов (см. рисунок 5.1).
5.2 Проводимости
Из треугольника токов (см. рисунок 5.1) следует
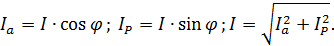
Тогда

где g – активная проводимость цепи, См.
величина реактивного тока определяется выражением

где b – реактивная проводимость цепи, См.
Величина полного тока цепи равна

где y – полная проводимость цепи, См.
5.3 Параллельное соединение индуктивности и емкости
Если к источнику синусоидального напряжения подключить параллельно катушку с активным и индуктивным сопротивлением и конденсатор с активным и емкостным, то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону.

Рисунок 5.2 – Параллельное соединение индуктивности и емкости
Действующие значения этих токов будут соответственно равны


Ток в этой цепи равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе

Для определения этого тока строится векторная диаграмма.

Рисунок 5.3 – Векторная диаграмма цепи с параллельным соединением индуктивности и емкости
Из векторной диаграммы следует

Таким образом, ток в неразветвленной цепи определяется произведением напряжения и полной проводимости цепи.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток в цепи отстает от напряжения, то цепь индуктивного характера, если же ток опережает напряжение, то цепь емкостного характера.
6 Трехфазные цепи
6.1 Соединение обмоток генератора и приемников в звезду.
Звезда – это такое соединение, когда к началам обмоток генератора А, В, С присоединяют три линейных провода, идущих к приемнику, а концы обмоток X, Y, Z соединены в узел, называемый нейтральной или нулевой точкой.
В четырехпроводной системе к этой точке присоединен нейтральный, или нулевой, провод (см. рисунок 6.1), в трехпроводной системе он отсутствует (см. рисунок 6.2).

Рисунок 6.1 – Четырехпроводная схема соединения обмоток генератора и приемника

Рисунок 6.2 – Трехпроводная схема соединения обмоток генератора и приемника
Напряжение между началами и концами фаз генератора или между линейными проводами и нейтральным (нулевым) проводом называют фазным напряжением.
Напряжение между любыми двумя линейными проводами называют линейным напряжением.
Токи, проходящие по линейным проводам, называют линейными и обозначают IА, IВ, IС. Токи, проходящие в фазах, называют фазными.
При соединении в «звезду» линейные токи равны соответствующим фазным токам.

где IЛ, IФ – линейный и фазный токи, А.

Рисунок 6.3 – Трехфазная система соединенная «звездой»
Для симметричной нагрузки

где UЛ, UФ – линейное и фазное напряжения, В.
При соединении приемников энергии в «звезду» трехфазная цепь может быть четырехпроводной (см. рисунок 6.1) и трехпроводной (см. рисунок 6.2).

где UA, UB, UC – действующие значения фазных напряжений, В,
ZA, ZB, ZC – полные сопротивления фаз приемников, Ом.
В четырехпроводной системе ток в нейтральном проводе равен векторной сумме токов отдельных фаз.
В четырехпроводной системе ток в нейтральном проводе равен векторной сумме токов отдельных фаз.

В четырехпроводной трехфазной цепи при равномерной нагрузке, т.е. равенстве полных сопротивлений приемников, ток в нейтральном проводе равен нулю.
Активная мощность всей цепи при неравномерной нагрузке равна сумме активных мощностей отдельных фаз.

где P – активная мощность всей цепи, Вт,
PA, PB, PC – активные мощности фаз, Вт.



Реактивная мощность всей цепи при неравномерной нагрузке равна алгебраической сумме реактивных мощностей отдельных фаз.

где Q – реактивная мощность всей цепи, Вар,
QA, QB, QC – реактивные мощности фаз, Вар.



Полная потребляемая мощность цепи при неравномерной нагрузке

где S – полная мощность всей цепи, ВА.
При симметричной системе напряжений и равномерной нагрузке мощности всей цепи
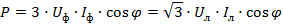



Рисунок 6.4 – Топографическая диаграмма трехфазной цепи соединенной в «звезду» с симметричной нагрузкой
6.2 Соединение обмоток генератора и приемников в треугольник.

Рисунок 6.4 – Трехфазная система соединенная «треугольником»
Фазные напряжения на генераторе являются и линейными

При соединении приемника энергии в «треугольник» нагрузку подключают непосредственно к линейным проводам, поэтому линейные напряжения являются одновременно и фазными для приемников.
При равномерной нагрузке и симметричной системе напряжений при соединении потребителей треугольником линейный ток в трехфазной цепи равен
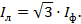

Рисунок 6.5 – Топографическая диаграмма трехфазной цепи соединенной в «треугольник» с симметричной нагрузкой
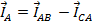
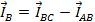

7 Задания для самостоятельного решения