Наибольшее и наименьшее значения функции двух переменных в области.
Так же, как в случае функции одной переменной, заданной на отрезке, функция двух переменных, заданная в замкнутой области, достигает своих наибольшего и наименьшего значений либо в критических точках, лежащих в заданной области, либо в граничных точках области. Трудность этого случая в том, что у области на плоскости, имеется бесконечное множество граничных точек.
П р и м е р. Найти наибольшее и наименьшее значения функции
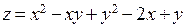в треугольнике, образованном прямыми 
.
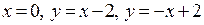Прежде всего, найдем критические точки заданной функции, решив систему
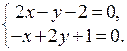
Данная система имеет единственное решение, и мы получаем критическую точку (1,0). Эта точка лежит внутри заданной области, поэтому мы вычисляем в этой точке значение функции: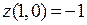 
.
Теперь переходим к граничным точкам. Заданная область имеет 3 прямолинейных граничных участка: 1)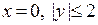 
, 2) 
,
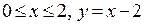3) 
.
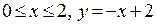На участке 1)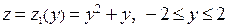 
. Функция 
на отрезке
[-2,2] принимает наибольшее значение, равное 6, в точке 2 (конец отрезка), и наименьшее значение, равное -1/4, в критической точке -1/2.
На участке 2)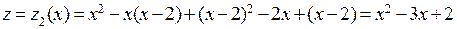 
,
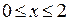. Функция 
принимает на отрезке [0,2] наибольшее значение, равное 2, в точке 0 (конец отрезка), и наименьшее значение, равное -1/4, в критической точке 3/2. На участке 3)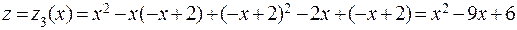 
, 
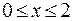. Функция 
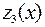принимает на отрезке [0,2] наибольшее значение, равное 6, в точке 0 (конец отрезка), и наименьшее значение, равное -3/4, в критической точке 3/2.
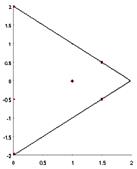
Получив значения в критической точке и наибольшие и наименьшие значения на отрезках границы (-1, 6, -1/4, 2, -3/4), мы выбираем среди них наибольшее и наименьшее. Это значения 6 (наибольшее значение данной функции в заданном треугольнике) и -1 (наименьшее значение данной функции в заданном треугольнике). Трехмерное изображение соответствующей поверхности выглядит следующим образом.
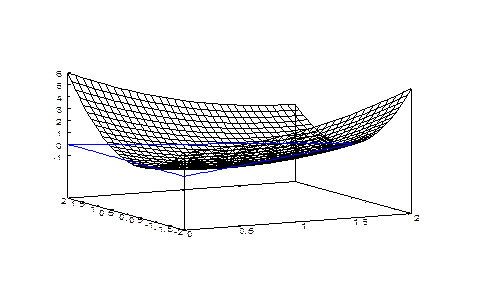
Нетрудно заметить, что наибольшие трудности в вопросах выявления наибольших и наименьших значений в области связаны с проблемами нахождения соответствующих значений на участках границы области.
Условный экстремум функции нескольких переменных
Представим, что мы решаем задачу нахождения наибольшего и наименьшего значений функции 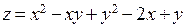не внутри треугольной области, как в предыдущем параграфе, а в области 
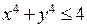. После нахождения критических точек внутри круга мы должны найти наибольшие и наименьшие значения на границе – кривой 
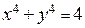. Если решать задачу по аналогии с предыдущим решением, очевидно, что после выражения одной из переменных через другую в уравнении границы и подстановки в выражение исходной функции мы получим довольно сложное представление исходной функции на граничной окружности: 
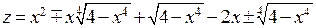. Более того, граничная кривая может иметь такое уравнение, из которого невозможно явно выразить одну переменную через другую.
Задачи нахождения наибольших и наименьших значений функции при выполнении условий относительно переменных называются задачами нахождения условных экстремумов. В приведенном примере условием является равенство .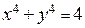
Лагранжем был разработан метод решения таких задач. Итак, пусть нужно найти наибольшие и наименьшие значения функции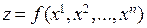 
при выполнении условия 
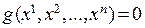. Для этого следует построить новую функцию, называемую функцией Лагранжа
.
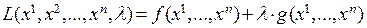Число переменных функции Лагранжа на 1 больше, чем число переменных исходной функции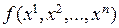 
благодаря введению параметра 
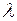. Далее ищутся критические точки функции 
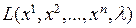из системы
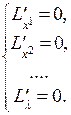
Среди полученных критических точек будут точки, дающие условные экстремумы.
П р и м е р.Найти условныеэкстремумы функции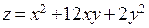 
при условии 
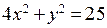. Рассмотрим функцию Лагранжа 
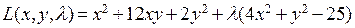и найдем ее критические точки из системы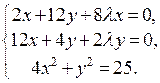 
Рассмотрим одновременно два первых уравнения системы в виде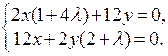 
Если решать эту систему относительно переменных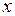 
и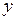 
, то, применяя правило Крамера, получим следующее: если главный определитель системы отличен от нуля, то система имеет единственное решение 
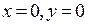. Однако это решение противоречит третьему уравнению исходной системы. Поэтому единственная возможность получить ненулевые решения системы из двух первых уравнений – это приравнять главный определитель системы из двух уравнений нулю: 
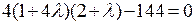. Следовательно, 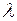– корень квадратного уравнения 
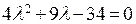. Решив это уравнение, получим два значения: 
и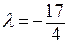 
.
При система из первых двух уравнений превращается в одно соотношение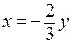 
. Подставляя это соотношение в третье уравнение, получим критические точки 
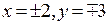. Значение исходной функции в этих точках: 
.
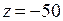При 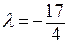система из первых двух уравнений превращается в соотношение 
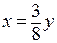. Подставляя это соотношение в третье уравнение, получим критические точки 
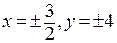. Значение исходной функции в этих точках: 
.
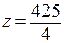Таким образом, условным минимумом исходной функции является значение -50, условным максимумом является значение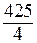 
.
Задачи условного экстремума могут решаться и при нескольких условиях.
Пусть нужно найти наибольшие и наименьшие значения функции 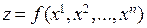при выполнении услови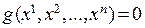й и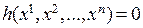 
. В таком случае число переменных функции Лагранжа увеличивается на 1, и функция Лагранжа будет иметь вид
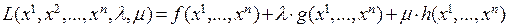. Дальше, как и в предыдущем случае, ищутся критические точки функции Лагранжа, которые являются точками условного экстремума исходной функции.