Длина первой линии l 1 = 100 км, длины линий 2 и 3 равны l 2 = l 3 = 50 км. Будем рассматривать момент времени, когда отраженные от нагрузки второй линии П2 волны прошли расстояние s = 40 км. К этому моменту времени волны, возникшие в начале первой линии, пройдут расстояние L = l 1+ l 2+ s = 190 км. При одинаковой скорости распространения волн во всех линиях для этого потребуется время t = L / v = 190/300000 = 6.3.·10-4 с. Следовательно, время «существования» прямых и отраженных волн в линии 1 составит t p = 6.3·10-4 с.
При частоте источника И1 f =50 Гц (ω ≈314 рад/с) и амплитудном значении Em = 180 кВ получим:
– в момент замыкания ключа
e(0)= 
=180 кВ=180 кВ
– при t = t р
e(
)= 
= 
кВ
т.е. относительное изменение входного напряжения составит
2 %
Поэтому можно считать, что напряжение на зажимах первой линии не меняется за время рассмотрения переходного процессы и равно U 0 = const.
Определение постоянного напряжения U 0
Напряжение U 0 представляет собой напряжение прямой (падающей) волны в 1-й линии 
= 
.
Ток
Расчет переходного процесса в системе линий
Для каждой линии введем свою локальную систему координат: x – от начала линии к её концу; x ' – от конца линии к началу. Прямые (падающие) (ϕ1, ϕ2, ϕ3) волны напряжения и тока в каждой из линий распространяются в направлении оси x соответствующей линии, об-ратные, или отраженные, (ψ1, ψ2, ψ3) – в направлении оси x '. Будем обозначать напряжения и токи в начале линии дополнительным ин-дексом «0», а в конце линии – индексом «l ».
Схема замещения для расчета процессов на подстанции П1
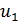= 2 
= 
= 2 U 0 = 
В;
R 2 = 120 Ом;
C1= 0.1 мкФ;
80 Ом;
= 
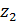= 300 Ом;
= Z 3 = 270 Ом.
Отсчет времени t ' ведется от момента прихода волны ϕ1 к входным зажимам подстанции П1 1'-1'. В этот момент времени возникает отраженная волна в линии 1 и преломленные (падающие) волны в ли-ниях 2 и 3.
Расчет переходного процесса
Без составления дифференциального уравнения
Искать будем ток 
:
Рассмотрим цепь до коммутации 
:
Источник напряжения еще не подключен.
Рассмотрим цепь непосредственно после коммутации (t = +0):
Находим постоянную времени (ключ замкнут, источник напряжения представляет собой провод):
В таком случае 
.
Установившийся режим 
:
В установившемся режиме конденсатор представляет собой разрыв.
Входной ток 
А
Найдем постоянную интегрирования:
, откуда 
A
Общее выражение запишется в виде: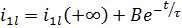 
Подставив значения, получим:
A
Найдем напряжение на конденсаторе:
Напряжение на конденсаторе равно напряжениям на зажимах 2-2 и 3-3, тогда:
Теперь найдем падающие волны напряжений во второй и третьей линиях:
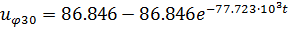кВ
кВ
Теперь можем найти падающие волны токов во второй и третьей линиях:
Найдем отраженную волну тока в первой линии:
Отсюда: 
А
Найдем отраженную волну напряжения в первой линии:
кВ
Отсюда напряжение на конце первой линии:
кВ
Зависимости от времени t' напряжений и токов на входных и выходных зажимах подстанции П1 (зажимы 1'-1' и 2(3) – 2(3)).
Графики напряжения и тока, отраженных от подстанции П1 (ψ1l на зажимах 1'-1') и преломленных через подстанцию в линию 2 (φ20 на зажимах 2'-2') и в линию 3 (φ30 на зажимах 3'-3')
