Подсчёт нагрузки на 1м длинны пристенного ребра приведен в таблице 1.3
Таблица 1.3- Нагрузка на 1м длинны пристенного ребра.
| Вид нагрузки и подсчёт | Нормативная
нагрузка
| Частный
коэффициент
по нагрузке,
| Расчётная
нагрузка,
|
1.Постоянная
1.1 Собственный вес ребра
| 0,37 | 1,15 | 0,43 |
1.2 Собственный вес плиты
2. Переменная
| 1,18 1,94 | 1,15 1,5 | 1,36 2,91 |
| Итого (gk+qk)1= | 3,49 | (gd+qd)1= | 4,70 |
Расчётная схема пристенного ребра показано на рисунке 2.5
Рисунок 2.5 Расчётная схема пристенного ребра.
Форму сечения пристенного ребра принимаем тавровую с размерами:
Расчётный изгибающий момент лобового ребра:
(1.20)
Расчётная поперечная сила:
(1.21)
Расчёт рабочей арматуры пристенного ребра
Для сечения с одиночным армированием проверяем условие, определяющее положение нейтральной оси. Предполагаем, что нейтральная ось проходит по нижней грани, и определяем область деформирования для прямоугольного сечения шириной 
.
что указывает на то, что сечение находится в области деформирования 2.
По формуле 6.6(3) находим величину изгибающего момента, воспринимаемого бетоном, расположенным в пределах полки:
Поскольку выполняется условие, 
нейтральная ось располагается в пределах полки в связи с этим дальнейший расчёт производим как для прямоугольного сечения имеющего размеры 
Определяем коэффициент 
по формуле 1.3
По таблице 6.7(3) при 
0,025 определяем, что сечение находится в области деформирования 1а, отсюда 
Находим величину требуемой площади растянутой арматуры по формуле 1.7
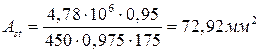
Минимальное значение требуемой площади поперечного сечения арматуры:
По таблице сортамента арматуры принимаем один стержень диаметром 10 класса S400 для которого 
.
1.1.4.2 Расчёт прочности пристенного ребра на действие поперечной силы 
.
Поперечная сила от полной расчётной нагрузки 
с учётом коэффициента 
Расчёт производим на основе расчётной модели наклонных сечений.
Проверим прочность пристенного ребра по наклонной полосе между наклонными трещинами в соответствии с условием (1.12).
Определяем 
по формуле (1.13):
по формуле (1.14), 
по формуле (1.15)
где 
- площадь сечения одного поперечного стержня 
6мм класса S240.
принимаем на опорном участке шаг стержней равный 100мм, на остальном участке пролёта 
.
определяем по таблице 11.2(1)
коэффициент, определяемый по формуле (1.16)
;
Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.
По формуле (1.17) определяем поперечную силу, воспринимаемую бетоном и поперечной арматурой.
(1.17)
где 
- коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах и определяемый по формуле (1.18)
При этом 
.
Для расчёта 
принимаем 
210мм
принимаем 
=0,5
- усилие в поперечных стержнях на единицу длины элемента, определяемое по формуле (1.19),
где 
=157МПа- расчётное сопротивление поперечной арматуры (таблица 6.5(1)).
Следовательно, прочность на действие поперечной силы по наклонной трещине обеспечена.
Поперечные ребра армируем конструктивно с помощью каркасов Кр-3 с рабочей арматурой, требуемая минимальная площадь поперечного сечения которой равна: 
Принимаем диаметр рабочей арматуры равным 10мм класса S400.