полная система уравнений Максвелла в дифференциальной и интегральной формах имеет вид:
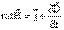
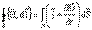
– обобщенный закон Био–Савара–Лапласа;
; 
– закон Фарадея;
; 
– теорема Гаусса; 
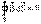– отсутствие магнитных зарядов;
, 
, 
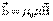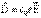1) Мы знаем теорему о циркуляции вектора напряжённости магнитного поля:
,
но: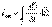 
; т.е. 
, тогда
 ,
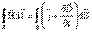| (7.3.1) |
Это уравнение является обобщением закона Био–Савара–Лапласа и показывает связь между полным током и порождаемым им магнитным полем.
В дифференциальной форме это уравнение Максвелла выглядит так:
2) Рассматривая явление электромагнитной индукции, мы сделали вывод, что ЭДС индукции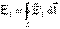 
. Перейдем от вихревого электрического поля к магнитному:
 ,
| (7.3.2) |
Это уравнение описывает явление электромагнитной индукции (закон Фарадея) и устанавливает количественную связь между электрическими и магнитными полями: переменное электрическое поле порождает переменное магнитное поле. В этом физический смысл уравнения.
В дифференциальной форме это уравнение выглядит так:
Различие в знаках этого уравнения Максвелла соответствует закону сохранения энергии и правилу Ленца. Если бы знаки при 
и 
были одинаковы, то бесконечно малое увеличение одного из полей вызвало бы неограниченное увеличение обоих полей, а бесконечно малое уменьшение одного из полей, приводило бы к полному исчезновению обоих полей. То есть различие в знаках является необходимым условием существования устойчивого ЭМП.
3) Ещё два уравнения выражают теорему Остроградского–Гаусса для электрического и магнитного полей (статических полей)
 ,
| (7.3.3) |
Поток вектора электрического смещения 
через замкнутую поверхность S равен сумме зарядов внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора и 
начинаются и заканчиваются на зарядах.
В дифференциальной форме
где 
4) И для магнитного поля
 ,
| (7.3.4) |
Это уравнение выражает то свойство магнитного поля, что линии вектора магнитной индукции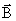 
всегда замкнуты и что магнитных зарядов нет.
В дифференциальной форме
 ,
| (7.3.5) |
5, 6, 7) Наконец надо помнить, что величины, входящие в эти четыре уравнения не независимы, и между ними существует связь:
 ,
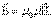| (7.3.6) |
 ,
| (7.3.7) |
 ,
| (7.3.8) |
здесь σ – удельная проводимость, 
– плотность сторонних токов.
Эти уравнения называются уравнениями состояния или материальными уравнениями. Вид этих уравнений определяется электрическими и магнитными свойствами среды. В общем случае уравнения состояния очень сложны и нелинейны.
.
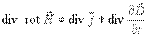В векторном анализе известен результат (его можно проверить непосредственным вычислением!)
.
.
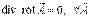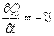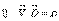
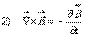
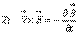
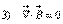
Теперь делаем следующее: уравнение 2) я скалярно умножу на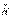 
, уравнение 4) я скалярно умножу на 
: 
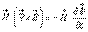
Теперь из второго уравнения вычтем первое:
Для однородного диэлектрика 
. Это были наводящие соображения, на самом деле, в общем случае 
, точно также 
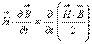. Тогда уравнение приобретает такой вид: 
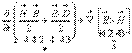или
.
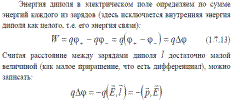
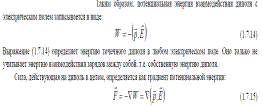
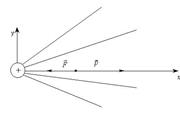
(рис. 2.3). На рис 2.3 
- радиус-вектор точки расположения отрицательного заряда диполя, а 
- радиус-вектор точки расположения положительного заряда диполя. Суммарная сила, действующая на рассматриваемую систему электрических зарядов описывается выражением:
.
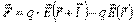С учетом приведенного выше соотношения (2.15) получим
.
Для момента сил, действующих на рассматриваемую систему электрических зарядов, относительно начала координат имеем:
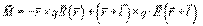
и в полученном соотношении пренебречь членом с сомножителем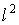 
из-за его малости, приходим к результату: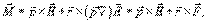
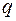, движущийся со скоростью 
в магнитном поле
, (18)
где 
– вектор магнитной индукции поля.
· Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
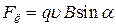, (19)
где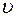 
– модуль вектора скорости; 
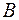– модуль вектора индукции магнитного поля, 
– угол между векторами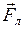 
определяется по правилу левой руки:
если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции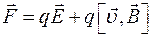 
,(20)
формула (20) называется формулой Лоренца.
.
В векторном анализе известен результат (его можно проверить непосредственным вычислением!)
. Это были наводящие соображения, на самом деле, в общем случае 
.
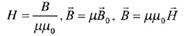ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.