Силы инерции.
Сформулируем, уже известный нам, первый закон Ньютона: существует такая система отсчета, относительно которой тело, не подверженное действию других тел, сохраняет состояние покоя, либо равномерного прямолинейного движения.
Такую систему отсчета называют инерциальной (ИСО).
Любая система отсчета, движущаяся относительно ИСО равномерно и прямолинейно, также будет ИСО, а система отсчета, движущаяся относительно ИСО с ускорением, называется неинерциальной (НСО).
Законы Ньютона справедливы только в ИСО.
Так, второй закон Ньютона для частицы массой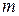 
в ИСО имеет вид
.
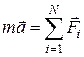Здесь все силы – это силы взаимодействия частицы с окружающими телами, которые и определяют ускорение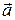 
.
Обозначим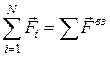 
, тогда 
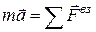. (1)
Относительно всех ИСО данная частица движется с одинаковым ускорением.
Любая НСО сама движется относительно ИСО с некоторым ускорением, поэтому ускорение тела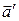 
в НСО отлично от ускорения тела 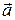в ИСО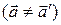 
.
Следовательно, уравнение (1) в том виде, в каком оно записано, несправедливо для частицы в НСО. Однако 2-ой закон Ньютона применим для описания движения в НСО, если ввести в рассмотрение особые силы – силы инерции и учитывать их в уравнении движения.
Второй закон Ньютона или динамическое уравнение движения частицы в НСО будет иметь формально аналогичный вид, как и для частицы в ИСО, но с добавлением сил инерции
,
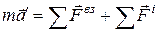где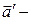 
ускорение частицы в НСО; 
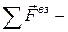геометрическая сумма всех сил взаимодействия данной частицы с другими телами; 
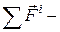геометрическая сумма всех сил инерции, действующих на частицу в данной НСО.
Силы инерции обусловлены характером движения НСО, относительно ИСО.
Для того чтобы разобраться какие именно силы инерции будут действовать на движущуюся частицу в различных НСО, рассмотрим три случая движения НСО относительно ИСО.
ИСО будем называть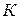 
- системой, а НСО – 
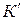- системой.
Рассмотрим первый случай.
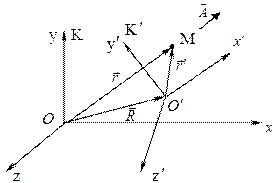Пусть 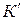-система движется относительно 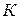-системы поступательно с ускорением 
.
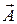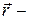радиус-вектор частицы М в 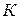-системе; 
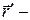радиус-вектор частицы М в 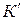-системе.
Как видно из рис.1, в любой момент времени эти радиус-векторы связаны соотношением
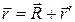, (2)
где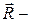 
радиус-вектор начала координат 
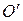системы 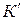относительно начала координат 
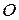системы .
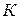Продифференцируем уравнение (2) по времени (в нерелятивистской механике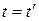 
), получим
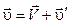, (3)
т.к. ориентация осей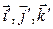 
системы 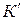остается неизменной.
В (3)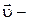 
скорость частицы относительно ; 
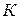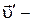скорость частицы относительно ; 
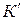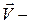скорость 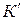относительно .
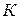Продифференцируем уравнение (3) по времени, получим
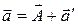, (4)
где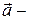 
ускорение частицы относительно ; 
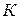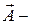ускорение 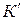-системы относительно 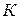-системы; 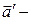ускорение частицы относительно .
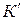Из (4)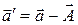 
.
Умножим это выражение на массу частицы 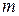, получим
,
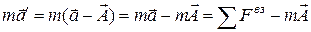где .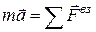
Обозначим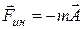 
. (5)
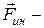сила инерции, обусловленная ускоренным поступательным движением 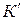-системы относительно 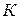- системы (поступательная сила инерции).
Тогда
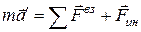, (6)
(6) – динамическое уравнение движения частицы в НСО в первом случае.
Пример:
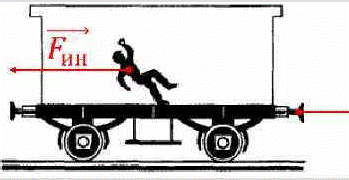
Рассмотрим второй случай.
Пусть 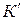-система вращается с постоянной угловой скоростью 
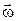вокруг оси 
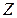, неподвижной в 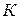- системе. Совместим точк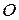и и .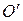
Если частица (шарик) неподвижна в 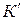-системе, то на нее будет действовать центробежная сила инерции
, (7)
где 
центростремительное ускорение;
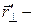расстояние от точки 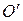до шарика.
Если же частица (шарик) движется относительно вращающейся системы 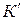со скоростью 
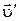, то на нее будет также действовать сила Кориолиса
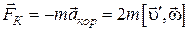, (8)
где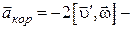 
ускорение Кориолиса.
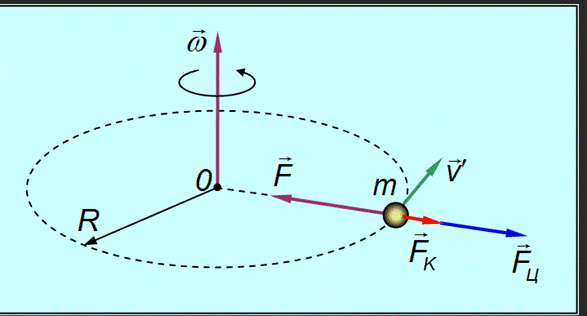
На шарик будут действовать уже две силы инерции: центробежная и сила Кориолиса
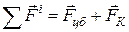
И тогда (6) для второго случая
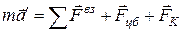(9)
(9) – динамическое уравнение движения частицы в НСО во втором случае.
Примеры проявление сил Кориолиса: при свободном падении все тела отклоняются к востоку от вертикали; летящий снаряд в северном полушарии будет отклоняться к востоку, и к западу – в южном полушарии; у рек, текущих в северном полушарии размывается правый берег, в южном – левый (если смотреть вниз по течению).
Рассмотрим третий случай.
Пусть 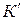-система вращается с постоянной угловой скоростью 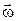вокруг оси, перемещающейся поступательно со скоростью 
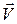и ускорением 
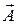относительно 
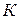-системы.
Этот случай объединяет два первых случая. И тогда уравнение (6)
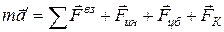. (10)
(10) – динамическое уравнение движения частицы в НСО в третьем случае.
Как видно, даже при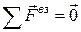 
, частица в НСО будет двигаться с ускорением отличным от нуля 
.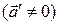